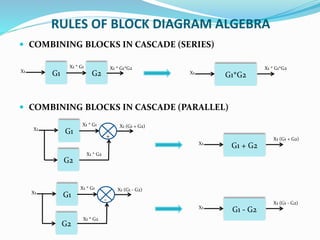
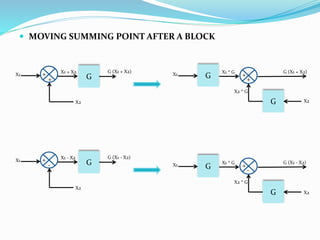
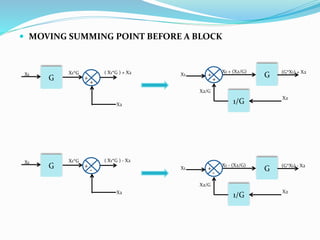
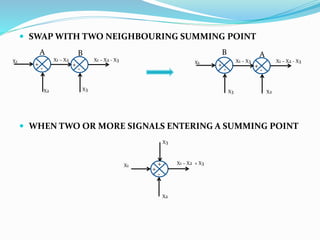
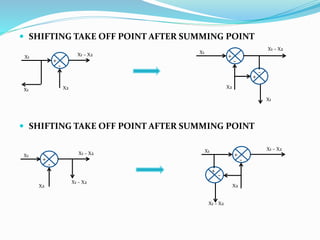
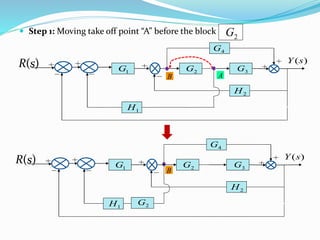
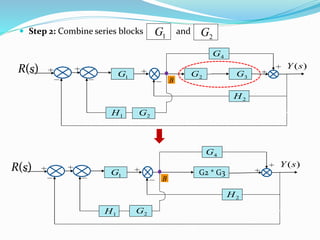
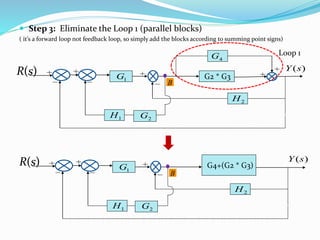
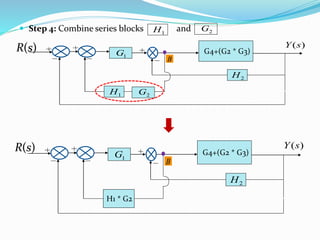
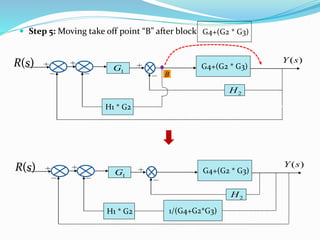
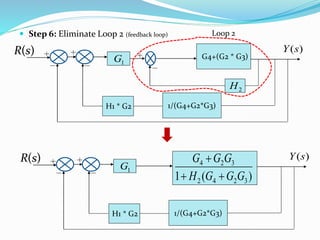
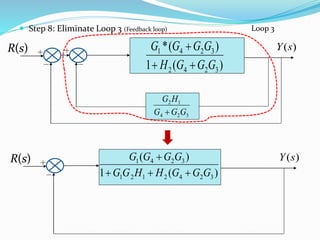
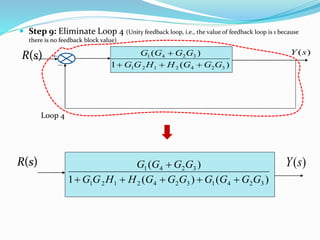
The document outlines rules for block diagram algebra used to derive transfer functions from block diagrams. It describes how to combine blocks in series and parallel, move summing points, eliminate feedback loops, and perform other manipulations. An example problem applies the rules to find the transfer function for a given block diagram in 8 steps, combining and simplifying blocks at each stage.

1. RULES OF BLOCK DIAGRAM ALGEBRA
 COMBINING BLOCKS IN CASCADE (SERIES)
 COMBINING BLOCKS IN CASCADE (PARALLEL)
G1 G2X1
X1 * G1 X1 * G1*G2
G1*G2X1
X1 * G1*G2
G1 + G2X1
X1 (G1 + G2)
X1 * G2
G1
G2
X1
X1 * G1 X1 (G1 - G2)
-
G1 - G2X1
X1 (G1 - G2)
G1
G2
X1
X1 * G1 X1 (G1 + G2)
+
X1 * G2

2.  MOVING SUMMING POINT AFTER A BLOCK
GX1
X1 + X2 G (X1 + X2)
+
X2
+
X2
X2 * G
GX1 X1 * G G (X1 + X2)
+
G
+
GX1
X1 - X2 G (X1 - X2)
-
X2
+
X2 * G
GX1 X1 * G G (X1 - X2)
-
G
+
X2

3.  MOVING SUMMING POINT BEFORE A BLOCK
G
X1 X1*G ( X1*G ) + X2
+
X2
+
X2
X2/G
GX1
X1 + (X2/G) (G*X1) + X2
+
1/G
+
G
X1 X1*G ( X1*G ) - X2
-
X2
+
X2
X2/G
GX1
X1 - (X2/G) (G*X1) - X2
-
1/G
+

4.  MOVING A TAKE OFF POINT AFTER A BLOCK
 MOVING A TAKE OFF POINT BEFORE A BLOCK
GX1
G * X1
X1
X2
GX1
X1 * G
1/G
X1 * G
GX1
G * X1
G*X1
X1
GX1 X1 * G
G
X1 * G

5.  SWAP WITH TWO NEIGHBOURING SUMMING POINT
 WHEN TWO OR MORE SIGNALS ENTERING A SUMMING POINT
-
X3
+X1 X1 – X2
-
X2
+
X1 – X2 - X3
A B
X1 X1 – X3
-
X2
+
X1 – X2 - X3
+
-
AB
X3
+
-
+X1
X2
X3
X1 – X2 + X3

6.  ELIMINATING A FEEDBACK LOOP
G+
+
H
R(s) C(s)
𝐺
1 − 𝐺𝐻
R(s)
C(s)
G-
+
H
R(s) C(s)
𝐺
1 + 𝐺𝐻
R(s)
C(s)

7.  SHIFTING TAKE OFF POINT AFTER SUMMING POINT
 SHIFTING TAKE OFF POINT AFTER SUMMING POINT
X1
+
-
X1
X2
X1 – X2
-
+
-
X1
X2
X1 – X2
+
X1
+
-
X1
X2
X1 – X2
X1 – X2
-
+
-
X1
X2
X1 – X2
+
X1 – X2

8.  Example
 Find the transfer function for the following block diagram.
2G 3G1G
4G
1H
2H
)(sY)(sR

9.  Step 1: Moving take off point “A” before the block
2G
A
2G 3G1G
4G
1H
2H
)(sY)(sR
2G 3G1G
4G
1H
2H
)(sY)(sR
2G
B
B

10.  Step 2: Combine series blocks and
2G1G
2G 3G1G
4G
1H
2H
)(sY)(sR
B
2G
G2 * G31G
4G
1H
2H
)(sY)(sR
B
2G

11.  Step 3: Eliminate the Loop 1 (parallel blocks)
( it’s a forward loop not feedback loop, so simply add the blocks according to summing point signs)
Loop 1
G2 * G31G
4G
1H
2H
)(sY)(sR
B
2G
G4+(G2 * G3)1G
1H
2H
)(sY)(sR
B
2G

12.  Step 4: Combine series blocks and1H 2G
G4+(G2 * G3)1G
1H
2H
)(sY)(sR
B
2G
G4+(G2 * G3)
H1 * G2
1G
2H
)(sY)(sR
B

13.  Step 5: Moving take off point “B” after block G4+(G2 * G3)
G4+(G2 * G3)
H1 * G2
1G
2H
)(sY)(sR
B
G4+(G2 * G3)
H1 * G2
1G
2H
)(sY)(sR
1/(G4+G2*G3)

14.  Step 6: Eliminate Loop 2 (feedback loop)
G4+(G2 * G3)
H1 * G2
1G
2H
)(sY)(sR
1/(G4+G2*G3)
Loop 2
H1 * G2
1G
)(sY)(sR
1/(G4+G2*G3)
)(1 3242
324
GGGH
GGG



15.  Step 7: Combine series blocks , and ,1G )(1 3242
324
GGGH
GGG


H1 * G2
1G
)(sY)(sR
1/(G4+G2*G3)
)(1 3242
324
GGGH
GGG


H1 * G2 1/(G4+G2*G3)
)(sY)(sR
)(1
)(*
3242
3241
GGGH
GGGG


324
12
GGG
HG


16.  Step 8: Eliminate Loop 3 (Feedback loop)
)(sY)(sR
)(1
)(*
3242
3241
GGGH
GGGG


324
12
GGG
HG

)(sY)(sR
)(1
)(
3242121
3241
GGGHHGG
GGGG


Loop 3

17.  Step 9: Eliminate Loop 4 (Unity feedback loop, i.e., the value of feedback loop is 1 because
there is no feedback block value)
)(sY
)(sR
)(1
)(
3242121
3241
GGGHHGG
GGGG


)(sY)(sR
)()(1
)(
32413242121
3241
GGGGGGGHHGG
GGGG


Loop 4

18.  The given block diagram:
 Transfer function for the given block diagram
(from previous slide)
2G 3G1G
4G
1H
2H
)(sY)(sR
)()(1
)(
)(
)(
)(
32413242121
3241
GGGGGGGHHGG
GGGG
sR
sY
sT


