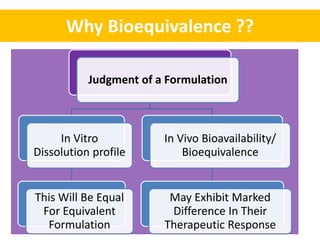
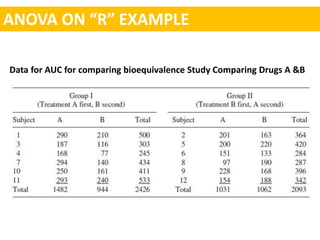
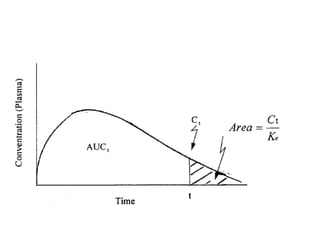
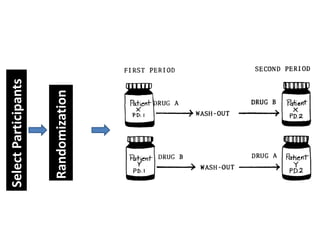
This document discusses bioequivalence and how it is assessed using statistical methods in R. It defines bioequivalence as the comparison of bioavailability between two formulations of the same active ingredient. Key points: - Bioequivalence studies compare pharmacokinetic measures like AUC and Cmax between test and reference drugs. - A common crossover study design involves each subject receiving both drugs on different occasions. 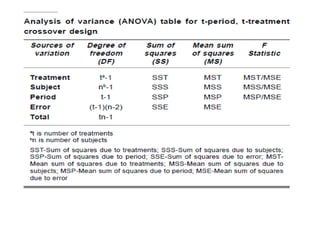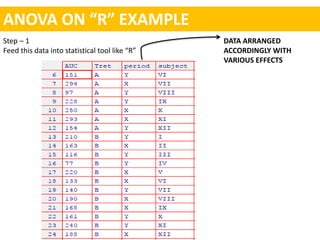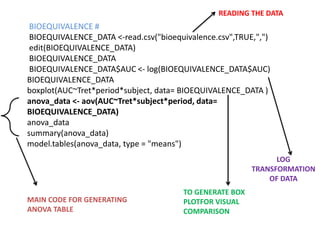- Data are analyzed using ANOVA to separate out variance components and determine equivalence. - The FDA typically uses a 80-125% range for the 90% CI of the ratio of means on log-transformed AUC and Cmax data to determine equivalence. - An example is shown of constructing the 90

1. Bioequivalence: A Statistical Approach
Through “R”
Lavkush Upadhyay
Email- upalavkush@gmail.com

2. What Is Bioequivalence ??
• The comparison of bioavailability of two or more
formulations of same active pharmaceutical
ingredient to be administered by same route.
• The absence of a significant difference in the rate
and extent to which the active ingredient or active
moiety in pharmaceutical equivalents or
pharmaceutical alternatives becomes available at
the site of drug action when administered at the
same molar dose under similar conditions in an
appropriately designed study.

3. Why Bioequivalence ??
Judgment of a Formulation
In Vitro
Dissolution profile
This Will Be Equal
For Equivalent
Formulation
In Vivo Bioavailability/
Bioequivalence
May Exhibit Marked
Difference In Their
Therapeutic Response

4. When &Where Its Used
• Bioequivalence is an important part of an NDA in
which formulation changes have been made during
and after pivotal clinical trials.
• As part of ANDA submissions, in which a generic
product is compared to a marketed, reference
product.
• Bioequivalence studies may also be necessary when
formulations for approved marketed products are
modified.

5. Bioequivalence Study Design
In general, most bioequivalence studies depend on pharmacokinetic
(PK) data( measure of rate and extent of absorption for products, that
provide concentrations of drug in the bloodstream at specified time
points) following administration of the drug.
Pharmacokinetic measures:
 AUC- Area under the blood concentration vs time curve.
 Cmax- Maximum concentration achieved in systemic circulation
 tmax - Time at which maximum concentration achieved , It is a
more direct measure of absorption rate

7. Crossover Design
A crossover design is an experimental design in which each patient
receives both test and the reference. In a typical crossover design, each
subject takes each of the treatments under investigation
on different occasions.
Comparative bioavailability* or bioequivalence studies, in which
two or more formulations of the same drug are compared, are usually
designed as crossover.
studies.
The treatments are typically taken on two
occasions, often called visits or periods
The order of treatment is randomized; that
is, either A is followed by B or B is followed by A, where A and B are the
two treatments.
This design may also be used for the comparison of more than two
treatments.

8. Randomization
SelectParticipants

9. Crossover Design
•Study designs are typically two-period, two-treatment (tttp) crossover studies with
single or multiple (steady state) dosing, fasting or fed.
•The features of the tttp design follow:
1. N subjects recruited for the study are separated into two groups, or two
treatment sequences. N1 subjects take the treatments in the order AB, and N2 in
the order BA, where N1 N2 N. For example, 24 (N) subjects are recruited and 12
(N1) take the Generic followed by the Brand product, and 12 (N2) take the brand
followed by the Generic.
2. After administration of the product in the first period, blood levels of drug are
determined at suitable intervals.
3. A wash-out period follows, which is of sufficient duration to ensure the ‘‘total’’
elimination of the drug given during the first period. An interval of at least nine drug
half-lives should be sufficient to ensure virtually total elimination of the drug. Often, a
minimum of 7 half-lives is recommended.
4. The alternate product is administered in the second period and blood levels
determined

10. Statistical Analysis
The various pharmacokinetic parameters (AUC, Cmax) derived from
the plasma concentration-time curve are subjected to ANOVA in
which the variance is partitioned into components due to subjects,
periods and treatments.
Model for this Design
Let
u = overall mean
Gi = Effect of sequence group i (i 1, 2)
Sik =Effect of subject k in sequence i (k 1, 2.3 … N)
Pj = Effect of period j (j 1, 2)
Tt(i,j)= treatment effect t (t 1, 2) in sequence i and
period j
Yijk = Gi+Sik + Pj + Tt(ij) + eijk

11. ANOVA
• The typical ANOVA for crossover studies will be applied to the
AUC data to illustrate the procedure used to analyze the
experimental results. In these analyses, the residual error term is
used in statistical computations, e.g., to construct confidence
intervals. An analysis of variance (ANOVA) is computed for each
parameter based on the model.
• The analysis removes some effects from the total variance to
obtain a more ‘‘efficient’’ or pure estimate of the error term. It is
the error term, or estimate of the within subject variability
(assumed to be equal for both products in this analysis), that is
used to assess the equivalence of the parameter being analyzed.

12. ANOVA ON “R”
Anova on “R” can be performed using following function on “R”
aov(formula, data = NULL, projections = FALSE, qr = TRUE,
contrasts = NULL, ...)
Example:
aovtab <- aov(AUC~period+Tret+subject,data = poo)
summary(aovtab)

14. Log Transformed Data
Logarithmic transformation of bioequivalence
parameters
Bioequivalence studies measure and compare statistically AUC, Cmax
and Tmax of the formulations. In case of AUC and Cmax, the regulatory
authorities recommend that they should be logarithmically transformed
before further statistical analysis.
The log transform appears to be more natural when our interest is in the
ratio of the
product outcomes. The antilog of the difference of the average results
gives the ratio directly.

15. Bioequivalence Range
The present FDA requirement for equivalence is based on product
ratios using a symmetric 90% confidence interval for the difference
of the average parameters, after a log transformation.
For a broad range of drugs, the US FDA has used a range
of 80-120% for the 90% C.I. of the ratio of the product averages
as the standard equivalence criterion
When log-transformed data are used in the analysis of AUC
and Cmax, it is recommended to use 80-125% for the 90% C.I.
of the ratio of the product averages as the standard equivalence
criterion.

16. Data for AUC for comparing bioequivalence Study Comparing Drugs A &B
ANOVA ON “R” EXAMPLE

17. Step – 1
Feed this data into statistical tool like “R”
DATA ARRANGED
ACCORDINGLY WITH
VARIOUS EFFECTS
ANOVA ON “R” EXAMPLE

18. BIOEQUIVALENCE #
BIOEQUIVALENCE_DATA <-read.csv("bioequivalence.csv",TRUE,",")
edit(BIOEQUIVALENCE_DATA)
BIOEQUIVALENCE_DATA
BIOEQUIVALENCE_DATA$AUC <- log(BIOEQUIVALENCE_DATA$AUC)
BIOEQUIVALENCE_DATA
boxplot(AUC~Tret*period*subject, data= BIOEQUIVALENCE_DATA )
anova_data <- aov(AUC~Tret*subject*period, data=
BIOEQUIVALENCE_DATA)
anova_data
summary(anova_data)
model.tables(anova_data, type = "means")
READING THE DATA
LOG
TRANSFORMATION
OF DATA
TO GENERATE BOX
PLOTFOR VISUAL
COMPARISON
MAIN CODE FOR GENERATING
ANOVA TABLE

19. ANOVA TABLE
SEPERATION
OF VARIANCE
AMONG
VARIOUS
EFFECTS
STANDARD ERROR/ RESIDUAL
This if further used for the construction of confidence
interval and hypothesis test

20. Averages ln transformed values of data

21. Bioequivalence Range
The present FDA requirement for equivalence is based on product
ratios using a symmetric 90% confidence interval for the difference
of the average parameters, after a log transformation.
For a broad range of drugs, the US FDA has used a range
of 80-120% for the 90% C.I. of the ratio of the product averages
as the standard equivalence criterion
When log-transformed data are used in the analysis of AUC
and Cmax, it is recommended to use 80-125% for the 90% C.I.
of the ratio of the product averages as the standard equivalence
criterion.

22. Constructing 90 % confidence interval of log transformed data.
The difference of the logarithms is equivalent to the logarithm of the ratio
[i.e., log A-logB = log (A/B)].
Formula for calculating confidence interval = log (A/B) ± t-value√SE/(1/N1 + 1/N2)
The averages In values for the test and standard products are
A = 5.29751
B = 5.07778
A –B = 5.29751 – 5.0778 = 0 21973
SE(computed from anova table ) = 0.045
t- value for 90% confidence interval = 1.81
N1 = 12
N2 = 12
CI = log (A/B) ± t-value√SE/(1/N1 + 1/N2)
= 0.21973±1.81 √ 0.045/ 6
= 0.06298 to 0.37648

23. REFRENCES
• Pharmaceutical Statistics, practical and clinical
applications, Fifth edition.
• CDSCO guidelines for Bioavailability & Bioequivalence
2005
• Bioequivalence: An overview of statistical concepts ,S.
Rani, A. Pargal, Indian J Pharmacol | August 2004 | Vol
36 | Issue 4 | 209-216
By- Lavkush Upadhyay
Email- upalavkush@gmail.com
for further and advanced topics on pharmaceutical statistics contact on
above mail id.