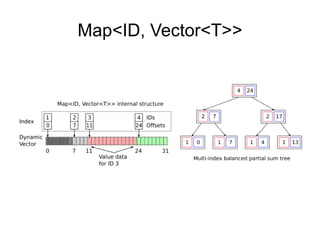
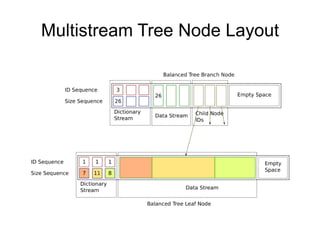
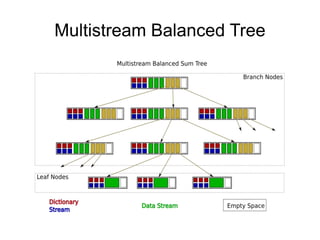
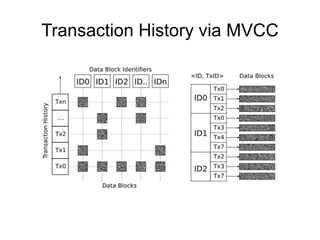
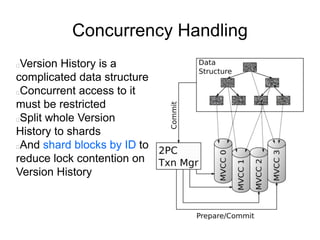
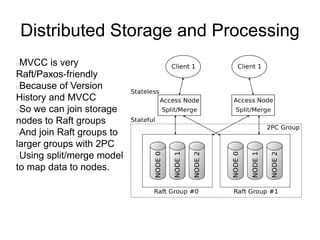
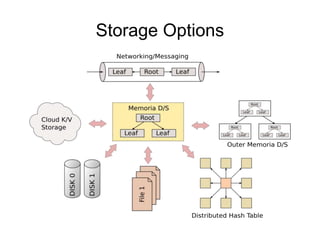
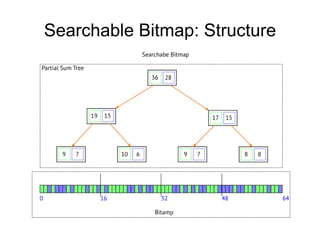
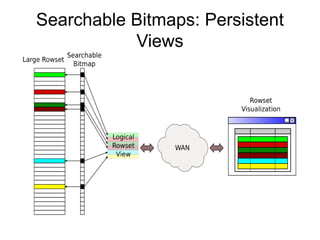
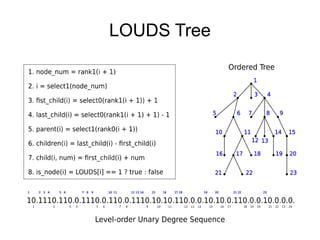
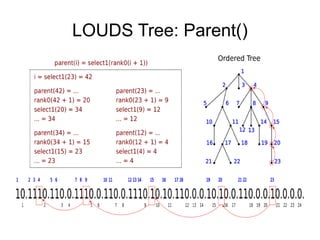
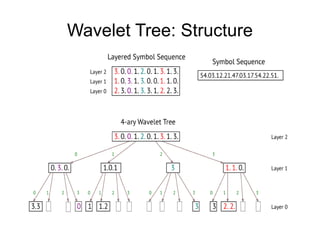
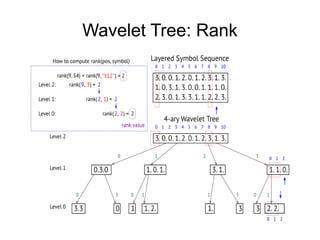
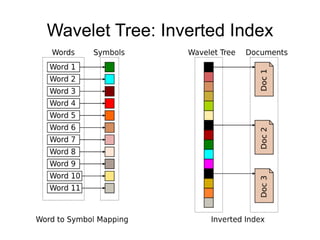
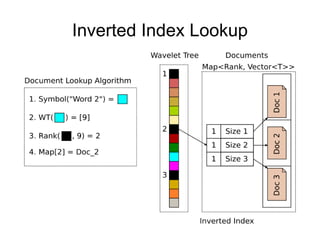
The document discusses advanced non-relational schemas for handling big data, emphasizing the importance of data structures over algorithms in programming. It introduces various data structures such as dynamic vectors, balanced trees, and searchable bitmaps while explaining their time complexities and operations. Additionally, it explores multi-version concurrency control (MVCC) for managing versions of data blocks and enhancing concurrency in distributed storage environments.

1. Advanced Non-Relational Schemas
For Big Data
by Victor Smirnov

2. “Data dominates. If you've chosen the right data
structures and organized things well, the
algorithms will almost always be self-evident. Data
structures, not algorithms, are central to
programming. (See Brooks p.102).”- Rob Pike,
Notes on Programming in C, 1989

3. What If You Need...
Dynamic Vector
Searchable Bitmap
File System
Compact Inverted Index
Suffix Tree/Suffix Array
Version History
Name Your Specific Problem...

4. Non-Relational Schema
Is just a data structure
That uses some Memory Model
Typically, Key->Value mapping
Where Key is an Integer ID
And Value is an arbitrary array of a limited size or
memory block
It's assumed that operations on memory blocks
are atomic.

5. Partial (Prefix) Sums Tree
Given a sequence of S[0, N) = s0...sn-1 of non-
negative integers
Sum(i) returns X = s0+s1+...+si.
FindLT(X) returns max position i that Sum(i) < X
FindLE(X) is the same, but Sum(i) <= X
We can also define range versions of Sum(i, j) and
FindLT(j, X)
All operations perform in O(log N) time.

6. Packing Perfect Balanced Tree into an Array

7. Some Performance Bits

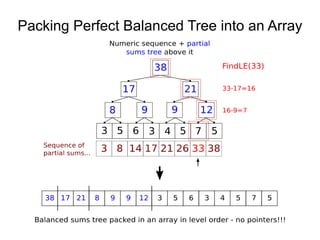
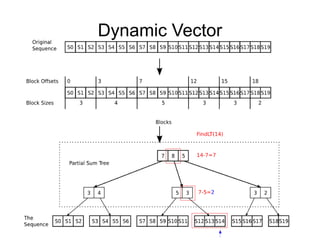
8. Dynamic Vector
An ordered sequence of elements (bytes,
integers, strings) of size N
Acess(i) is O(log N)
Insert(i, value) is O(log N)
Delete(i) is O(log N)
We can also define batch operations:
Insert(i, value[])
Delete(i, j)
Split(i); Merge(AnotherVector);...

9. Dynamic Vector

10. Dynamic Vector Operations
FindLT(i) returns the B where i bounds and offset
j in the block B for i
Acces(i) is O(log N)
Insert(i, value) and Delete(i) are also O(log N)
because the tree is balanced.

11. File System: Map<ID, Vector<T>>
Maps ID to Vector<T>
Merge all values into one large Dynamic Vector,
in ID order
Create separate “index” sequence from pairs <ID,
Offset> in ID order
We can represent this “index” sequence as two
partial sums tree, for ID and for Offset
We can merge both these trees to one because
they have exactly the same structure: multi-index
balanced partial sums tree.

12. Map<ID, Vector<T>>

13. Sharing Tree Structures
Tree structure sharing saves both space and
time: SPMD principle (single program, multiple
data)
We can align partial sum trees with different
structures using interpolation (padding with
zeroes)
We can merge index and data streams (index
and data) of Map<ID, Vector<T>> in one multi-
stream tree.
Merging the trees, we will try to fit index pairs and
corresponding data into the same leaf node of
multi-stream tree.

14. Multistream Tree Node Layout

15. Multistream Balanced Tree

16. ACID
Atomic block operations are not enough
Even simple tree update affects several blocks
So, ACID is mandatory for advanced non-
relational schemas
We can get ACID for free with Multi-Version
Concurrency Control (MVCC)
We need Version History over data blocks
Where each each transaction is a version.

17. Transaction History via MVCC

18. Version History Implementation
Version History maps pair <ID, Version> to an ID
of real data block for that version and given ID
We have Map<ID, Vector<Version, ID>>
We can turn it to Version History by sorting each
Vector<Version, ID> (less sapce, slower)
Or by creating additional partial sums tree index
on top of it (more space, but much faster)
We can do it in just one multi-stream balanced
tree
MVCC requires some other data structures but
they can be designed by analogy.

19. Concurrency Handling
Version History is a
complicated data structure
Concurrent access to it
must be restricted
Split whole Version
History to shards
And shard blocks by ID to
reduce lock contention on
Version History

20. Distributed Storage and Processing
MVCC is very
Raft/Paxos-friendly
Because of Version
History and MVCC
So we can join storage
nodes to Raft groups
And join Raft groups to
larger groups with 2PC
Using split/merge model
to map data to nodes.

21. Storage Options

22. Bonus Slides

23. Searchable Bitmaps
rank1(n) = number of ones in [0, n)
select1(i) = position of i-th 1 in the bitmap
rank0(n) = number of zeroes in [0, n)
select0(i) = position of i-th 0 in the bitmap

24. Searchable Bitmap: Structure

25. Searchable Bitmaps: Persistent
Views

26. LOUDS Tree

27. LOUDS Tree: Parent()

28. Wavelet Tree
Searchable sequence [0...N) for large alphabets
Rank(i, s) returns number of symbols s in [0, i)
Select(k, s) returns position i of k-th symbol s
Insert(i, s), Delere(i), Access(i) – insert, remove
and access the symbol at position i respectively
All these operations have O(log N) time
complexity
By mapping numbers to symbols we can perform
the following lookup operations: >, >=, <, <=, <> in
O(log N) time.

29. Wavelet Tree: Structure

30. Wavelet Tree: Rank

31. Wavelet Tree: Inverted Index

32. Inverted Index Lookup

33. Thanks!
More details are at:
http://bit.ly/1D4cj21