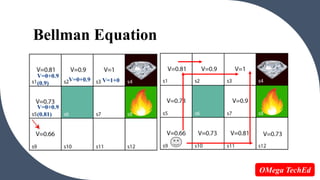
The Bellman equation is used to calculate the value of states in reinforcement learning and dynamic programming. It defines the value of a state based on the expected rewards from being in that state plus the discounted value of the next state. The document provides an example of using the Bellman equation to calculate the value of different states in an environment by starting from the final state and working backwards. Key elements of the Bellman equation include the action, next state, reward, and discount factor for weighing future rewards.

1. Bellman’s Equation
Reinforcement Learning
OMega TechEd

2. Bellman Equation
The Bellman equation was introduced by the Mathematician Richard
Ernest Bellman in the year 1953, and hence it is called as a Bellman
equation. It is associated with dynamic programming and used to calculate
the values of a decision problem at a certain point by including the values of
previous states.
It is a way of calculating the value functions in dynamic programming or
environment that leads to modern reinforcement learning.
2
OMega TechEd

3. Key elements in Bellman equation
•Action performed by the agent is referred to as "a"
•State occurred by performing the action is "s."
•The reward/feedback obtained for each good and bad action is "R."
•A discount factor is Gamma "γ.“: determines how much the agent cares about
rewards in the distant future relative to those in the immediate future. It has a
value between 0 and 1. Lower value encourages short–term rewards
while higher value promises long-term reward.
3
OMega TechEd

4. The Bellman equation
V(s) = max [R(s,a) + γV(s`)] Where,
• State(s): current state where the agent is in the environment.
• Next State(s’): After acting(a) at state(s) the agent reaches s’.
• Value(V): Numeric representation of a state which helps the agent to find
its path. V(s) here means the value of the state s.
• R(s): reward for being in the state s.
• R(s,a): reward for being in the state and performing an action a.
4
OMega TechEd

5. For 1st block
V(s3) = max [R(s,a) + γV(s`)], here V(s')= 0 because there is no further state
to move.
V(s3)= max[R(s,a)]=> V(s3)= 1.
5
Using the Bellman equation, we
will find value at each state of the
given environment. We will start
from the block, which is next to
the target block.
OMega TechEd

6. For 2nd block
V(s2) = max [R(s,a) + γV(s`)],
here γ= 0.9(lets), V(s')= 1, and R(s, a)= 0, because there is no reward at this
state.
V(s2)= max[0.9(1)]=> V(s2) =0.9
6
1
OMega TechEd

7. For 3rd block
V(s1) = max [R(s,a) + γV(s`)],
here γ= 0.9(lets), V(s')= 0.9, and R(s, a)= 0, because there is no reward at this
state also.
V(s1)= max[0.9(0.9)]=> V(s1) =0.81
7
1
0.9
OMega TechEd

8. For 4th block
V(s5) = max [R(s,a) + γV(s`)],
here γ= 0.9(lets), V(s')= 0.81, and R(s, a)= 0, because there is no reward at this
state also.
V(s5)= max[0.9(0.81)]=> V(s5) =0.73
8
1
0.9
0.81
OMega TechEd

9. For 5th block
V(s9) = max [R(s,a) + γV(s`)],
here γ= 0.9(lets), V(s')= 0.73, and R(s, a)= 0, because there is no reward at this
state also.
V(s9)= max[0.9(0.73)]=> V(s4) =0.66
9
1
0.9
0.81
0.73
OMega TechEd

10. Bellman Equation
10
V=1+0
V=0+0.9
V=0+0.9
(0.9)
V=0+0.9
(0.81)
OMega TechEd

11. Applications
11
Business Gaming
Recommendation
System
Robotics Finance Control
OMega TechEd

12. Thank you
Reference:
Artificial Intelligence: A Modern Approach, 3rd ed.
Stuart Russell and Peter Norvig
https://www.javatpoint.com/reinforcement-learning
Join Telegram channel for AI notes. Link is in the description.
OMega TechEd