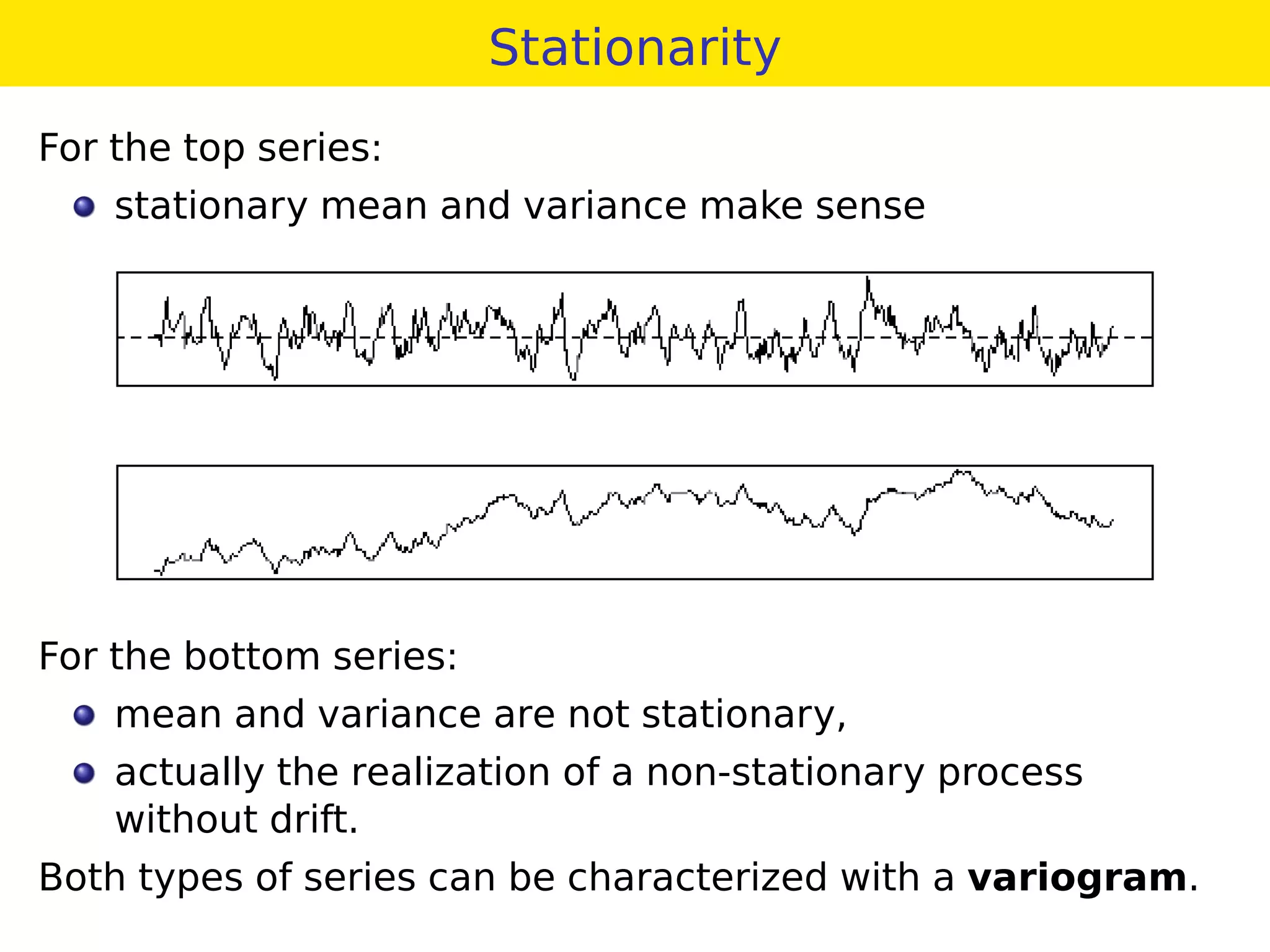
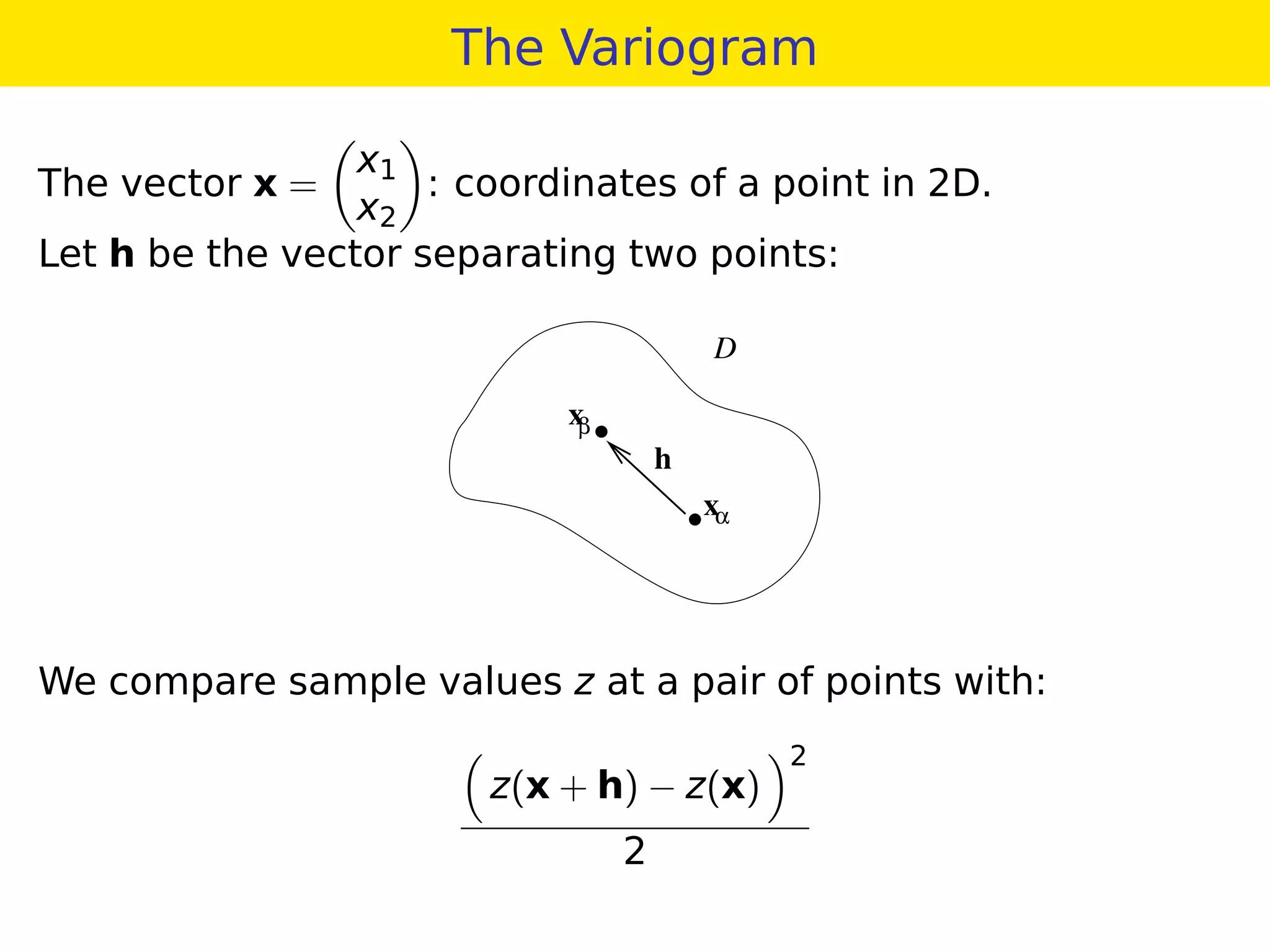
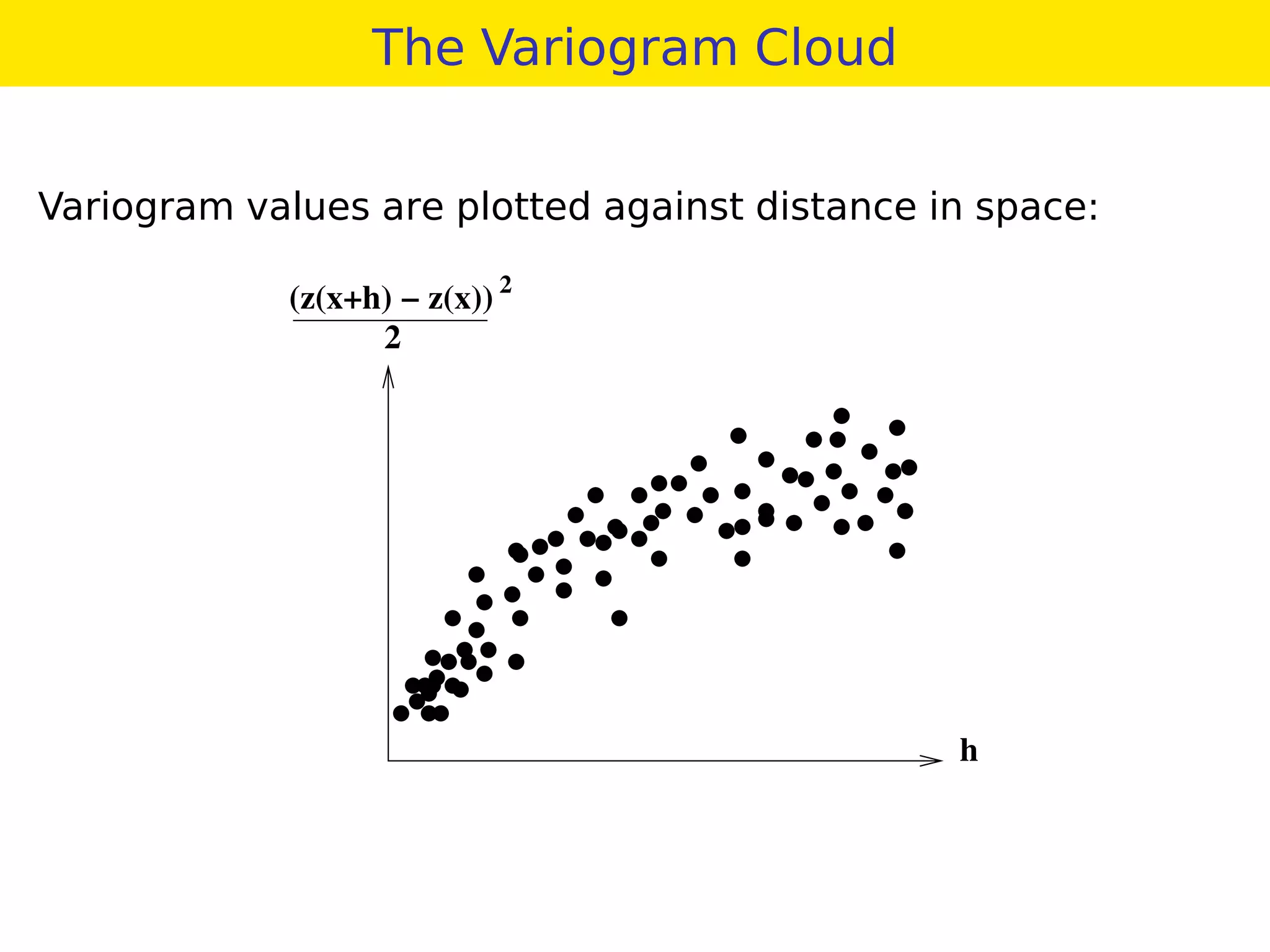
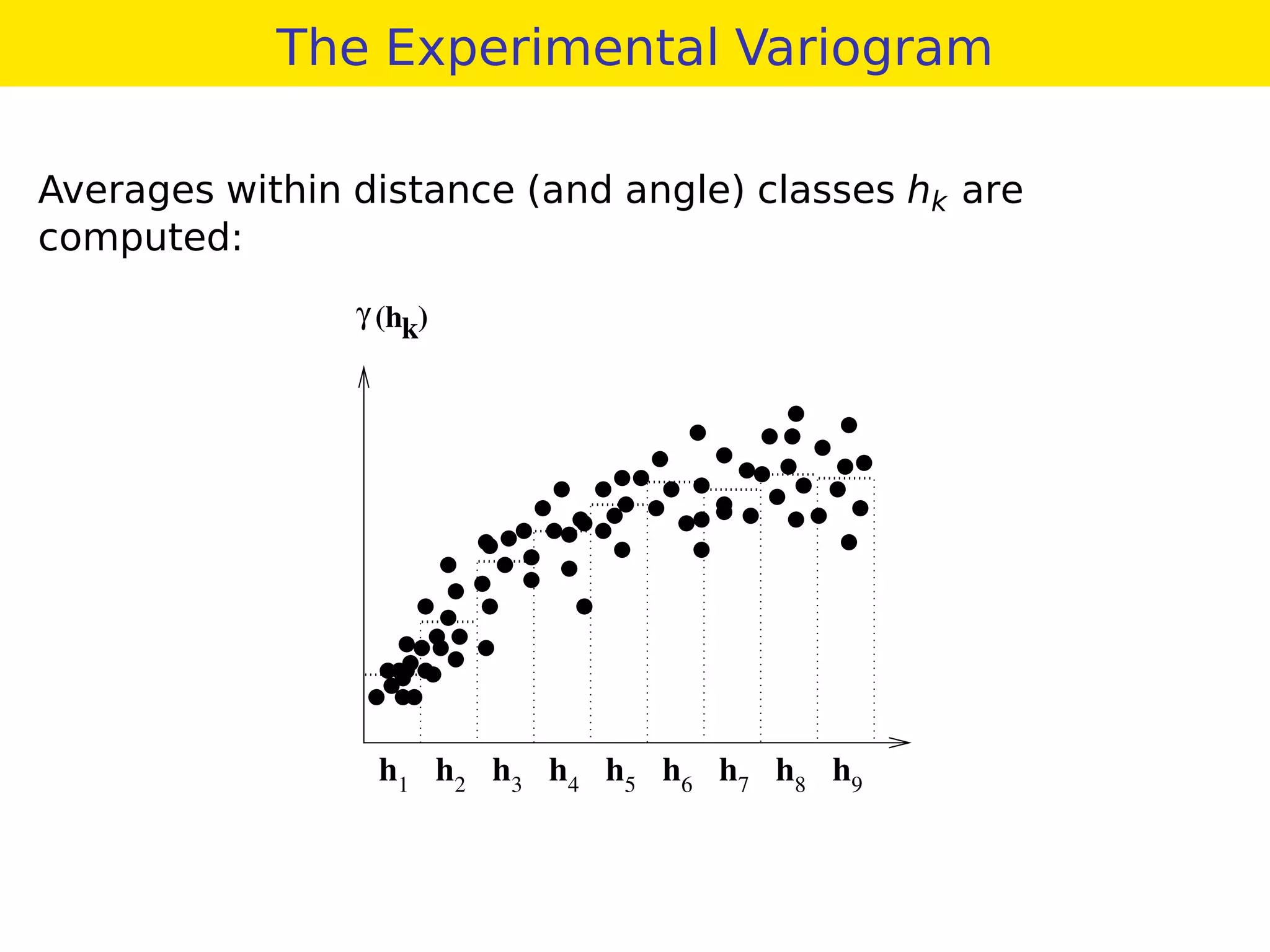
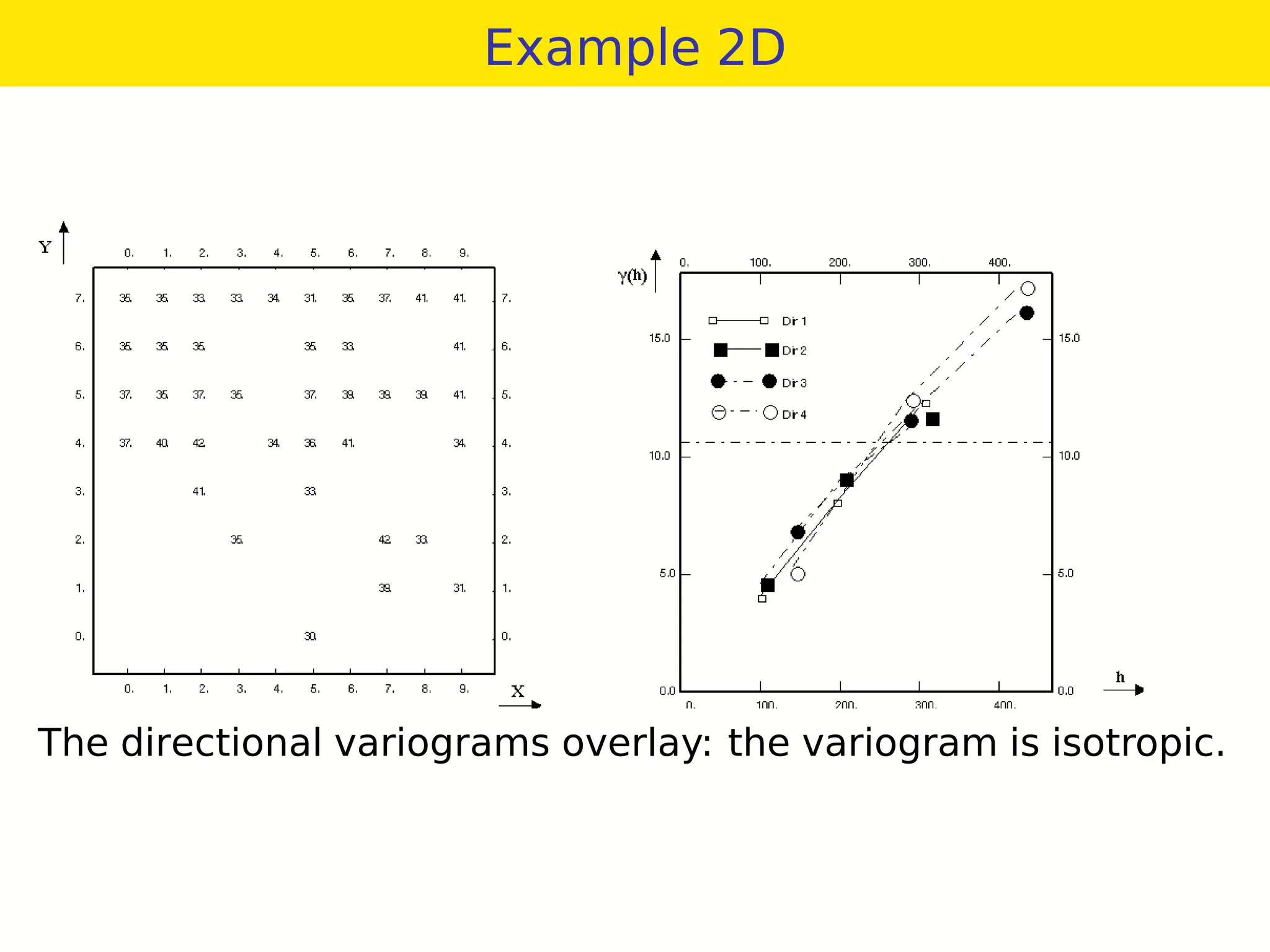
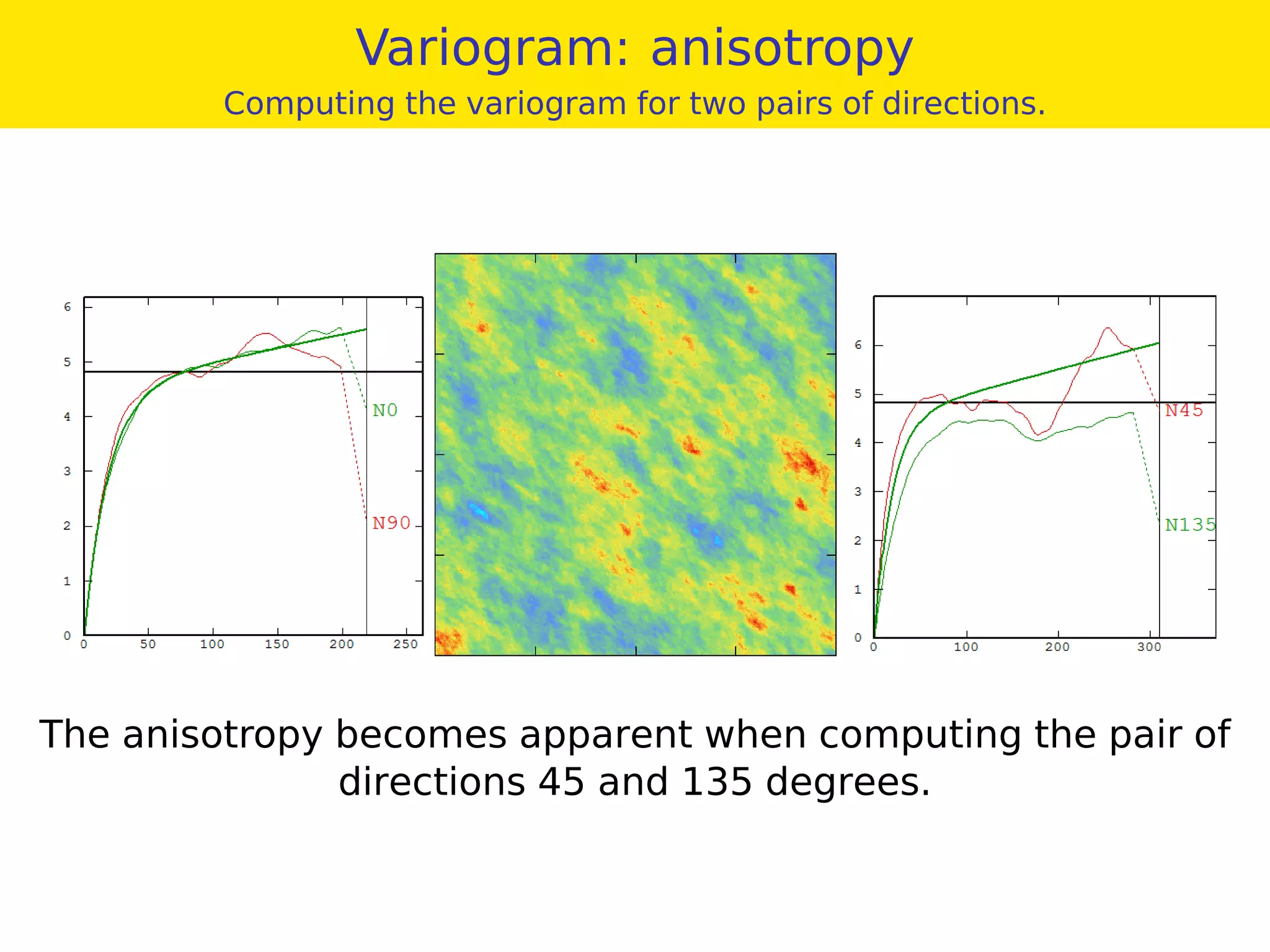
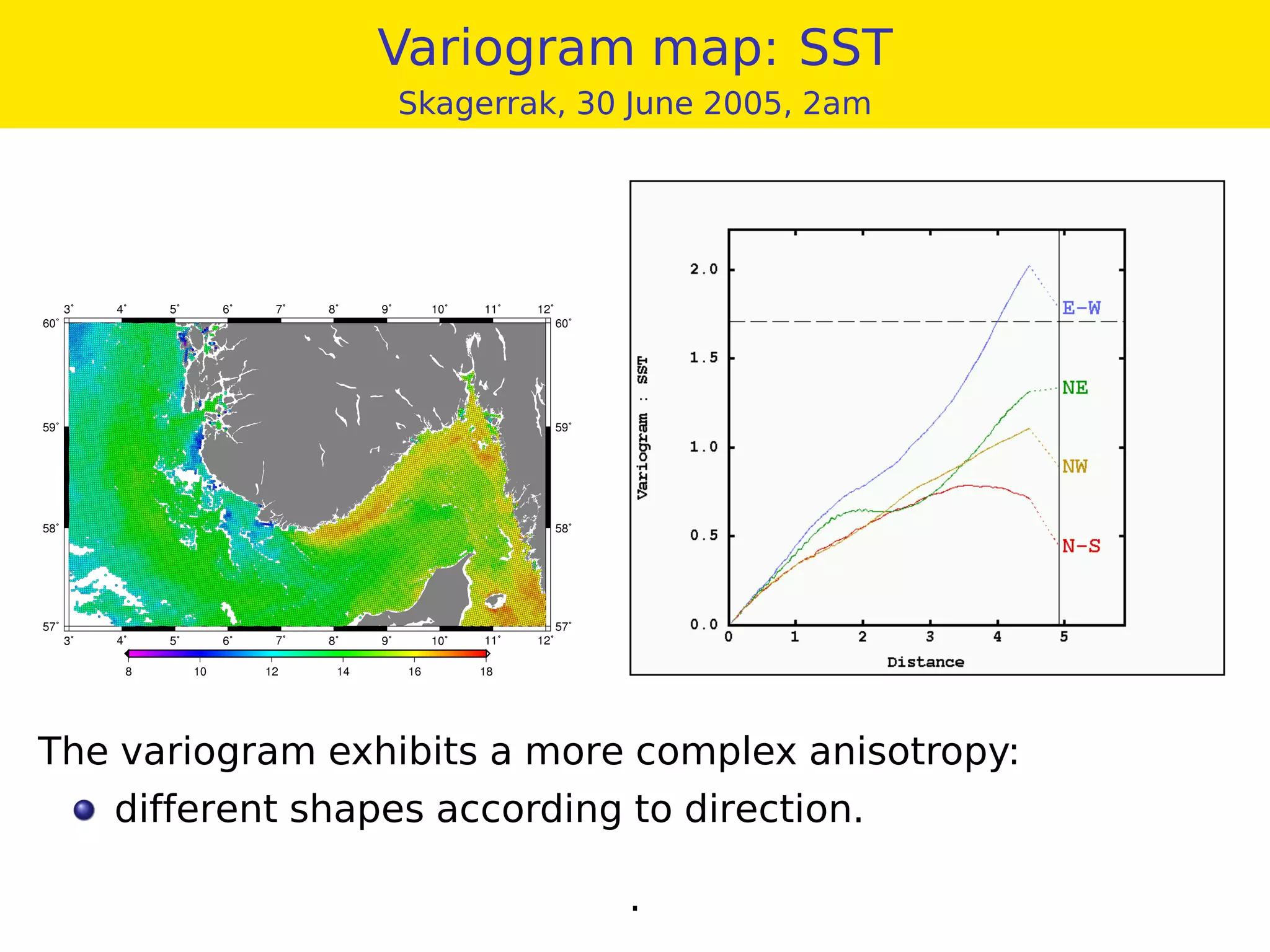
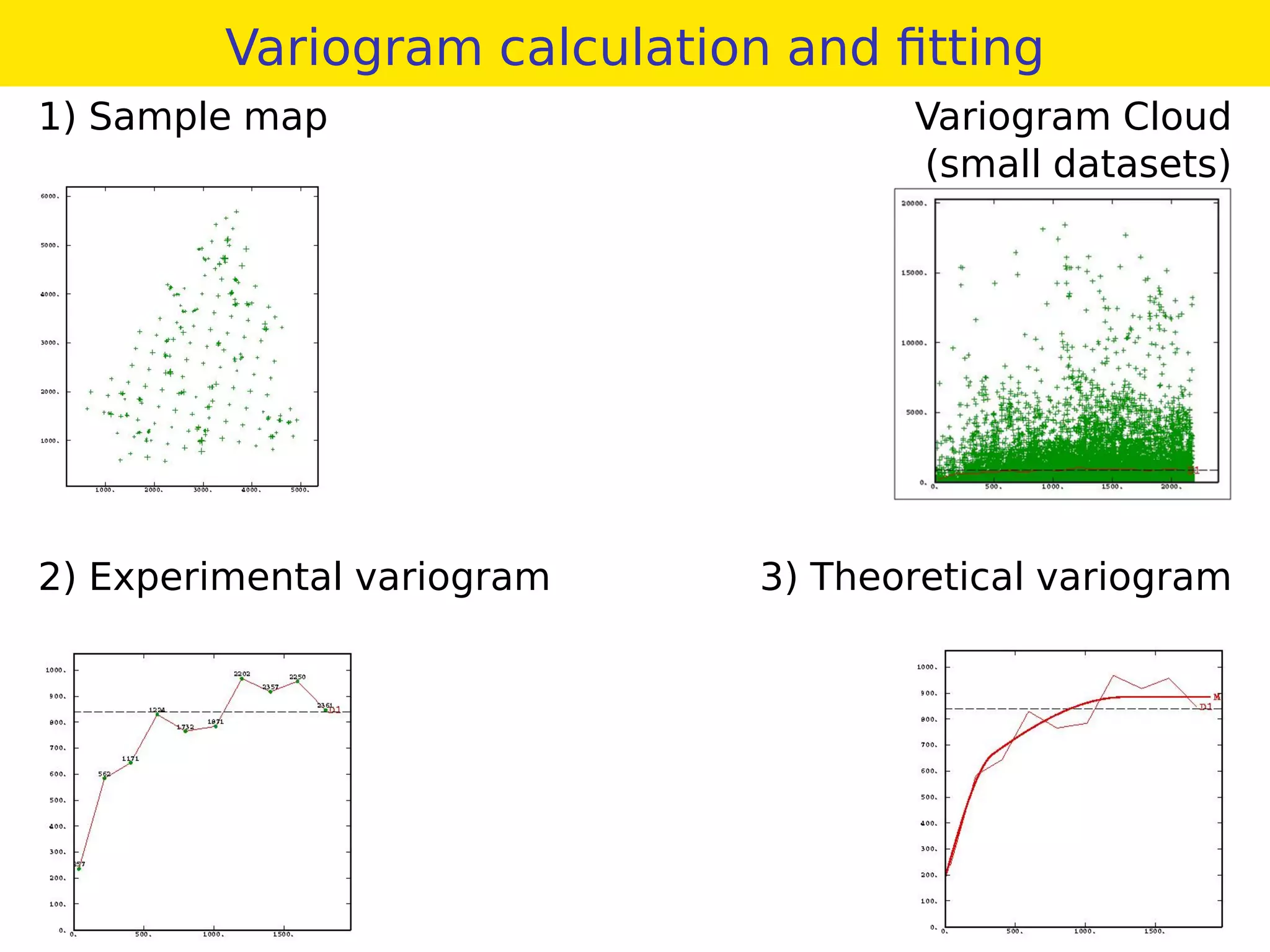
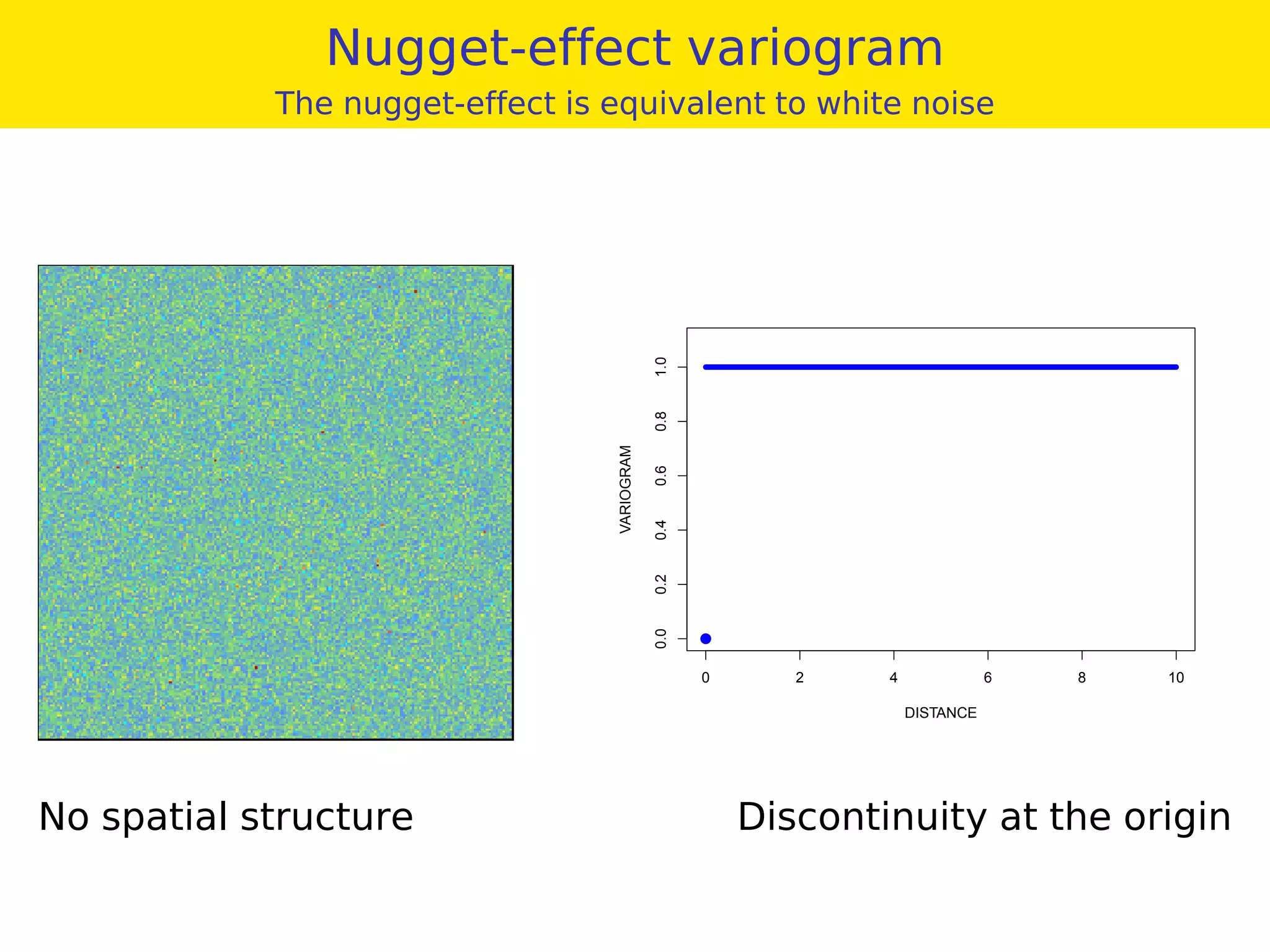
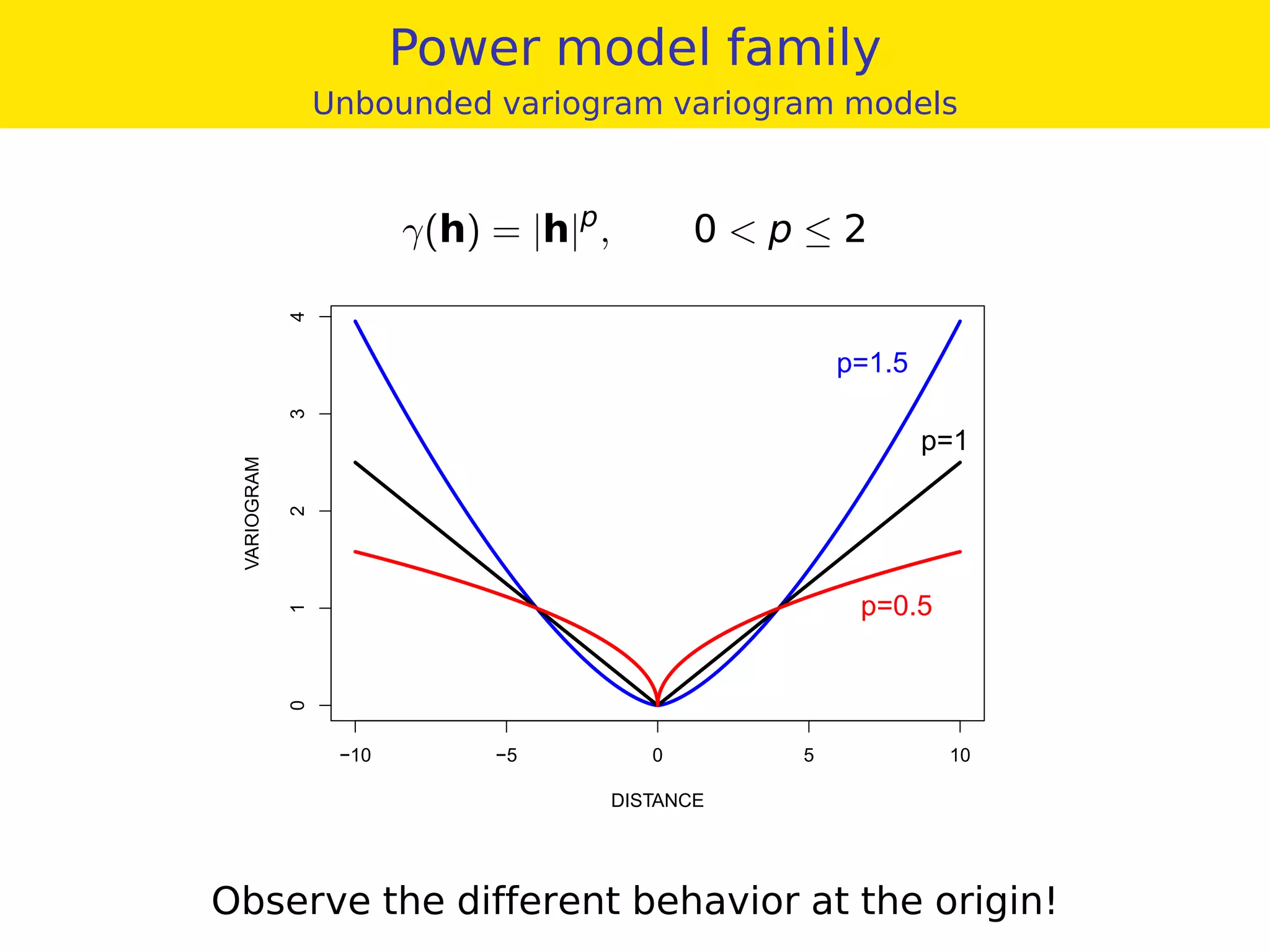
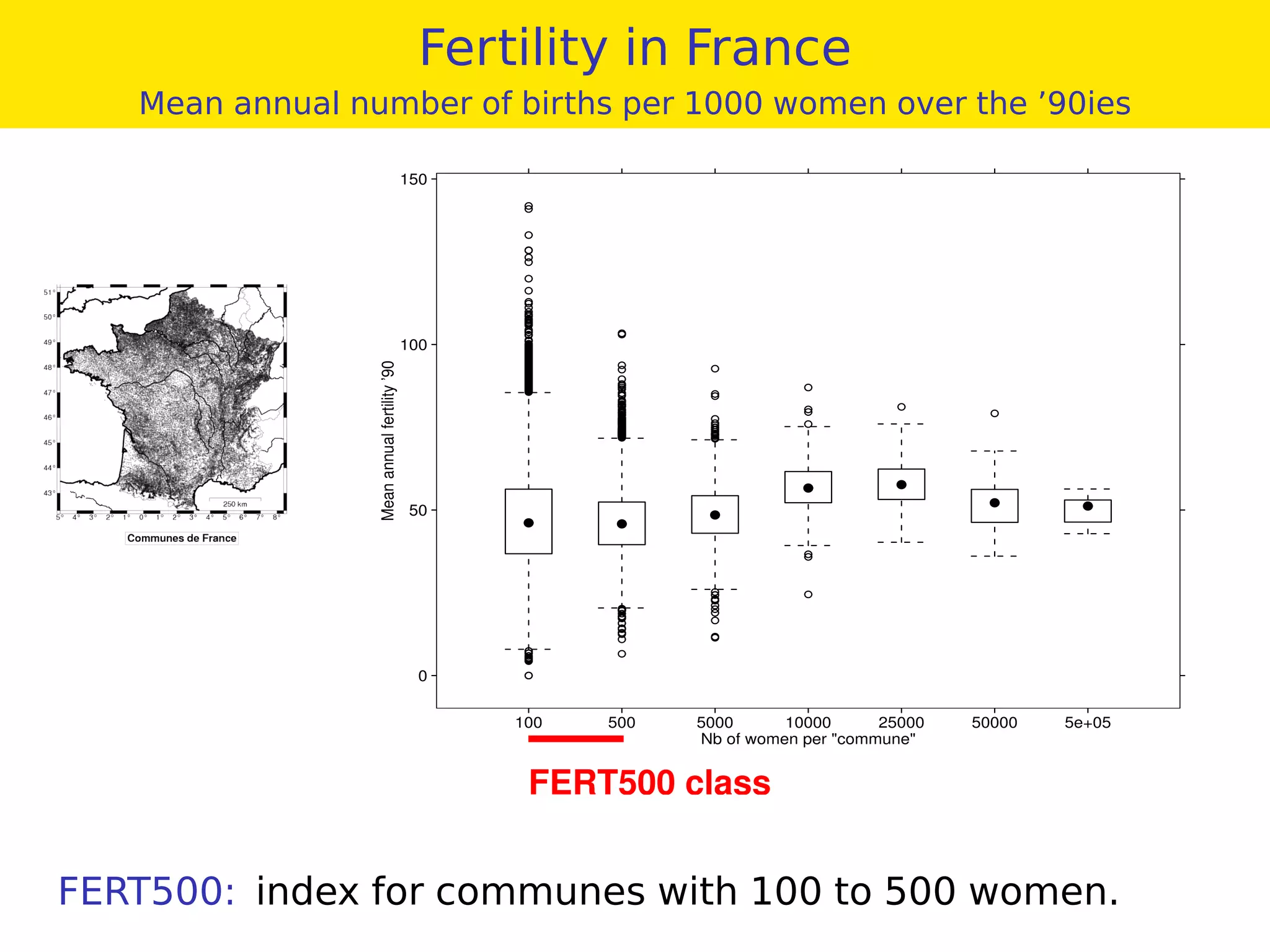
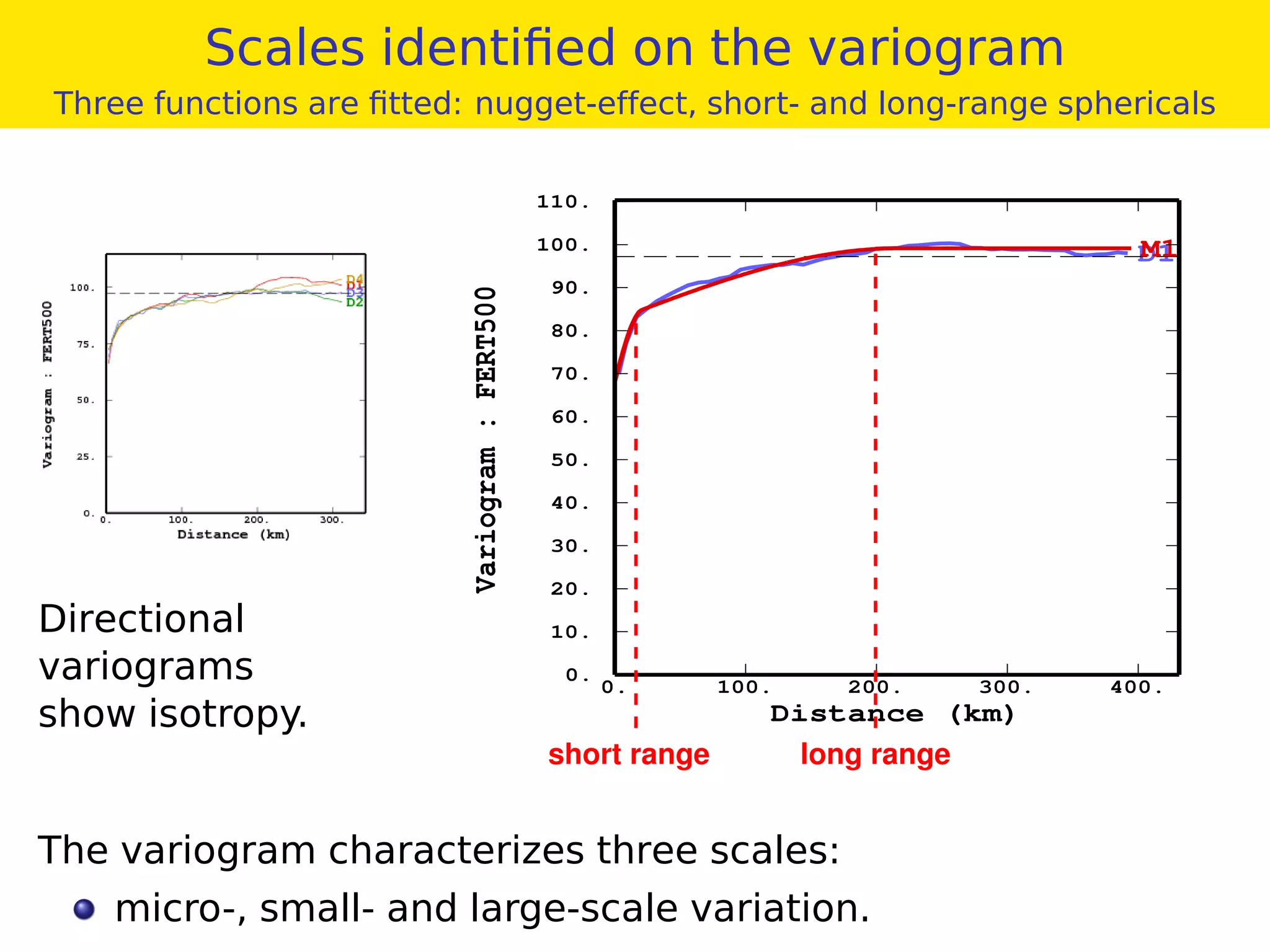
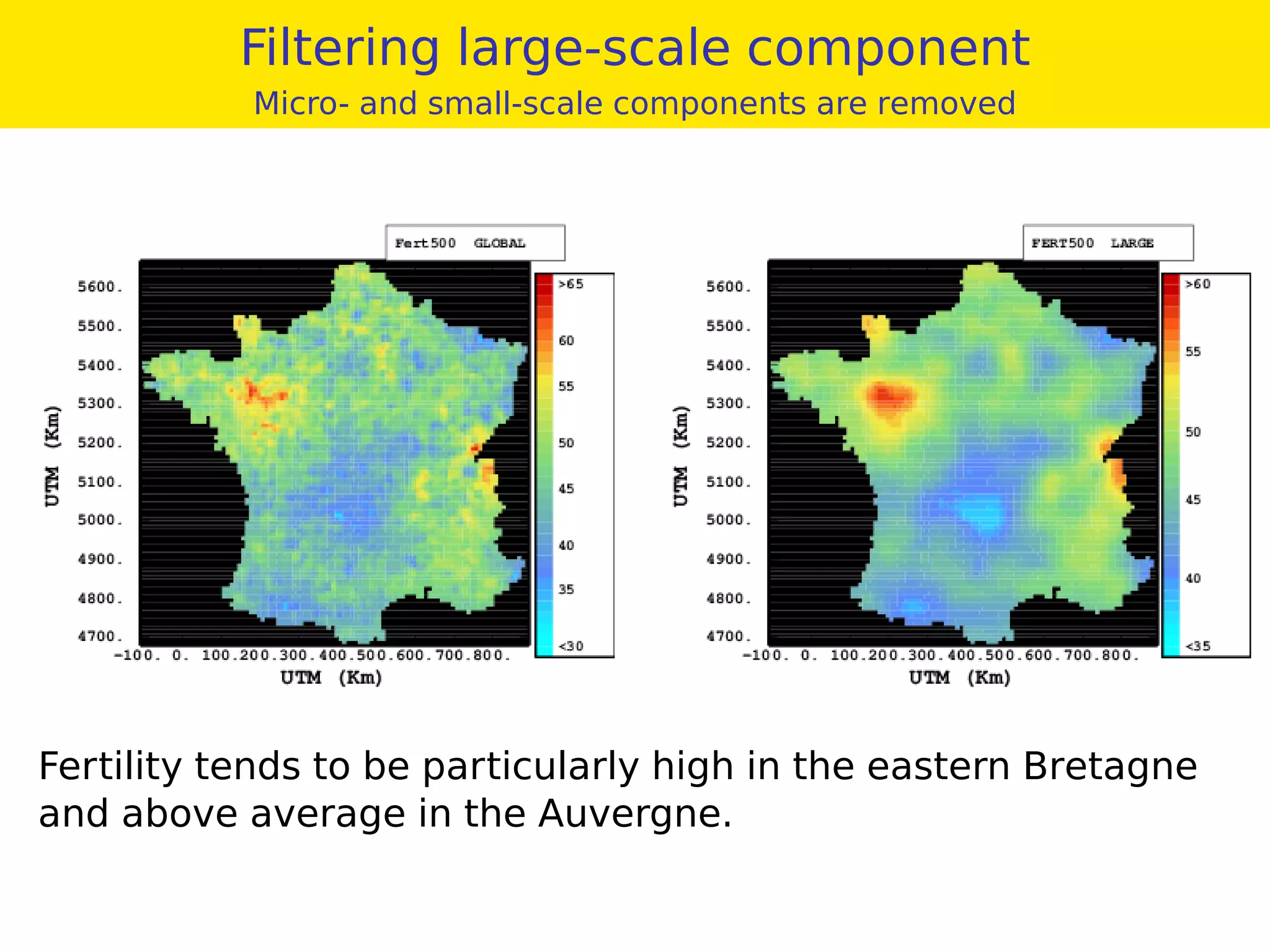
This document provides an overview of geostatistics and variogram analysis. It discusses how the variogram describes the spatial correlation of a phenomenon through parameters like the nugget effect and range. Experimental variograms are calculated from data and theoretical models like spherical, exponential, and power models are fitted. The variogram can identify different correlation scales through nested models. Components at different scales can be extracted through kriging. As an example, fertility data from France is analyzed to filter its large-scale spatial structure.

1. Basics in Geostatistics 1
Geostatistical structure analysis:
The variogram
Hans Wackernagel
MINES ParisTech
NERSC • April 2013
http://hans.wackernagel.free.fr

2. Basic concepts
Geostatistics
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 2 / 32

3. Geostatistics
Geostatistics is an application of
the theory of Regionalized Variables
to the problem of predicting spatial
phenomena.
Georges Matheron (1930-2000)
Note: the regionalized variable (reality) is viewed as a realization
of a random function, which is a collection of random variables.
Geostatistics has been applied to:
geology and mining since the ’50ies,
natural phenomena since the ’70ies.
It (re-)integrated mainstream statistics in the ’90ies.

4. Geostatistics
Geostatistics is an application of
the theory of Regionalized Variables
to the problem of predicting spatial
phenomena.
Georges Matheron (1930-2000)
Note: the regionalized variable (reality) is viewed as a realization
of a random function, which is a collection of random variables.
Geostatistics has been applied to:
geology and mining since the ’50ies,
natural phenomena since the ’70ies.
It (re-)integrated mainstream statistics in the ’90ies.

5. Concepts
Variogram: function describing the spatial correlation of a
phenomenon.

6. Concepts
Variogram: function describing the spatial correlation of a
phenomenon.
Kriging: linear regression method for estimating values at
any location of a region.
Daniel G. Krige (1919-2013)

7. Concepts
Variogram: function describing the spatial correlation of a
phenomenon.
Kriging: linear regression method for estimating values at
any location of a region.
Daniel G. Krige (1919-2013)
Conditional simulation: simulation of an ensemble of
realizations of a random function,
conditional upon data — for non-linear estimation.

8. Stationarity
For the top series:
stationary mean and variance make sense
For the bottom series:
mean and variance are not stationary,
actually the realization of a non-stationary process
without drift.
Both types of series can be characterized with a variogram.

9. Structure analysis
Variogram
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 6 / 32

10. The Variogram
The vector x =
x1
x2
: coordinates of a point in 2D.
Let h be the vector separating two points:
G
G
h
D
x
x
β
α
We compare sample values z at a pair of points with:
z(x + h) − z(x)
2
2

11. The Variogram Cloud
Variogram values are plotted against distance in space:
GG
GG
GG
G
GG G
GGG
GG
G G G
G
G
G
G G
G
G G
GG
G
G
G
G
G
G G
G
G
G
G
G
G
G
G
G
G
G
G
GGG
G
G
G
G
G
G
G GG
GG
G
G
G
G
G
G G
G
G
G
G
G G
G
G
G
h
(z(x+h) − z(x))
2
2

12. The Experimental Variogram
Averages within distance (and angle) classes hk are
computed:
GG
GG
GG
G
GG G
GGG
GG
G G G
G
G
G
G G
G
G G
GG
G
G
G
G
G
G G
G
G
G
G
G
G
G
G
G
G
G
G
GGG
G
G
G
G
G
G
G GG
GG
G
G
G
G
G
G G
G
G
G
G
G G
G
G
G
h hh h h h h hh1 2 3 4 5 6 7 8 9
γ k(h )

13. The Theoretical Variogram
A theoretical model is fitted:
γ
h
(h)

14. The theoretical Variogram
Variogram: average of squared increments for a spacing h,
γ(h) =
1
2
E Z(x+h) − Z(x)
2
Properties
- zero at the origin γ(0) = 0
- positive values γ(h) ≥ 0
- even function γ(h) = γ(−h)
The variogram shape near the origin is linked to the
smoothness of the phenomenon:
Regionalized variable Behavior of γ(h) at origin
smooth ←→ continuous and differentiable
rough ←→ not differentiable
speckled ←→ discontinuous

15. Structure analysis
The empirical variogram
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 12 / 32

16. Empirical variogram
Variogram: average of squared increments for a class hk,
γ (hk) =
1
2 N(hk)
xα−xβ∈hk
(Z(xα) − Z(xβ))2
where N(hk) is the number of lags h = xα−xβ within
the distance (and angle) class hk.

17. Example 1D
Transect :

18. Example 1D
Transect :
γ (1) =
1
2 × 9
(02
+ 22
+ 02
+ 12
+ 32
+ 42
+ 22
+ 42
+ 02
) = 2.78
γ (2) =
1
2 × 8
(22
+ 22
+ 12
+ 22
+ 12
+ 62
+ 62
+ 42
) = 6.38

19. Example 1D
Transect :
γ (1) =
1
2 × 9
(02
+ 22
+ 02
+ 12
+ 32
+ 42
+ 22
+ 42
+ 02
) = 2.78
γ (2) =
1
2 × 8
(22
+ 22
+ 12
+ 22
+ 12
+ 62
+ 62
+ 42
) = 6.38

20. Example 2D
The directional variograms overlay: the variogram is isotropic.

21. Variogram: anisotropy
Computing the variogram for two pairs of directions.
The anisotropy becomes apparent when computing the pair of
directions 45 and 135 degrees.

22. Variogram map: SST
Skagerrak, 30 June 2005, 2am
The variogram exhibits a more complex anisotropy:
different shapes according to direction.
.

23. Structure analysis
Variogram model
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 18 / 32

24. Variogram calculation and fitting
1) Sample map Variogram Cloud
(small datasets)
2) Experimental variogram 3) Theoretical variogram

25. Nugget-effect variogram
The nugget-effect is equivalent to white noise
0 2 4 6 8 10
0.00.20.40.60.81.0
DISTANCE
VARIOGRAM
q
No spatial structure Discontinuity at the origin

26. Three bounded variogram models
The smoothness of the (simulated) surfaces is linked to
the shape at the origin of γ(h)
Rough Smooth Rough
Spherical model Cubic model Exponential model
0 2 4 6 8 10
0.00.20.40.60.81.0
DISTANCE
VARIOGRAM
0 2 4 6 8 10
0.00.20.40.60.81.0
DISTANCE
VARIOGRAM
0 2 4 6 8 10
0.00.20.40.60.81.0
DISTANCE
VARIOGRAM
Linear at origin Parabolic Linear

27. Power model family
Unbounded variogram variogram models
γ(h) = |h|p
, 0 < p ≤ 2
−10 −5 0 5 10
01234
DISTANCE
VARIOGRAM
p=1.5
p=1
p=0.5
Observe the different behavior at the origin!

28. Nested variogram
Nested variogram
and corresponding random function model
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 23 / 32

29. Nested Variogram Model
Variogram functions can be added to form a nested variogram
Example
A nugget-effect and two spherical structures:
γ(h) = b0 nug(h) + b1 sph(h, a1) + b2 sph(h, a2)
where:
• b0, b1, b2 represent the variances at different scales,
• a1, a2 are the parameters for short and long range.
0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
0.0
0.5
1.0
nugget
longrange
shortrange
(h)γ
h

30. Nested scales
We can define a random function model that goes with the
nested variogram:
Z(x) = Y0(x)
micro-scale
+ Y1(x)
small scale
+ Y2(x)
large scale
This statistical model can be used to extract a specific
component Y(x) from the data.

31. Filtering
Case study: human fertility in France
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 26 / 32

32. Fertility in France
Mean annual number of births per 1000 women over the ’90ies
Nb of women per "commune"
Meanannualfertility’90
0
50
100
150
100 500 5000 10000 25000 50000 5e+05
FERT500 class
FERT500: index for communes with 100 to 500 women.

33. Scales identified on the variogram
Three functions are fitted: nugget-effect, short- and long-range sphericals
Directional
variograms
show isotropy.
D1M1
0. 100. 200. 300. 400.
Distance (km)
0.
10.
20.
30.
40.
50.
60.
70.
80.
90.
100.
110.
Variogram:FERT500
long rangeshort range
The variogram characterizes three scales:
micro-, small- and large-scale variation.

34. Filtering large-scale component
Micro- and small-scale components are removed
Fertility tends to be particularly high in the eastern Bretagne
and above average in the Auvergne.

35. Conclusion
Summary
We have seen that:
the variogram model characterizes the variability at
different scales,
a random function model with several components can be
associated to the structures identified on the variogram,
these components can be extracted by kriging and
mapped.
We will see next how to formulate different kriging algorithms.
Hans Wackernagel (MINES ParisTech) Basics in Geostatistics 1 NERSC • April 2013 30 / 32

36. References
JP Chilès and P Delfiner.
Geostatistics: Modeling Spatial Uncertainty.
Wiley, New York, 2nd edition, 2012.
P. Diggle, M. Fuentes, A.E. Gelfand, and P. Guttorp, editors.
Handbook of Spatial Statistics.
Chapman Hall, 2010.
C Lantuéjoul.
Geostatistical Simulation: Models and Algorithms.
Springer-Verlag, Berlin, 2002.
H Wackernagel.
Multivariate Geostatistics: an Introduction with
Applications.
Springer-Verlag, Berlin, 3rd edition, 2003.

37. Software
Public domain
The free (though not open source) geostatistical software
package RgeoS is available for use in R at:
http://rgeos.free.fr
R is free and available at http://www.r-project.org/
R can be used in a matlab-like graphical environement by
installing additionnally: http://www.rstudio.com/ide/
Commercial
The window and menu driven software Isatis is available
from: http://www.geovariances.com