ฺBasic vector algebra in 2 dimension and 3 dimension
- 2. พีชคณิตของเวกเตอร์ พีชคณิตของเวกเตอร์ (vector algebra) เป็นบทเรียนที่มีเนื้อหาครบคลุมเกี่ยวกับพีชคณิต ของเวกเตอร์ในระบบสองมิติและสามมิติ ในช่วงต้นจะกล่าวถึงพีชคณิตของเวกเตอร์ (vector algebra) คือ การบวก/ลบและการคูณระหว่างเวกเตอร์ (มงคล เดชนครินทร์, 2558, หน้า 425) ใน ส่วนต่อไปจะได้กล่าวถึงผลคูณจุดและผลคูณไขว้ ซึ่งจะเน้นการประยุกต์ใช้กับปัญหาทางฟิสิกส์ กลศาสตร์ บทเรียนเรื่องเวกเตอร์เป็นบทเรียนสำคัญ ช่วยให้ผู้เรียนเกิดทักษะการคำนวณพื้นฐานทาง วิศวกรรมที่สำคัญและจำเป็น เช่น ระบบพิกัดฉาก (rectangular coordinate system) ตรีโกณมิติ ระบบวัดมุม เรขาคณิตวิเคราะห์ ซึ่งจำเป็นต่อการศึกษาทางด้านวิศวกรรมศาสตร์ทั้งสิ้น เหล่านี้ล้วน สอดแทรกอยู่ในเนื้อหาบทเรียนแล้ว ความเข้าใจเกี่ยวกับพีชคณิตของเวกเตอร์ในสามมิติส่งผลให้ ข้อมูลที่ลึกซึ้งมากขึ้น ประยุกต์ใช้งานได้กว้างขวางขึ้น เป็นประตูสู่การแก้ปัญหาที่ซับซ้อนในสาขา ทางด้านวิทยาศาสตร์และวิศวกรรมที่หลากหลายต่อไป พีชคณิตของเวกเตอร์ในสองมิติ 1. เวกเตอร์และสเกลาร์ ปริมาณทางวิทยาศาสตร์ (quantity) ได้จำแนกแบ่งออกเป็น 2 ชนิด คือ 1.1 สเกลาร์ (scalar) เป็นปริมาณที่แสดงออกมาเพียงเฉพาะขนาด (magnitude) เช่น ความยาว ระยะทาง (length) พื้นที่ (area) ปริมาตร (volume) อุณหภูมิ (temperature) และ สัดส่วนความดันโลหิตของร่างกาย (blood pressure) เป็นต้น สำหรับเอกสารประกอบการสอนเล่มนี้ จะใช้อักษรภาษาอังกฤษตัวพิมพ์ใหญ่แบบตัวเอียงเป็นสเกลาร์ เช่น สเกลาร์ 𝐴 1.2 เวกเตอร์ (vector) เป็นปริมาณที่แสดงออกมาทั้งขนาดและทิศทาง (magnitude and direction) นิยมใช้กับการศึกษาด้านวิทยาศาสตร์ เทคโนโลยี และวิศวกรรม โดยเฉพาะในวิชา ฟิสิกส์ คณิตศาสตร์ กลศาสตร์วิศวกรรม พบมากในรูปแบบของปริมาณ เช่น ความเร็ว (velocity) ความเร่ง (acceleration) แรง (force) โมเมนต์ (moment) เป็นต้น สำหรับเอกสารประกอบการสอน เล่มนี้จะใช้อักษรภาษาอังกฤษตัวพิมพ์ใหญ่แบบตัวตรงกำกับด้วยเครื่องหมายลูกศรเหนืออักษร เช่น เวกเตอร์ A ⃗ ⃗ ต้องการเพียงขนาด อธิบายขนาดของเวกเตอร์ได้เป็น |A ⃗ ⃗ |
- 3. 2 ส่วนของเส้นตรงที่ลากจากจุดกำเนิด 𝑂(0,0) ไปยังจุด 𝑃(𝑥1, 𝑦1) โดยใช้ลูกศรแสดง ทิศทางของเวกเตอร์โดยให้หางของลูกศรอยู่ที่จุด 𝑂 และหัวลูกศรอยู่ที่จุด 𝑃 เราสามารถนำเสนอ เวกเตอร์โดยมีชื่อเรียกตามลำดับจากจุดกำเนิด 𝑂 ไปยังจุด 𝑃 ได้เป็นเวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ ดังภาพที่ 1.1 ภาพที่ 1.1 เวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ ที่ลากจากจุดกำเนิด 𝑂(0,0) ไปยังจุด 𝑃(𝑥1, 𝑦1) 2. การเท่ากันของเวกเตอร์ เวกเตอร์ 2 เวกเตอร์ใดๆ จะเท่ากันก็ต่อเมื่อมีขนาดเท่ากันและมีทิศทางเดียวกัน (ศรีบุตร แววเจริญ และ ชนศักดิ์ บ่ายเที่ยง, 2542, หน้า 112) ดังภาพที่ 1.2 ภาพที่ 1.2 การเท่ากันของเวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ = 𝑄𝑅 ⃗⃗⃗⃗⃗ จากภาพที่ 1.2 พบว่าขนาดและทิศทางของเวกเตอร์ทั้งสอง มีค่าเท่ากันทั้งคู่ และเวกเตอร์ขนานกัน (parallel vector) แม้ว่าทั้งคู่อยู่ต่างจุดพิกัดซึ่งเป็นการเท่ากันของเวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ = 𝑄𝑅 ⃗⃗⃗⃗⃗ เช่น กำหนดให้ขนาดของเวกเตอร์ |𝑂𝑃 ⃗⃗⃗⃗⃗ | = 5 และ |𝑄𝑅 ⃗⃗⃗⃗⃗ | = 5 ถ้าทิศทางของทั้งสองเวกเตอร์มีค่า เท่ากัน ดังนั้นสรุปได้ว่าเวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ = 𝑄𝑅 ⃗⃗⃗⃗⃗ ทุกประการ 𝑂(0,0) 𝑃(𝑥1, 𝑦1) 𝑂𝑃 ⃗⃗⃗⃗⃗ 𝑂(0,0) 𝑃(𝑥1, 𝑦1) 𝑂𝑃 ⃗⃗⃗⃗⃗ 𝑄(𝑥1, 𝑦1) 𝑅(𝑥2, 𝑦2) 𝑄𝑅 ⃗⃗⃗⃗⃗
- 4. 3 3. การบวกเวกเตอร์ การบวกกันของเวกเตอร์ 2 เวกเตอร์ใด ๆ ทำได้โดยเขียนเส้นตรงบอกทิศทางที่แทนด้วย เวกเตอร์ทั้งสอง โดยให้จุดเริ่มต้นของเวกเตอร์ที่นำมาบวกอยู่ที่จุดปลายของเวกเตอร์ที่เป็นตัวตั้ง แล้ว ลากจากจุดเริ่มต้นของเวกเตอร์ ที่เป็นตัวตั้งไปยังจุดปลายของเวกเตอร์อีกเวกเตอร์หนึ่ง เวกเตอร์ที่ เกิดขึ้นใหม่คือ ผลบวกของเวกเตอร์ทั้งสอง เช่น เวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ + 𝐶𝐷 ⃗⃗⃗⃗⃗ = 𝐴𝐷 ⃗⃗⃗⃗⃗ ดังรูปที่ 1.3 ภาพที่ 1.3 ผลบวกของเวกเตอร์ทั้งสอง หรือ เวกเตอร์ลัพธ์ การบวกเวกเตอร์ที่แสดงดังภาพที่ 1.3 เป็นวิธีหาผลบวกเวกเตอร์ขั้นพื้นฐาน ซึ่งสามารถนำเสนอใน รูปแบบอื่นตามความเหมาะสม ด้วยกฎสี่เหลี่ยมด้านขนาน (parallelogram law) (Zill, 2018, pp.322) ดังภาพที่ 1.4 ภาพที่ 1.4 ผลบวกเวกเตอร์ด้วยกฎสี่เหลี่ยมด้านขนาน 𝐴 𝐵 𝐴𝐵 ⃗⃗⃗⃗⃗ 𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐶 𝐷 𝐴𝐷 ⃗⃗⃗⃗⃗ 𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐴 𝐵 𝐴𝐵 ⃗⃗⃗⃗⃗ 𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐶 𝐷 𝐴𝐷 ⃗⃗⃗⃗⃗ 𝐴𝐵 ⃗⃗⃗⃗⃗
- 5. 4 4. การลบเวกเตอร์ นิเสธของเวกเตอร์ 𝐶𝐷 ⃗⃗⃗⃗⃗ คือเวกเตอร์ที่มีขนาดเท่ากับเวกเตอร์ 𝐶𝐷 ⃗⃗⃗⃗⃗ แต่มีทิศทางตรง ข้าม นิเสธของเวกเตอร์ 𝐶𝐷 ⃗⃗⃗⃗⃗ เขียนแทนด้วยสัญลักษณ์ −𝐶𝐷 ⃗⃗⃗⃗⃗ ดังภาพที่ 1.5 ภาพที่ 1.5 นิเสธของเวกเตอร์ 𝐶𝐷 ⃗⃗⃗⃗⃗ การลบกันของเวกเตอร์ 2 เวกเตอร์ใด ๆ ทำได้โดยเช่นเดียวกับ การบวกเวกเตอร์ แต่จะต้อง ดำเนินการขยายความนิเสธของเวกเตอร์ที่จะลบเสียก่อน เช่น เวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ − 𝐶𝐷 ⃗⃗⃗⃗⃗ มีความหมาย เท่ากับ เวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ + (−𝐶𝐷 ⃗⃗⃗⃗⃗ ) จากนั้นดำเนินการเช่นเดียวกับการบวกเวกเตอร์ ดังภาพ 1.6 ภาพที่ 1.6 ความหมายของการลบเวกเตอร์ 𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐶 𝐷 −𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐷 𝐶 𝐴 𝐵 𝐴𝐵 ⃗⃗⃗⃗⃗ −𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐶 𝐷 𝐴𝐵 ⃗⃗⃗⃗⃗ + (−𝐶𝐷 ⃗⃗⃗⃗⃗ ) 𝐴 𝐵 𝐴𝐵 ⃗⃗⃗⃗⃗ 𝐶 𝐷 𝐶𝐷 ⃗⃗⃗⃗⃗ 𝐷𝐵 ⃗⃗⃗⃗⃗⃗
- 6. 5 5. การคูณเวกเตอร์ด้วยสเกลาร์ การคูณเวกเตอร์ด้วยสเกลาร์หรือผลคูณเวกเตอร์เชิงสเกลาร์ (scalar multiple) โดย กำหนดให้เวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ และปริมาณสเกลาร์ k ดำเนินการคูณกันในลักษณะ 𝑘𝐴𝐵 ⃗⃗⃗⃗⃗ ซึ่งการ ดำเนินการในลักษณะดังกล่าวเป็นการคูณเวกเตอร์ด้วยสเกลาร์ การคูณเวกเตอร์ด้วยสเกลาร์ เปรียบเสมือนเป็นการปรับขนาดเวกเตอร์ให้มีความยาวเพิ่มขึ้นหรือสั้นลงได้อีกด้วย โดยตัวเลขที่อยู่ใน ปริมาณสเกลาร์ k จะต้องมีปริมาณขนาดอยู่เท่านั้น หรือ |𝑘| > 0 จึงส่งผลต่อการปรับเพิ่มลด ขนาดของเวกเตอร์ได้ ดังภาพที่ 1.7 ภาพที่ 1.7 การปรับเพิ่มลดขนาดของเวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ ด้วยการคูณเวกเตอร์ด้วยสเกลาร์ จากภาพที่ 1.7 เวกเตอร์ 𝐴𝐵 ⃗⃗⃗⃗⃗ ทางด้านซ้ายมือสุด ถูกดำเนินการด้วยการคูณเวกเตอร์ด้วยสเกลาร์ใน ลักษณะ 𝑘𝐴𝐵 ⃗⃗⃗⃗⃗ ผลลัพธ์ที่ได้มีความแตกต่างออกไปจากเดิม เช่น เมื่อ 𝑘 = −1 ส่งผลให้ทิศทาง ของเวกเตอร์จากเดิมปรับเปลี่ยนเป็นด้านตรงข้ามกัน (เช่นเดียวกับการลบเวกเตอร์) 𝑘 = 3 2 ส่งผล ให้เวกเตอร์มีทิศทางเดิมแต่ขนาดมีการขยายยืดความยาวออกไป 3 2 เท่าของเวกเตอร์เดิม เป็นต้น สำหรับกรณีนี้อาจเรียกเป็นการหารเวกเตอร์ด้วยสเกลาร์ก็ได้ 6. เวกเตอร์ในเชิงเรขาคณิต ในเรขาคณิตวิเคราะห์ได้มีการประยุกต์ใช้เวกเตอร์อย่างแพร่หลาย โดยเฉพาะอย่างยิ่งใน การแสดงพิกัดของตำแหน่งบนระนาบ (plane) หรือในปริภูมิสามมิติ (space) หมายถึงเวกเตอร์ใน ปริภูมิ 𝑅2 และ 𝑅3 นั้นจะแสดงขนาดและทิศทางเทียบเท่ากับปริมาณในจุดกำเนิด (origin) ถึงจุด พิกัด (coordinate) หนึ่ง (นิติการ นิ่มสุข, 2561, หน้า 8) เวกเตอร์บนระนาบ 𝑅2 หมายถึงเวกเตอร์ ในระนาบสองมิติ ในด้านความหมายและการดำเนินการต่างๆ บนเวกเตอร์ในเชิงเรขาคณิต สามารถ
- 7. 6 𝑂𝑃 ⃗⃗⃗⃗⃗ 𝑥 𝑦 𝑂(0,0) 𝑃(𝑥1, 𝑦1) 𝑥1 𝑦1 อธิบายลักษณะของเวกเตอร์ โดยกำหนดให้เวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ ∈ 𝑅2 (เวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ อยู่ในระนาบสอง มิติ) เป็นเวกเตอร์ตำแหน่ง (position vector) เช่น เวกเตอร์ตำแหน่ง 𝑂𝑃 ⃗⃗⃗⃗⃗ ดังภาพที่ 1.8 ภาพที่ 1.8 เวกเตอร์ตำแหน่ง จากภาพที่ 1.8 ได้แสดงรายละเอียดอธิบายลักษณะของเวกเตอร์และมีความสัมพันธ์ ดังสมการที่ 1.1 𝑂𝑃 ⃗⃗⃗⃗⃗ = [ 𝑥1 𝑦1 ] (1.1) โดยกำหนดให้ชื่อเวกเตอร์ 𝑂𝑃 ⃗⃗⃗⃗⃗ อยู่ทางซ้ายมือของสมการและทางขวามือแสดงระยะห่างของแกน นอนและแกนยืนในลักษณะคล้ายกับคู่อันดับโดยสมาชิกภายในของเวกเตอร์จัดเรียงจากบนลงล่าง สามารถนำเสนอเวกเตอร์ตำแหน่ง 𝑂𝑃 ⃗⃗⃗⃗⃗ ในอีกรูปแบบหนึ่งที่สะดวกต่อการดำเนินการทางพีชคณิต แสดงดังสมการที่ 1.2 (Zill, 2018, pp.323) 𝑂𝑃 ⃗⃗⃗⃗⃗ = 〈𝑥1, 𝑦1〉 (1.2) 7. องค์ประกอบเวกเตอร์ องค์ประกอบเวกเตอร์ (component vector) กำหนดให้เวกเตอร์ a เป็นเวกเตอร์ที่อยู่ ในระนาบสองมิติ 𝐚 ∈ 𝑅2 โดยที่เวกเตอร์ a มีองค์ประกอบเป็น 𝑎1, 𝑎2 ดังภาพที่ 1.9
- 8. 7 𝒂 𝑥 𝑦 𝑃(𝑎1, 𝑎2) 𝑎1 𝑎2 ภาพที่ 1.9 องค์ประกอบเวกเตอร์ จากภาพที่ 1.9 ได้อธิบายองค์ประกอบเวกเตอร์และมีความสัมพันธ์ ดังสมการที่ 1.3 𝐚 = 〈𝑎1, 𝑎2〉 (1.3) กำหนดให้จุดเริ่มต้นอยู่ที่ 𝑃1(𝑥, 𝑦) จุดปลายที่ 𝑃2(𝑥 + 4, 𝑦 + 3) ดังภาพที่ 1.10 จะได้ เวกเตอร์ตำแหน่ง 𝐚 = 〈4,3〉 เทียบเท่ากับระยะขจัดซึ่งยังคงรักษาองค์ประกอบไว้ครบถ้วน ภาพที่ 1.10 การเปลี่ยนแปลงจุดเริ่มต้น 𝑃1(𝑥, 𝑦) และเวกเตอร์ตำแหน่ง
- 9. 8 จากหัวข้อการบวกเวกเตอร์ การลบเวกเตอร์ การคูณเวกเตอร์ด้วยสเกลาร์ สามารถอธิบาย เป็นนิยามโดยสรุปในตารางที่ 1.1 ตารางที่ 1.1 นิยามการ การคูณเวกเตอร์ด้วยสเกลาร์ และการเท่ากัน นิยามที่ 1.1 การบวก การคูณเชิงสเกลาร์ และการเท่ากัน กำหนดให้ 𝐚 = 〈𝑎1, 𝑎2〉 และ 𝐛 = 〈𝑏1, 𝑏2〉 เป็นเวกเตอร์ใน 𝑅2 ลำดับที่ ชื่อนิยาม คำอธิบาย 1 การบวก 𝐚 + 𝐛 = 〈𝑎1 + 𝑏1, 𝑎2 + 𝑏2〉 2 การคูณเชิงสเกลาร์ 𝑘𝑎 = 〈𝑘𝑎1, 𝑘𝑎2〉 3 การเท่ากัน 𝐚 = 𝐛 โดยที่ 𝑎1 = 𝑏1และ 𝑎2 = 𝑏2 ตัวอย่างที่ 1.1 กำหนดให้เวกเตอร์ 𝐚 = 〈1,4〉 และ 𝐛 = 〈−6,3〉 จงหา 𝐚 + 𝐛 วิธีทำ เราสามารถหาผลการบวกเวกเตอร์โดยใช้นิยามที่ 1 ข้อ 1 ได้เป็น 𝐚 + 𝐛 = 〈1 + 4, −6 + 3〉 = 〈5, −3〉 ∴ 𝐚 + 𝐛 = 〈5, −3〉 ตอบ ตัวอย่างที่ 1.2 กำหนดให้เวกเตอร์ 𝐚 = 〈1,4〉 และ 𝐛 = 〈−6,3〉 จงหา 𝐚 − 𝐛 วิธีทำ เราสามารถหาผลการบวกเวกเตอร์โดยใช้นิยามที่ 1 ข้อ 2 ได้เป็น 𝐚 − 𝐛 = 〈1 − 4, −6 − 3〉 = 〈−3, −9〉 ∴ 𝐚 + 𝐛 = 〈−3, −9〉 ตอบ
- 10. 9 ตัวอย่างที่ 1.3 กำหนดให้เวกเตอร์ 𝐚 = 〈1,4〉 และ 𝐛 = 〈−6,3〉 จงหา 2𝐚 + 𝟑𝐛 วิธีทำ เราสามารถหาผลการบวกเวกเตอร์โดยใช้ นิยามที่ 1 ข้อ 1 และ 2 ได้เป็น 𝟐𝐚 + 𝟑𝐛 = 〈2(1), 2(4)〉 + 〈3(−6), 3(3)〉 = 〈2,8〉 + 〈−18,9〉 = 〈2 + (−18), 8 + 9〉 = 〈2 − 18,8 + 9〉 = 〈−16,17〉 ∴ 𝟐𝐚 + 𝟑𝐛 = 〈−16,17〉 ตอบ 8. คุณสมบัติ นิยามที่ได้แสดงในตารางข้างต้น สามารถนำมาสรุปเป็นคุณสมบัติซึ่งเรียกว่าคุณสมบัติ ทางพีชคณิตของเวกเตอร์ในระนาบสองมิติ 𝑅2 โดยสรุปเป็นทฤษฎีบทในตารางที่ 1.2 ตารางที่ 1.2 คุณสมบัติทางพีชคณิตของเวกเตอร์ในระนาบสองมิติ 𝑅2 ทฤษฎีบทที่ 1.1 คุณสมบัติของเวกเตอร์ ลำดับที่ คุณสมบัติ ชื่อเรียก 1 𝐚 + 𝐛 = 𝐛 + 𝐚 กฎการสลับที่ 2 𝐚 + (𝐛 + 𝐜) = (𝐚 + 𝐛) + 𝐜 กฎการเปลี่ยนหมู่ 3 𝐚 + 𝟎 = 𝐚 เอกลักษณ์การเพิ่มเติม 4 𝐚 + (−𝐚) = 𝟎 การเพิ่มเติมเพื่อหักล้าง 5 𝑘(𝐚 + 𝐛) = 𝑘𝐚 + 𝑘𝐛 6 (𝑘1 + 𝑘2)𝐚 = 𝑘1𝐚 + 𝑘2𝐚 7 𝑘1(𝑘2𝐚) = (𝑘1𝑘2𝐚) 8 𝟏𝐚 = 𝐚 9 𝟎𝐚 = 𝟎 เวกเตอร์ศูนย์ โดยที่ 𝑘 ในตารางที่ 1.2 ข้อ 5-7 เป็นสเกลาร์ และ เวกเตอร์ศูนย์ (zero vector) ข้อ 3, 4 และ 9 กำหนดให้มีนิยามของเวกเตอร์ศูนย์มีองค์ประกอบของเวกเตอร์เป็น 𝟎 = 〈0,0〉
- 11. 10 9. ขนาดเวกเตอร์ ความหมายของขนาดเวกเตอร์ (magnitude) มีความหมายเช่นเดียวกันกับ ระยะทาง (length) และ นอร์ม (norm) ดังนั้นขนาดของเวกเตอร์ 𝐚 กำหนดให้ใช้สัญกรณ์เป็น ‖𝐚‖ โดยใช้ หลักการด้านสามเหลี่ยมมุมฉากของทฤษฎีบทพีทาโกรัส (Pythagorean theorem) ดังภาพที่ 1.11 ภาพที่ 1.11 ขนาดของเวกเตอร์ 𝐚 และด้านสามเหลี่ยมมุมฉากของทฤษฎีพีทาโกรัส จากภาพที่ 1.11 องค์ประกอบของเวกเตอร์ 𝐚 มีค่าเป็น 𝐚 = 〈𝑎1, 𝑎2〉 กำหนดให้การหาขนาด ของเวกเตอร์ 𝐚 นิยามได้เป็นสมการที่ 1.4 (Zill, 2018, pp.324) ‖𝐚‖ = √𝑎1 2 + 𝑎2 2 (1.4) ความหมายขนาดของเวกเตอร์ จะต้องมีปริมาณอยู่เสมอ ดังนั้น ‖𝐚‖ ≥ 0 ถ้าเวกเตอร์มีปริมาณ เป็นศูนย์ ‖𝐚‖ = 0 จะถูกทำให้เวกเตอร์ดังกล่าวเป็นเวกเตอร์ศูนย์ 𝐚 = 𝟎 ตัวอย่างที่ 1.4 จงหาขนาดเวกเตอร์ เมื่อกำหนดให้เวกเตอร์ 𝐚 = 〈6, −2〉 วิธีทำ เราสามารถหาขนาดของเวกเตอร์โดยใช้สมการที่ 1.4 ‖𝐚‖ = √62 + (−2)2 = √36 + 4 = √22 × 10 = √22√10 ∴ ‖𝐚‖ = 2√10 ตอบ
- 12. 11 10. เวกเตอร์หนึ่งหน่วย เวกเตอร์ขนาดหนึ่งหน่วย (unit vector) เป็นการจัดเรียงความยาวของขนาดเวกเตอร์ จากหน่วยเต็มให้มีความเป็นมาตรฐานเดียวกัน (normalization) เช่น ระยะความยาวของไม้บรรทัดที่ มีความยาวทั้งสิ้น 30 เซนติเมตร หรือ 12 นิ้ว ความแตกต่างกันระหว่างหน่วย เซนติเมตร และนิ้ว จะต้องถูกเรียงใหม่ให้มีความเป็นมาตรฐานเดียวกันในระบบใดระบบหนึ่งนั่นเอง สำหรับเวกเตอร์ที่มี ขนาดหนึ่งหน่วยและชี้ไปในทิศทางเดียวกันกับเวกเตอร์ที่มีความยาวหน่วยเต็ม เราจะเรียกว่าเวกเตอร์ หนึ่งหน่วยของเวกเตอร์นั้นๆ เช่น เวกเตอร์ 𝐚 มีขนาดความยาวของเวกเตอร์ทั้งสิ้น 5 หน่วย ดังนั้น ‖𝐚‖ = 5 ในขณะเดียวกันก็จะมีเวกเตอร์อีกอันหนึ่งซึ่งมีทิศทางเดียวกับเวกเตอร์ 𝐚 ซึ่งมีความ ยาวเท่ากับ 1 หน่วย อยู่ร่วมกันอยู่บนเวกเตอร์ 𝐚 นั่นคือเวกเตอร์หนึ่งหน่วย 𝐮 ซึ่งลักษณะของการ คำนวณหาเวกเตอร์หนึ่งหน่วยอาจเรียกว่าการทำให้มีความเป็นมาตรฐานเดียวกัน ดังสมการที่ 1.5 𝐮 = 𝐚 ‖𝐚‖ (1.5) ตัวอย่างที่ 1.5 จงหาเวกเตอร์หนึ่งหน่วย เมื่อกำหนดให้เวกเตอร์ 𝐚 = 〈2, −1〉 วิธีทำ เราสามารถหาเวกเตอร์หนึ่งหน่วยโดยใช้สมการที่ 1.5 1. หาขนาดเวกเตอร์ 𝐚 ‖𝐚‖ = √22 + (−1)2 = √4 + 1 ∴ ‖𝐚‖ = √5 2. แทนค่าลงในสมการ 1.5 𝐮 = 𝐚 ‖𝐚‖ = 〈2, −1〉 √5 = 1 √5 〈2, −1〉 ∴ 𝐮 = 〈 2 √5 , − 1 √5 〉 ตอบ
- 13. 12 11. เวกเตอร์ 𝐢 และ 𝐣 เวกเตอร์ใน 2 มิติ 𝑅2 ในแต่ละแกนจะมีเวกเตอร์หนึ่งหน่วยคูณเชิงสเกลาร์กับแกนอยู่ โดยที่เวกเตอร์ขนาดหนึ่งหน่วยที่คูณเชิงสเกลาร์กับแกน 𝑥 จะใช้ชื่อว่าเวกเตอร์ 𝐢 และเวกเตอร์ขนาด หนึ่งหน่วยที่คูณเชิงสเกลาร์กับแกน 𝑦 จะใช้ชื่อว่าเวกเตอร์ 𝐣 ตามลำดับ แสดงดังภาพที่ 1.12 ภาพที่ 1.12 เวกเตอร์ 𝐢 และ 𝐣 ความสัมพันธ์จากภาพที่ 1.12 เราสามารถอธิบายความสัมพันธ์เป็นผลบวกระหว่างเวกเตอร์ 𝐚 โดยที่ 𝐚 = 〈𝑎1, 𝑎2〉 กับเวกเตอร์ 𝐢 และ 𝐣 ได้เป็น สมการที่ 1.6 และ 1.7 〈𝑎1, 𝑎2〉 = 〈𝑎1, 0〉 + 〈0, 𝑎2〉 (1.6) 〈𝑎1, 𝑎2〉 = 𝑎1〈1,0〉 + 𝑎2〈0,1〉 (1.7) โดยกำหนดให้เวกเตอร์ 〈1,0〉 และเวกเตอร์ 〈0,1〉 เป็นเวกเตอร์ขนาดหนึ่งหน่วยซึ่งดำเนินไปใน ทิศทางตามแนวแกนนอนและแกนยืนตามลำดับ ดังนั้นสามารถสรุปได้ดังสมการที่ 1.8, 1.9 และ 1.10 𝐢 = 〈1,0〉 (1.8) 𝐣 = 〈0,1〉 (1.9) 〈𝑎1, 𝑎2〉 = 𝑎1𝐢 + 𝑎2𝐣 (1.10)
- 14. 13 ตัวอย่างที่ 1.6 จงดำเนินการทางพีชคณิตในรูปแบบของเวกเตอร์ 𝐢 และ 𝐣 ก) 〈4,7〉 = 4𝐢 + 7𝐣 ข) (2𝐢 − 5𝐣) + (8𝐢 + 13𝐣) = 10𝐢 + 8𝐣 ค) ‖𝐢 + 𝐣‖ = √2 ง) 10(3𝐢 − 𝐣) = 30𝐢 − 10𝐣 จ) 𝐚 = 6𝐢 + 4𝐣 และ 𝐛 = 9𝐢 + 6𝐣 โดยสองเวกเตอร์นี้ขนานกัน เมื่อพิจารณาในเรื่องของการคูณสเกลาร์ของเวกเตอร์ 𝐛 เทียบกับเวกเตอร์ 𝐚 สรุปได้เป็น 𝐛 = 3 2 (6𝐢 + 4𝐣) หรือ 𝐛 = 3 2 𝐚 ตัวอย่างที่ 1.7 กำหนดให้เวกเตอร์ 𝐚 = 4𝐢 + 2𝐣 และ 𝐛 = −2𝐢 + 5𝐣 จงคำนวณหา 𝐚 + 𝐛 และ 𝐚 − 𝐛 โดยแสดงเวกเตอร์ลัพธ์เป็นแผนภาพเวกเตอร์ วิธีทำ 𝐚 + 𝐛 = 2𝐢 + 7𝐣 และ 𝐚 − 𝐛 = 6𝐢 − 3𝐣 แสดงเวกเตอร์ลัพธ์เป็นแผนภาพเวกเตอร์ได้ดังภาพที่ 1.13 ภาพที่ 1.13 แสดงเวกเตอร์ลัพธ์เป็นแผนภาพเวกเตอร์ ตอบ
- 15. 14 พีชคณิตของเวกเตอร์ในสามมิติ การอธิบายความสัมพันธ์ของจุดใดๆ ในสองมิติ เช่น กำหนดให้จุด 𝑃 เป็นจุดที่อยู่ในสองมิติ ดังนั้นจุด 𝑃 จะต้องมีพิกัดอันเกิดจากเส้นตัดผ่านแกน 𝑥 โดยตั้งฉากกันและเส้นตัดผ่านแกน 𝑦 แบบ ตั้งฉากกัน โดยกำหนดให้เส้นตรงที่ตัดผ่านแกน 𝑥 มีค่า 𝑥 = 𝑎 และเส้นตรงที่ตัดผ่านแกน 𝑦 มีค่า เป็น 𝑦 = 𝑏 เป็นคู่อันดับ (𝑎, 𝑏) ที่จุด 𝑃 เป็นระบบพิกัดฉากสองมิติ 𝑃(𝑎, 𝑏) ดังภาพที่ 1.14 โดยระบบพิกัดฉากสองมิติอาจเรียกว่า “ระนาบ 𝑥𝑦” ภาพที่ 1.14 ระบบพิกัดฉากสองมิติ 1. ระบบพิกัดฉากสามมิติ ระบบพิกัดฉากสามมิติประกอบด้วยแกน 3 แกน ทั้งสามแกนตั้งฉากซึ่งกันและกัน จุดที่ แกนทั้งสามตัดกันเรียกว่าจุดกำเนิด (origin) ใช้อักษรโอใหญ่ “𝑂” ทั้งสามแกนมีชื่อแกนเรียงลำดับ ตามกฎมือขวาเรียงตามลำดับ 𝑥, 𝑦, 𝑧 โดยใช้นิ้วมือขวาเยียดตรง นิ้วมือเหล่านั้นจะชี้ไปในทิศทาง ของแกน 𝑥 เมื่อพับนิ้วมือดังกล่าวโค้งงอเข้าหาข้อมือ จะเป็นลำดับของทิศทางแกน 𝑦 จากนั้นยก นิ้วหัวแม่มือขึ้น จะชี้ไปในทิศทางของแกนใหม่ที่ตั้งฉากกับระนาบของแกน 𝑥 และ 𝑦 แกนใหม่นี้มีชื่อ ว่าแกน 𝑧 โดยเส้นประที่ปรากฏ แสดงถึงด้านลบของในแต่ละแกน ดังภาพที่ 1.15
- 16. 15 ภาพที่ 1.15 แกน 𝑥, 𝑦, 𝑧 ตามกฎมือขวา ที่มา (Zill, 2018, pp.328) กำหนดให้ระนาบที่ตั้งฉากกับแกน 𝑥 แกน 𝑦 และแกน 𝑧 ตามลำดับ จุด 𝑃 ที่ระนาบเหล่านี้ตัดกัน สามารถแสดงด้วยตัวเลขสามตัวลำดับ (𝑎, 𝑏, 𝑐) ซึ่งบ่งบอกได้ว่าเป็นพิกัดสี่เหลี่ยมหรือพิกัดฉาก ของจุดเป็นระบบพิกัดฉากสามมิติ 𝑃(𝑎, 𝑏, 𝑐) ดังภาพที่ 1.16 ภาพที่ 1.16 ระบบพิกัดฉากสามมิติ 𝑃(𝑎, 𝑏, 𝑐) ที่มา (Zill, 2018, pp.328)
- 17. 16 2. อัฐภาค ระนาบคือแผ่นที่เกิดจากพิกัดฉากของแกนสองแกนประกอบกัน จึงเรียกสิ่งนี้ว่าระนาบ เช่น ระนาบ 𝑥𝑦 เกิดพิกัดแกน 𝑥 และ 𝑦 ประกอบกัน สำหรับพิกัดแกน 𝑥 และ 𝑧 กำหนดให้เป็น ระนาบ 𝑥𝑧 และอื่นๆ ระนาบในพิกัดสามมิติแบ่งออกได้เป็นแปดส่วน ในแต่ละส่วนที่ปรากฎออกมา เรียกว่า อัฐภาค (octant) ดังภาพที่ 1.17 โดยอัฐภาคแรกประกอบด้วยพิกัดแกน 𝑥, 𝑦, 𝑧 มีค่าเป็น บวกทั้งหมด ซึ่งเราสามารถสรุปอัฐภาคในพิกัดแกนต่างๆ ได้ดังตารางที่ 1.3 ภาพที่ 1.17 อัฐภาค ที่มา (Zill, 2018, pp.328) ตารางที่ 1.3 อัฐภาคในพิกัดแกนต่างๆ แกน พิกัด ระนาบ พิกัด 𝑥 (𝑎, 0,0) 𝑥𝑦 (𝑎, 𝑏, 0) 𝑦 (0, 𝑏, 0) 𝑥𝑧 (𝑎, 0, 𝑐) 𝑧 (0,0, 𝑐) 𝑦𝑧 (0, 𝑏, 𝑐)
- 18. 17 3. จุดพิกัดในระบบสามมิติ กำหนดให้พล๊อตจุดพิกัด ได้แก่ (4,5,6), (3, −3, −1) และ (−2, −2,0) ตามลำดับ สามารถแสดงผลการพล๊อตจุดพิกัดต่างๆ ดังภาพที่ 1.18 ภาพที่ 1.18 ผลการพล๊อตจุดพิกัด 4. ระยะห่างระหว่างจุดพิกัดในระบบสามมิติ กำหนดให้จุดในระบบสามมิติจำนวนสองจุด ได้แก่ 𝑃1(𝑥1, 𝑦1, 𝑧1) และ 𝑃2(𝑥2, 𝑦2, 𝑧2) โดยให้พิจารณาภาพฉายบนระนาบ 𝑥𝑦 เสียก่อน ซึ่งจะมีจุด 𝑃1 และ 𝑃2 ให้ พิจารณาบนระนาบ 𝑥𝑦 เป็น (𝑥1, 𝑦1, 0) และ (𝑥2, 𝑦2, 0) ดังภาพที่ 1.19 ภาพที่ 1.19 การหาระยะห่างระหว่างจุดพิกัดในระบบสามมิติพิจารณาภาพฉายบนระนาบ 𝑥𝑦
- 19. 18 เส้นประอ้างอิงบนระนาบ 𝑥𝑦 ในภาพที่ 1.19 เป็นฉายภาพระยะทางระหว่างจุดพิกัด 𝑃1 และ 𝑃2 และสามารถใช้หลักการด้านสามเหลี่ยมมุมฉากของทฤษฎีบทพีทาโกรัส เพื่อคำนวณหาระยะทาง ระหว่างจุดพิกัด 𝑃1 และ 𝑃2 ตามเส้นประอ้างอิงได้เป็น √(𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2 โดยที่พิกัด 𝑃3 เป็นพิกัด (𝑥2, 𝑦2, 𝑧1) ดังนั้นหาระยะห่างได้เป็นดังสมการที่ 1.11 และ 1.12 [𝑑(𝑃1, 𝑃2)]2 = [√(𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2] + |𝑧2 − 𝑧1|2 (1.11) 𝑑(𝑃1, 𝑃2) = √(𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2 + (𝑧2 − 𝑧1)2 (1.12) ตัวอย่างที่ 1.8 จงหาระยะห่างระหว่าง (2, −3,6) และ (−1, −7,4) วิธีทำ กำหนดชื่อจุดพิกัด 𝑃2(2, −3,6) และ 𝑃1(−1, −7,4) และใช้สมการ 1.12 𝑑(𝑃1, 𝑃2) = √(2 − (−1))2 + (−3 − (−7))2 + (6 − 4)2 = √(2 + 1)2 + (−3 + 7)2 + (6 − 4)2 = √(3)2 + (4)2 + (2)2 = √9 + 16 + 4 = √29 ตอบ 5. จุดกึ่งกลางระหว่างจุดพิกัดในระบบสามมิติ การหาจุดกึ่งกลางระหว่างจุดพิกัดในระบบสองมิติมีวิธีดำเนินการในลักษณะคล้ายคลึง กับการหาจุดกึ่งกลางระหว่างจุดพิกัดในระบบสามมิติ โดยกำหนดให้จุดสองจุดในระบบสามมิติเป็น 𝑃1(𝑥1, 𝑦1, 𝑧1) และ 𝑃2(𝑥2, 𝑦2, 𝑧2) เป็นจุดที่แตกต่างกันสองจุด ดังนั้นสามารถ คำนวณหาพิกัดของจุดกึ่งกลางระหว่างจุดพิกัดในระบบสามมิติได้เป็นดังสมการที่ 1.13 ( 𝑥1 + 𝑥2 2 , 𝑦1 + 𝑦2 2 , 𝑧1 + 𝑧2 2 ) (1.13)
- 20. 19 ตัวอย่างที่ 1.9 จงหาจุดกึ่งกลางระหว่างพิกัด (2, −3,6) และ (−1, −7,4) วิธีทำ กำหนดชื่อจุดพิกัด 𝑃2(2, −3,6) และ 𝑃1(−1, −7,4) และใช้สมการ 1.13 ( −1 + 2 2 , −7 + (−3) 2 , 4 + 6 2 ) = ( −1 2 , −10 2 , 10 2 ) = (− 1 2 , −5,5) ตอบ 6. เวกเตอร์ในสามมิติ เวกเตอร์ในสามมิติ (vectors in 3-space) เป็นการนำจำนวนจริงมาเรียบเรียงลำดับกัน สามลำดับสอดคล้องลำดับเป็นไปตามแกน 𝑥, 𝑦, 𝑧 ดังสมการที่ 1.14 𝐚 = 〈𝑎1, 𝑎2, 𝑎3〉 (1.14) โดยที่ 𝑎1, 𝑎2 และ 𝑎3 เป็นองค์ประกอบของเวกเตอร์ โดยใช้อักษรย่อระบบในสามมิติว่า 𝑅3 กำหนดให้จุด 𝑃(𝑥1, 𝑦1, 𝑧1) และจุด 𝑂(0,0,0) เราสามารถหาเวกเตอร์ตำแหน่งได้เป็น 𝑂𝑃 ⃗⃗⃗⃗⃗ = 〈𝑥1, 𝑦1, 𝑧1〉 ดังภาพที่ 1.20 ภาพที่ 1.20 เวกเตอร์ตำแหน่ง 𝑃(𝑥1, 𝑦1, 𝑧1)
- 21. 20 คุณสมบัติทางด้าน การเท่ากันของเวกเตอร์ การบวกเวกเตอร์ การลบเวกเตอร์ การคูณ เวกเตอร์ด้วย สเกลาร์ องค์ประกอบเวกเตอร์ และคุณสมบัติอื่นๆ ขององค์ประกอบเวกเตอร์ในสามมิติ เป็นไปตามนิยามที่ 1.2 โดยสรุปในตารางที่ 1.4 ตารางที่ 1.4 คุณสมบัติ นิยาม องค์ประกอบเวกเตอร์ในสามมิติ นิยามที่ 1.2 องค์ประกอบเวกเตอร์ในสามมิติ กำหนดให้ 𝐚 = 〈𝑎1, 𝑎2, 𝑎3〉 และ 𝐛 = 〈𝑏1, 𝑏2, 𝑏3〉 เป็นเวกเตอร์ในสามมิติ 𝑅3 ลำดับที่ ชื่อนิยาม คำอธิบาย 1 การบวก 𝐚 + 𝐛 = 〈𝑎1 + 𝑏1, 𝑎2 + 𝑏2, 𝑎3 + 𝑏3〉 2 การคูณเชิง สเกลาร์ 𝑘𝐚 = 〈𝑘𝑎1, 𝑘𝑎2, 𝑘𝑎3〉 3 การเท่ากัน 𝐚 = 𝐛 ดังนั้น 𝑎1 = 𝑏1, 𝑎2 = 𝑏2, 𝑎3 = 𝑏3 4 การติดลบ −𝐛 = (−1)𝐛 = 〈−𝑏1, −𝑏2, −𝑏3〉 5 ผลต่าง 𝐚 − 𝐛 = 𝐚 + (−𝐛) = 〈𝑎1 − 𝑏1, 𝑎2 − 𝑏2, 𝑎3 − 𝑏3, 〉 6 เวกเตอร์ศูนย์ 𝟎 = 〈0,0,0〉 7 ขนาด เวกเตอร์ ‖𝐚‖ = √𝑎1 2 + 𝑎2 2 + 𝑎3 2 ถ้าเวกเตอร์ 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ และ 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ เป็นเวกเตอร์ตำแหน่งของจุดพิกัด 𝑃1(𝑥1, 𝑦1, 𝑧1) และ 𝑃2(𝑥1, 𝑦1, 𝑧1) ดังนั้นเราจะได้เวกเตอร์ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ โดยที่มีความสัมพันธ์เป็นดังสมการที่ 1.15 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ = 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ − 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ = 〈𝑥2 − 𝑥1, 𝑦2 − 𝑦1, 𝑧2 − 𝑧1, 〉 (1.15) สำหรับเวกเตอร์ในสองมิติ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ สามารถกำหนดได้โดยให้จุดเริ่มต้นของเวกเตอร์เป็นจุด 𝑃1 และ จุดปลายของเวกเตอร์เป็นจุด 𝑃2 และสามารถนำมาเป็นเวกเตอร์ตำแหน่ง 𝑂𝑃 ⃗⃗⃗⃗⃗ โดยเวกเตอร์นี้จะมี จุดปลายอยู่ที่ 𝑃(𝑥2 − 𝑥1, 𝑦2 − 𝑦1, 𝑧2 − 𝑧1, ) โดยความสัมพันธ์ของสมการที่ 1.15 สามารถแสดงเป็นเวกเตอร์ดังภาพที่ 1.21
- 22. 21 ภาพที่ 1.21 เวกเตอร์ 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ และ 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ ตัวอย่างที่ 1.10 กำหนดให้จุด 𝑃1 และ 𝑃2 มีพิกัด 𝑃1(4,6, −2) และ 𝑃2(1,8,3) ตามลำดับ จงหาเวกเตอร์ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ วิธีทำ กำหนดให้จุด 𝑃1 มีเวกเตอร์ตำแหน่งเป็น 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ = 〈4,6, −2〉 กำหนดให้จุด 𝑃2 มีเวกเตอร์ตำแหน่งเป็น 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ = 〈1,8,3〉 ใช้สมการที่ 1.15 จงหาเวกเตอร์ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ ได้เป็น 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ = 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ − 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ = 〈1 − 4,8 − 6,3 − (−2)〉 = 〈−3,2,5〉 ตอบ ตัวอย่างที่ 1.11 กำหนดให้เวกเตอร์ 𝐚 = 〈−2,3,6〉 จงหาเวกเตอร์หนึ่งหน่วย วิธีทำ การหาเวกเตอร์หนึ่งหน่วยสามารถหาได้ตามสมการที่ 1.5 โดยมีความสัมพันธ์เป็น 𝐮 = 𝐚 ‖𝐚‖ สามารถหาขนาดของเวกเตอร์ 𝐚 จากตารางที่ 1.4 นิยามที่ 1.2 ข้อ 7 ‖𝐚‖ = √𝑎1 2 + 𝑎2 2 + 𝑎3 2 = √(−2)2 + 32 + 62 = √4 + 9 + 36 = √49 = 7 แทนค่า ‖𝐚‖ = 7 ลงในสมการที่ 1.5 ได้เป็น
- 23. 22 𝐚 ‖𝐚‖ = 〈−2,3,6〉 7 = 1 7 〈−2,3,6〉 = 〈 1 7 (−2), 1 7 3, 1 7 6〉 ∴ 𝐮 = 〈− 2 7 , 3 7 , 6 7 〉 ตอบ 7. เวกเตอร์ 𝐢, 𝐣 และ 𝐤 เวกเตอร์ในสามมิติประกอบด้วยแกน 𝑥, 𝑦 และ 𝑧 ตั้งฉากซึ่งกันและกัน ในแต่ละแกนนั้น ประกอบไปด้วยผลคูณเชิงสเกลาร์ระหว่างปริมาณกับเวกเตอร์หนึ่งหน่วยซึ่งมีทิศทางเดียวกับแกนนั้น ๆ โดยที่เวกเตอร์หนึ่งหน่วยซึ่งมีทิศทางเดียวกับแกน 𝑥 มีชื่อว่า เวกเตอร์ 𝐢 ลำดับต่อมาในส่วนของ แกน 𝑦 มีชื่อว่า เวกเตอร์ 𝐣 และลำดับสุดท้ายในส่วนของแกน 𝑧 มีชื่อว่า เวกเตอร์ 𝐤 ตามลำดับ ดังนั้นการใช้เวกเตอร์ 𝐢, 𝐣, 𝐤 เพื่อแสดงปริมาณเวกเตอร์ 𝐚 ถูกกำหนดให้เป็นไปตามสมการที่ 1.16 𝐚 = 𝑎1𝐢 + 𝑎2𝐣 + 𝑎3𝐤 (1.16) ผลคูณจุด ผลคูณจุด (dot product) เป็นการนำเวกเตอร์สองเวกเตอร์มาดำเนินการคูณกัน โดยให้ ผลลัพธ์เป็นสเกลาร์ ซึ่งในภาษาอังกฤษอาจเรียก inner product หรือ scalar product ผลคูณจุด ใช้สัญกรณ์ “จุด” หรือ “∙” เพื่อดำเนินการ เช่น ผลคูณจุดระหว่างเวกเตอร์ 𝐚 และ 𝐛 ใช้สัญกรณ์ เป็น 𝐚 ∙ 𝐛 กำหนดให้นิยามผลคูณจุดระหว่างสองเวกเตอร์มีนิยามเป็นดังตารางที่ 1.5 ตารางที่ 1.5 นิยามผลคูณจุด นิยามที่ 1.3 ผลคุณจุดระหว่างสองเวกเตอร์ กำหนดให้เวกเตอร์ในสองมิติคือ 𝐚 = 〈𝑎1, 𝑎2〉 และ 𝐛 = 〈𝑏1, 𝑏2〉 𝐚 ∙ 𝐛 = 𝑎1𝑏1 + 𝑎2𝑏2 กำหนดให้เวกเตอร์ในสามมิติคือ 𝐚 = 〈𝑎1, 𝑎2, 𝑎3〉 และ 𝐛 = 〈𝑏1, 𝑏2, 𝑏3〉 𝐚 ∙ 𝐛 = 𝑎1𝑏1 + 𝑎2𝑏2 + 𝑎3𝑏3
- 24. 23 ตัวอย่างที่ 1.12 กำหนดให้ 𝐚 = 10𝐢 + 2𝐣 − 6𝐤 และ 𝐛 = − 1 2 𝐢 + 4𝐣 − 3𝐤 จงหาผลคูณจุด วิธีทำ สามารถดำเนินการหาผลคูณจุดโดยใช้ตารางที่ 1.5 นิยามที่ 1.3 เวกเตอร์ในสามมิติ 𝐚 ∙ 𝐛 = (10) (− 1 2 ) + (2)(4) + (−6)(−3) = − 10 2 + 8 + 18 = −5 + 8 + 18 = 21 ตอบ ตัวอย่างที่ 1.13 กำหนดให้เวกเตอร์หนึ่งหน่วยในสามมิติ เป็นเวกเตอร์ซึ่งมีทิศทางเดียวกับ แกนนั้น ๆ โดยที่เวกเตอร์หนึ่งหน่วยซึ่งมีทิศทางเดียวกับแกน 𝑥, 𝑦, 𝑧 โดยเป็นเวกเตอร์ 𝐢, 𝐣, 𝐤 ซึ่งมีองค์ประกอบเป็น 𝐢 = 〈1,0,0〉 , 𝐣 = 〈0,1,0〉 และ 𝐤 = 〈0,0,1〉 จงแสดงผลคูณจุดระหว่างเวกเตอร์ 𝐢, 𝐣, 𝐤 วิธีทำ 𝐢 ∙ 𝐣 = 𝐣 ∙ 𝐢 = 0, 𝐣 ∙ 𝐤 = 𝐤 ∙ 𝐣 = 0 และ 𝐤 ∙ 𝐢 = 𝐢 ∙ 𝐤 = 0 และ 𝐢 ∙ 𝐢 = 1, 𝐣 ∙ 𝐣 = 1 และ 𝐤 ∙ 𝐤 = 1 ตอบ 1. คุณสมบัติผลคูณจุด ผลคูณจุดมีคุณสมบัติโดยเป็นไปตามทฤษฎีบทที่ 1.2 ซึ่งแสดงอยู่ในตารางที่ 1.6 ตารางที่ 1.6 ทฤษฎีบทคุณสมบัติผลคูณจุด ทฤษฎีบทที่ 1.2 คุณสมบัติผลคูณจุด 1. 𝐚 ∙ 𝐛 = 0 ถ้า 𝐚 = 0 หรือ 𝐛 = 0 2. 𝐚 ∙ 𝐛 = 𝐛 ∙ 𝐚 commutative law 3. 𝐚 ∙ (𝐛 + 𝐜) = 𝐚 ∙ 𝐛 + 𝐚 ∙ 𝐜 distributive law 4. 𝐚 ∙ (𝑘𝐛) = (𝑘𝐚) ∙ 𝐛 = 𝑘(𝐚 ∙ 𝐛), 𝑘 เป็นสเกลาร์ 5. 𝐚 ∙ 𝐚 ≥ 0 6. 𝐚 ∙ 𝐚 = ‖𝐚‖2
- 25. 24 จากทฤษฎีบทที่ 1.2 ลำดับที่ 6 ของตารางที่ 1.6 𝐚 ∙ 𝐚 = ‖𝐚‖2 สัมพันธ์กับอีกรูปแบบหนึ่งคือ ‖𝐚‖ = √𝐚 ∙ 𝐚 = √𝑎1 2 + 𝑎2 2 + 𝑎3 2 2. ผลคูณจุดรูปแบบใหม่ ผลคูณจุดรูปแบบใหม่ (alternative form of dot product) หรือ รูปแบบทางเลือก เป็นการขยายความสามารถจากผลคูณจุดในแบบเดิมที่ให้ผลลัพธ์เพียงสเกลาร์ตามนิยามดังตารางที่ 1.5 ให้มีความสามารถเพิ่มขึ้นโดยมีการขยายความสัมพันธ์ในเรื่องหาค่ามุมระหว่างเวกเตอร์ได้ โดยค่า มุมนั้นจะอยู่ในรูปแบบสัดส่วนค่ามุมโคไซน์ (cos 𝜃) ค่ามุมระหว่างเวกเตอร์ทั้งสองจะต้องมีค่ามุม ไม่เกิน 180° หรือ 𝜋 rad (0 ≤ 𝜃 ≤ 𝜋) กำหนดให้เวกเตอร์สองเวกเตอร์เป็นเวกเตอร์ ตำแหน่งโดยมีจุดกำเนิดอยู่ในที่เดียวกัน มีชื่อว่าเวกเตอร์𝐚 และ 𝐛 เวกเตอร์ทั้งสองมีค่ามุมอยู่ ระหว่าง 0 ≤ 𝜃 ≤ 𝜋 เราจะได้ผลคูณจุดรูปแบบใหม่ที่มีคุณสมบัติโดยเป็นไปตามทฤษฎีบทที่ 1.3 ซึ่งแสดงอยู่ในตารางที่ 1.7 ตารางที่ 1.7 ทฤษฎีบทสำหรับผลคูณจุดรูปแบบใหม่ ทฤษฎีบทที่ 1.3 ผลคูณจุดรูปแบบใหม่ กำหนดให้ผลคูณจุดระหว่างเวกเตอร์ 𝐚 และ 𝐛 เป็น 𝐚 ∙ 𝐛 = ‖𝐚‖‖𝐛‖ cos 𝜃 เมื่อค่ามุม 𝜃 เป็นมุมระหว่างเวกเตอร์ทั้งสอง 3. เวกเตอร์ตั้งฉาก เวกเตอร์ทั้งสองเวกเตอร์ ได้แก่ เวกเตอร์ 𝐚 และ 𝐛 ถ้าทั้งสองเวกเตอร์มีขนาดเท่ากับ เท่าใดก็ตาม หมายความว่าเวกเตอร์ดังกล่าวไม่เป็นเวกเตอร์ศูนย์ ดังนั้น ‖𝐚‖ และ ‖𝐛‖ > 0 จากรูปแบบทางเลือกใหม่ของผลคูณจุดดังตารางที่ 1.7 กำหนดให้ผลคูณจุดระหว่างเวกเตอร์มีค่าเป็น 𝐚 ∙ 𝐛 > 0 เมื่อมุมระหว่างเวกเตอร์มีค่าเป็นศูนย์ หรือ 𝜃 = 0 𝐚 ∙ 𝐛 > 0 เมื่อมุมระหว่างเวกเตอร์มีค่าเป็นมุมแหลม หรือ 0 < 𝜃 < 𝜋 2 𝐚 ∙ 𝐛 = 0 เมื่อมุมระหว่างเวกเตอร์มีค่าเป็นมุมฉาก หรือ 𝜃 = 𝜋 2 𝐚 ∙ 𝐛 < 0 เมื่อมุมระหว่างเวกเตอร์มีค่าเป็นมุมป้าน หรือ 𝜋 2 < 𝜃 < 𝜋
- 26. 25 𝐚 ∙ 𝐛 < 0 เมื่อมุมระหว่างเวกเตอร์มีค่าเป็นมุมป้าน หรือ 𝜋 2 < 𝜃 < 𝜋 𝐚 ∙ 𝐛 < 0 เมื่อมุมระหว่างเวกเตอร์มีทิศทางตรงข้ามกัน หรือ 𝜃 = 𝜋 จากความสัมพันธ์ดังกล่าวสามารถนำเสนอดังภาพที่ 1.22 ก ถึง จ (ก) (ข) (ค) (ง) (จ) ภาพที่ 1.22 ผลคูณจุดในขณะที่มีค่ามุม 𝜃 แตกต่างกัน (ก) เวกเตอร์มีทิศทางเดียวกัน (ข) เวกเตอร์มีมุมแหลม (ค) เวกเตอร์ตั้งฉากกัน (ง) เวกเตอร์มีมุมป้าน และ(จ) เวกเตอร์มีทิศทางตรงกันข้ามกัน ความสัมพันธ์ของมุมระหว่างเวกเตอร์ทั้งสองที่ได้แสดงดังภาพที่ 1.22 ก ถึง จ สามารถสรุปเป็นทฤษฎี บทที่ 1.4 ดังตารางที่ 1.8 ตารางที่ 1.8 การตั้งฉากกันระหว่างสองเวกเตอร์ ทฤษฎีบทที่ 1.4 กฎเกณฑ์การตั้งฉากกันระหว่างสองเวกเตอร์ เวกเตอร์ที่ไม่ใช่เวกเตอร์ขนาดเป็นศูนย์สองตัว เวกเตอร์ 𝐚 และ เวกเตอร์ 𝐛 นั้นจะตั้งฉากกันได้ ก็ต่อเมื่อเวกเตอร์ 𝐚 ∙ 𝐛 = 0 ตัวอย่างที่ 1.14 กำหนดให้เวกเตอร์ 𝐚 = −3𝐢 − 𝐣 + 4𝐤 และ 𝐛 = 2𝐢 + 14𝐣 + 5𝐤 จงพิจารณาว่าเวกเตอร์ทั้งสองตั้งฉาก กันหรือไม่ วิธีทำ จากทฤษฎีบทที่ 1.4 ของตารางที่ 1.8 ได้กล่าวว่า เวกเตอร์ 𝐚 และ เวกเตอร์ 𝐛 นั้น จะตั้งฉากกันได้ก็ต่อเมื่อเวกเตอร์ 𝐚 ∙ 𝐛 = 0 จะได้ 𝐚 ∙ 𝐛 = 〈−3, −1,4〉〈2,14,5〉 = (−3)(2) + (−1)(14) + (4)(5) = −6 + (−14) + (20) = −20 + 20 = 0
- 27. 26 ดังนั้น เวกเตอร์ 𝐚 ∙ 𝐛 = 0 จึงแสดงได้ว่าเวกเตอร์ 𝐚 และ 𝐛 ตั้งฉากกัน ตอบ จากตัวอย่างที่ 1.14 ที่ได้แสดงเวกเตอร์ตั้งฉากกันข้างต้น ถ้าการดำเนินการของผลคูณจุด ได้ผลออกมาเป็น 𝐚 ∙ 𝐛 ≠ 0 เป็นการแสดงว่าเวกเตอร์ทั้งสองนั้นไม่ตั้งฉากกันโดยสามารถ พิจารณาได้ว่าเวกเตอร์ทั้งสองกระทำมุมกันในลักษณะที่เป็นไปตามภาพที่ 1.22 (ข), (ง) และ (จ) 4. มุมระหว่างเวกเตอร์ หลักการการหามุมระหว่างสองเวกเตอร์ (angle between two vectors) เป็นการใช้ หลักการตามทฤษฎีบทที 1.3 ของตารางที่ 1.7 โดยย้ายข้างสมการของทฤษฎีบทดังกล่าวให้เป็นดัง สมการที่ 1.17 cos 𝜃 = 𝐚 ∙ 𝐛 ‖𝐚‖‖𝐛‖ (1.17) ตัวอย่างที่ 1.15 กำหนดให้เวกเตอร์ 𝐚 = 2𝐢 + 3𝐣 + 𝐤 และ 𝐛 = −𝐢 + 5𝐣 + 𝐤 จงคำนวณหามุมระหว่างเวกเตอร์ทั้งสอง วิธีทำ เราสามารถดำเนินการหามุมระหว่างเวกเตอร์ทั้งสองโดยใช้สมการที่ 1.17 โดยพิจารณาแยกในพจน์เศษคือ 𝐚 ∙ 𝐛 ได้เป็น 𝐚 ∙ 𝐛 = (2)(−1) + (3)(5) + (1)(1) = −2 + 15 + 1 = 14 พิจารณาแยกในพจน์ส่วนคือ ‖𝐚‖‖𝐛‖ ได้เป็น ‖𝐚‖‖𝐛‖ = √22 + 32 + 12√(−1)2 + 52 + 12 = √4 + 9 + 1√1 + 25 + 1 = √14√27 แทนค่า 𝐚 ∙ 𝐛 และ ‖𝐚‖‖𝐛‖ ลงในสมการที่ 1.17 cos 𝜃 = (14) (√14√27) = √42 9
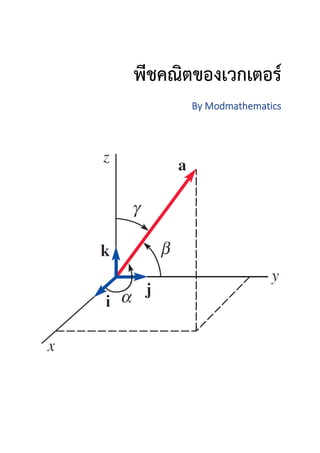
- 28. 27 cos 𝜃 = √42 9 𝜃 = cos−1 0.72 = 43.94° ≈ 43.9° ตอบ 5. โคไซน์แสดงทิศทาง โคไซน์แสดงทิศทาง (direction cosines) เป็นความสัมพันธ์ที่สืบเนื่องมาจากทฤษฎีบท ที่ 1.3 ของตารางที่ 1.7 ซึ่งเป็นความสัมพันธ์ของเวกเตอร์ในสามมิติกับมุมในแต่ละแกนโดยใช้ ประโยชน์จากหลักการหามุมระหว่างเวกเตอร์ของสัดส่วนมุมของโคไซน์ (cosine: cos 𝜃) เทียบกับ แกนต่าง ๆ ในสามมิติ ได้แก่ แกน 𝑥, 𝑦 และ 𝑧 ตามลำดับ โดยที่ในแต่ละแกนนั้นจะมีเวกเตอร์หนึ่ง หน่วยประจำแกน ได้แก่ เวกเตอร์ 𝐢, 𝐣 และ 𝐤 เพื่อแสดงปริมาณเวกเตอร์ เช่น กำหนดให้เวกเตอร์ 𝐚 มีองค์ประกอบเป็น 𝐚 = 𝑎1𝐢 + 𝑎2𝐣 + 𝑎3𝐤 ในสามมิติ และกำหนดให้มุม 𝛼, 𝛽 และ 𝛾 เป็นมุมที่เกิดจากเวกเตอร์ 𝐚 กระทำกับเวกเตอร์หนึ่งหน่วยประจำแกน ได้แก่ เวกเตอร์ 𝐢, 𝐣 และ 𝐤 เรียกสัดส่วนมุมโคไซน์เหล่านี้ว่า โคไซน์แสดงทิศทาง แสดงดังภาพที่ 1.23 ภาพที่ 1.23 โคไซน์แสดงทิศทาง
- 29. 28 โคไซน์แสดงทิศทางของมุม α, β และ γ กำหนดให้เป็นดังสมการที่ 1.18, 1.19 และ 1.20 cos 𝛼 = 𝐚 ∙ 𝐢 ‖𝐚‖‖𝐢‖ (1.18) cos 𝛽 = 𝐚 ∙ 𝐣 ‖𝐚‖‖𝐣‖ (1.19) cos 𝛾 = 𝐚 ∙ 𝐤 ‖𝐚‖‖𝐤‖ (1.20) จัดรูปแบบของสมการให้มีความง่ายขึ้นเนื่องจากในแต่ละแกนมีขนาดเป็นหนึ่งหน่วยจะได้เป็น cos 𝛼 = 𝑎1 ‖𝐚‖ (1.18ก) cos 𝛽 = 𝑎2 ‖𝐚‖ (1.19ก) cos 𝛾 = 𝑎3 ‖𝐚‖ (1.20ก) จากความสัมพันธ์ที่สมการที่ 1.18ก, 1.19ก และ 1.20ก คือ cos 𝛼, cos 𝛽 และ cos 𝛾 ตามลำดับเราจะเรียกความสัมพันธ์เหล่านี้ว่า โคไซน์แสดงทิศทางของเวกเตอร์ 𝐚 โดยเวกเตอร์ 𝐚 นั้น จะต้องไม่มีขนาดเป็นศูนย์ จากความรู้เกี่ยวกับเวกเตอร์หนึ่งหน่วยคือ 𝐮 = 𝐚 ‖𝐚‖ จัดสมการให้มี ความง่ายขึ้นโดยกำหนดให้เป็น 𝐮 = 1 ‖𝐚‖ 𝐚 (1.21) นำมาประยุกต์ใช้กับสมการที่ 1.18ก, 1.19ก และ 1.20ก ได้เป็น cos 𝛼 = 1 ‖𝐚‖ 𝑎1 (1.18ข) cos 𝛽 = 1 ‖𝐚‖ 𝑎2 (1.19ข)
- 30. 29 cos 𝛾 = 1 ‖𝐚‖ 𝑎3 (1.20ข) พิจารณาองค์ประกอบของเวกเตอร์ 𝐚 โดยที่ 𝐚 = 𝑎1𝐢 + 𝑎2𝐣 + 𝑎3𝐤 นำมาพิจารณาใน เทอมเฉพาะของเวกเตอร์หนึ่งหน่วยได้เป็น 1 ‖𝐚‖ 𝐚 = 1 ‖𝐚‖ 𝑎1𝐢 + 1 ‖𝐚‖ 𝑎2𝐣 + 1 ‖𝐚‖ 𝑎3𝐤 (1.22) และ 1 ‖𝐚‖ 𝐚 = (cos 𝛼)𝐢 + (cos β)𝐣 + (cos γ)𝐤 (1.23) ความหมายของเวกเตอร์หนึ่งหน่วย 1 ‖𝐚‖ 𝐚 คือมีขนาดเท่ากับปริมาณขนาดหนึ่งหน่วยดังนั้น cos2 𝛼 + cos2 𝛽 + cos2 𝛾 = 1 (1.24) ตัวอย่างที่ 1.16 กำหนดให้เวกเตอร์ 𝐚 = 2𝐢 + 5𝐣 + 4𝐤 จงคำนวณหาโคไซน์แสดงทิศทางของเวกเตอร์ 𝐚 วิธีทำ ดำเนินการหาขนาดของเวกเตอร์ 𝐚 เป็นอันดับแรกเพื่อนำไปใช้กับสมการที่ 1.18ข, 1.19ข และ1.20ข ได้ออกมาเป็น ‖𝐚‖ = √22 + 52 + 42 = √4 + 25 + 16 = √45 = 3√5 ลำดับต่อมา ดำเนินการแทนค่า ‖𝐚‖ ลงในสมการที่ 1.18ข, 1.19ข และ1.20ข cos 𝛼 = 1 3√5 (2) cos 𝛽 = 1 3√5 (5)
- 31. 30 cos 𝛾 = 1 3√5 (4) ย้ายข้างฟังก์ชันโคไซน์ให้เป็นฟังก์ชันตรีโกณมิติผกผันเพื่อหาทิศทางของมุม 𝛼 = cos−1 2 3√5 𝛽 = cos−1 5 3√5 𝛾 = cos−1 4 3√5 โคไซน์แสดงทิศทางของเวกเตอร์ 𝐚 จะได้เป็น 𝛼 = 72.7° 𝛽 = 41.8° 𝛾 = 53.4° จัดรูปแบบโคไซน์แสดงทิศทางของเวกเตอร์ 𝐚 ให้สอดคล้องกับสมการที่ 1.24 cos2 𝛼 + cos2 𝛽 + cos2 𝛾 = 1 ดังนั้นจะได้ความสัมพันธ์เป็น 4 45 + 25 45 + 16 45 = 1 ตอบ 6. องค์ประกอบเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 ทฤษฎีบทที่ 1.2 ของตารางที่ 1.6 ข้อ 3 ได้แสดงเกี่ยวกับ distributive law คือ 𝐚 ∙ (𝐛 + 𝐜) = 𝐚 ∙ 𝐛 + 𝐚 ∙ 𝐜 ถ้านำหลักการดังกล่าวมาขยายความองค์ประกอบเวกเตอร์ 𝐚 โดยที่ 𝐚 = 𝑎1𝐢 + 𝑎2𝐣 + 𝑎3𝐤 ในเทอมความหมายของผลคูณจุดด้านขวามือของ องค์ประกอบเวกเตอร์จะได้เป็นดังสมการที่ 1.25ก, 1.25ข และ1.25ค 𝑎1 = 𝐚 ∙ 𝐢 (1.25ก) 𝑎2 = 𝐚 ∙ 𝐣 (1.25ข) 𝑎3 = 𝐚 ∙ 𝐤 (1.25ค)
- 32. 31 องค์ประกอบเหล่านี้สามารถแสดงออกมาในเชิงสัญลักษณ์ได้เป็น comp𝐢𝐚 = 𝐚 ∙ 𝐢 (1.26ก) comp𝐣𝐚 = 𝐚 ∙ 𝐣 (1.26ข) comp𝐤𝐚 = 𝐚 ∙ 𝐤 (1.26ค) จากสมการที่ 1.26ก, 1.26ข และ1.26ค เหล่านี้ส่งผลให้เราสามารถที่จะนำไปสู่การหาองค์ประกอบ ของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 ดังภาพที่ 1.24 ภาพที่ 1.24 องค์ประกอบของเวกเตอร์ a บนเวกเตอร์ b จากภาพที่ 1.24 การหาองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 สามารถหาได้ดังสมการที่ 1.27 comp𝐛𝐚 = ‖𝐚‖ cos 𝜃 (1.27) ในกรณีที่การคำนวณหาองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 เมื่อคำนวณออกมาแล้วมีค่า เป็นลบ หรือ comp𝐛𝐚 < 0 เป็นการแสดงว่าองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 มีทิศทางของหัวลูกศรเวกเตอร์อยู่ในทิศทางตรงข้ามกับเวกเตอร์ 𝐛 ซึ่งสามารถบ่งชี้ได้ว่าเวกเตอร์ 𝐚 กางมุมเกิน 90° แต่ไม่เกิน 180° หรือ 𝜋 2 < 𝜃 ≤ 𝜋 ดังภาพที่ 1.25
- 33. 32 ภาพที่ 1.25 องค์ประกอบของเวกเตอร์ a บนเวกเตอร์ b กรณีที่เวกเตอร์ a และเวกเตอร์ b กางมุมระหว่าง 𝜋 2 < 𝜃 ≤ 𝜋 จากภาพที่ 1.25 ซึ่งเป็นกรณีที่เวกเตอร์ a และเวกเตอร์ b กางมุมระหว่าง 𝜋 2 < 𝜃 ≤ 𝜋 เรา สามารถดำเนินการหาองค์ประกอบเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 โดยใช้สมการที่ 1.27 ได้เป็น comp𝐛𝐚 = ‖𝐚‖‖𝐛‖ cos 𝜃 ‖𝐛‖ = 𝐚 ∙ 𝐛 ‖𝐛‖ (1.28) จากสมการที่ 1.28 จะเห็นได้ว่ามีพจน์ในลักษณะเวกเตอร์หนึ่งหน่วยอยู่ในสมการ จัดรูปใหม่ได้เป็น comp𝐛𝐚 = 𝐚 ∙ ( 1 ‖𝐛‖ 𝐛) = 𝐚 ∙ 𝐛 ‖𝐛‖ (1.29) ดังนั้นการหาองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 สามารถหาได้โดยการดำเนินการด้วยผล คูณจุดระหว่างเวกเตอร์ 𝐚 กับเวกเตอร์หนึ่งหน่วยในทิศทางของเวกเตอร์ 𝐛 (Zill, 2018, pp.335) ตัวอย่างที่ 1.17 กำหนดให้เวกเตอร์ 𝐚 = 2𝐢 + 3𝐣 − 4𝐤 และ 𝐛 = 𝐢 + 𝐣 + 2𝐤 จงคำนวณหา comp𝐛𝐚 วิธีทำ เราจะใช้สมการที่ 1.29 ในการคำนวณหา comp𝐛𝐚 อันดับแรกเราจะต้องหา ขนาดของเวกเตอร์ 𝐛 หรือ ‖𝐛‖
- 34. 33 ‖𝐛‖ = √12 + 12 + 22 = √6 ลำดับต่อมานำขนาดของเวกเตอร์ 𝐛 หรือ ‖𝐛‖ ที่ได้มาข้างต้นนำไปคำนวณหา เวกเตอร์หนึ่งหน่วย 1 ‖𝐛‖ 𝐛 = 1 √6 (𝐢 + 𝐣 + 2𝐤) ดังนั้นเราสามารถหา comp𝐛𝐚 ได้โดยการแทนค่าเหล่านี้ลงในสมการที่ 1.29 comp𝐛𝐚 = (2𝐢 + 3𝐣 − 4𝐤) ∙ 1 √6 (𝐢 + 𝐣 + 2𝐤) = − 3 √6 ตอบ 7. จุดฉายของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 จุดฉาย (projection) ของเวกเตอร์ 𝐚 บนทิศทางตามแกนในสามมิติ ซึ่งมีเวกเตอร์หนึ่ง หน่วยในทิศทางแกนต่าง ๆ ได้แก่ เวกเตอร์ 𝐢, 𝐣 และ 𝐤 เมื่อเวกเตอร์ 𝐚 ได้ดำเนินการผลคูณจุดใน ลักษณะของการหาองค์ประกอบเวกเตอร์ 𝐚 กับเวกเตอร์ 𝐢, 𝐣 และ 𝐤 เราจะได้จุดฉายของเวกเตอร์ 𝐚 ดังภาพที่ 1.26 ภาพที่ 1.26 จุดฉายของเวกเตอร์ 𝐚
- 35. 34 จากภาพที่ 1.26 เป็นการแสดงจุดฉายของเวกเตอร์ 𝐚 ไปตามแนวทิศทางต่าง ๆ ในสามมิติโดยอาศัย หลักการผลคูณจุดประกอบด้วยเวกเตอร์ 𝐢, 𝐣 และ 𝐤 เช่น เวกเตอร์ 𝐚 กับทิศทางตามแนวแกน 𝑥 จะได้เป็น proj𝐢𝐚 = (comp𝐢𝐚)𝐢 = (𝐚 ∙ 𝐢)𝐢 = a1𝐢 จากหลักการข้างต้นเราสามารถหาจุดฉายของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 ดังภาพที่ 1.27 ภาพที่ 1.27 จุดฉายของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 จากภาพที่ 1.27 สามารถหาจุดฉายของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 ดังสมการที่ 1.30 proj𝐛𝐚 = (comp𝐛𝐚) ( 1 ‖𝐛‖ 𝐛) = ( 𝐚 ∙ 𝐛 𝐛 ∙ 𝐛 ) 𝐛 (1.30)
- 36. 35 ตัวอย่างที่ 1.18 กำหนดให้เวกเตอร์ 𝐚 = 4𝐢 + 𝐣 และ 𝐛 = 2𝐢 + 3𝐣 จงคำนวณหาจุดฉาย ของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 หรือ proj𝐛𝐚 พร้อมทั้งพล๊อตกราฟแสดง วิธีทำ อันดับแรกให้คำนวณหาองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 โดยใช้สมการที่ 1.29 ในการคำนวณซึ่งจะต้องหาขนาดของเวกเตอร์ 𝐛 เสียก่อนดังนั้น ‖𝐛‖ จะได้เป็น ‖𝐛‖ = √22 + 3𝟐 = √13 คำนวณหาองค์ประกอบของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 ได้เป็น comp𝐛𝐚 = (4𝐢 + 𝐣) ∙ 1 √13 (2𝐢 + 3𝐣) = 11 √3 นำสิ่งที่คำนวณได้ข้างต้นแทนค่าลงในสมการที่ 1.30 เพื่อคำนวณหาจุดฉายของเวกเตอร์ 𝐚 บนเวกเตอร์ 𝐛 หรือ proj𝐛𝐚 proj𝐛𝐚 = ( 11 √3 ) ( 1 √13 ) (2𝐢 + 3𝐣) = 22 13 𝐢 + 33 13 𝐣 นำค่า proj𝐛𝐚 = 22 13 𝐢 + 33 13 𝐣 ไปพล๊อตกราฟแสดงได้ดังภาพที่ 1.28 ภาพที่ 1.28 ผลการหาจุดฉาย proj𝐛𝐚
- 37. 36 8. การประยุกต์ใช้ผลคูณจุดกับฟิสิกส์กลศาสตร์ กำหนดให้เวกเตอร์มีปริมาณและทิศทางโดยใช้ชื่อว่าเวกเตอร์ 𝐹 ลากเลื่อนวัตถุจนเกิด การเคลื่อนที่ในระยะทางเท่ากับ 𝑑 เมื่อกำหนดให้งานที่เกิดขึ้นเป็น 𝑊 = 𝐹𝑑 หากแรง 𝐅 กระทำ ต่อวัตถุเป็นมุม 𝜃 ในทิศทางการเคลื่อนที่ ดังนั้นงานที่เกิดขึ้นโดยแรง 𝐅 ถูกกำหนดให้เป็นผลคูณของ ส่วนประกอบของ 𝐅 ในทิศทางของการกระจัดและระยะทาง ‖𝐝‖ โดยสามารถพิจารณาได้โดย เริ่มต้นจากงานมีค่าเท่ากับ 𝑊 = 𝐹 ∙ 𝑑 แทนค่าในแต่ละปริมาณ เช่น 𝐹 = ‖𝐅‖ cos 𝜃 และ 𝑑 = ‖𝐝‖ 𝑊 = (‖𝐅‖ cos 𝜃)(‖𝐝‖) จัดรูปสมการให้สอดคล้องกับผลคูณจุดผลคูณจุดรูปแบบใหม่ คือ 𝐚 ∙ 𝐛 = ‖𝐚‖‖𝐛‖ cos 𝜃 𝑊 = ‖𝐅‖‖𝐝‖ cos 𝜃 ความสัมพันธ์ดังกล่าวจะสอดคล้องกับภาพที่ 1.29 ภาพที่ 1.29 งานที่เกิดขึ้นจาก 𝑊 = ‖𝐅‖‖𝐝‖ cos 𝜃
- 38. 37 ถ้าแรง 𝐅 ก่อให้เกิดการเคลื่อนที่ของวัตถุดังภาพที่ 1.29 ส่งผลให้เกิดงาน คือ 𝑊 = 𝐅 ∙ 𝐝 งานที่เกิดขึ้นมานั้นเกิดจากผลคูณจุดซึ่งให้ผลเป็นสเกลาร์ดังนั้นงานจึงเป็นปริมาณสเกลาร์ด้วยเช่นกัน ตัวอย่างที่ 1.19 กำหนดให้แรง 𝐅 มีเวกเตอร์เป็น 𝐅 = 2𝐢 + 4𝐣 แรงดังกล่าวนี้ส่งผลต่อการ เคลื่อนที่จากจุดเริ่มต้นคือ 𝑃1(1,1) เคลื่อนที่ไปสู่จุดปลายคือจุด 𝑃2(4,6) จงคำนวณหางาน โดยกำหนดให้ขนาดของแรง 𝐅 หรือ ‖𝐅‖ มีหน่วยเป็นนิวตัน และระยะทาง 𝐝 หรือ ‖𝐝‖ มีหน่วย เป็นเมตร วิธีทำ คำนวณหาระยะทางระหว่างพิกัดจุด 𝑃1 ถึง 𝑃2 มีหลักการคล้ายกับการหาเวกเตอร์จุดต้น จุดปลายหรือ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ คำนวณออกมาได้เป็น 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ = 𝑂𝑃2 ⃗⃗⃗⃗⃗⃗⃗ − 𝑂𝑃1 ⃗⃗⃗⃗⃗⃗⃗ = 〈4,6〉 − 〈1,1〉 = (4𝐢 + 6𝐣) − (𝐢 + 𝐣) = 4𝐢 + 6𝐣 − 𝐢 − 𝐣 = 3𝐢 + 5𝐣 ระยะระหว่างพิกัดจุด 𝑃1 ถึง 𝑃2 หรือ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ คือ ระยะทาง 𝐝 หรือ ‖𝐝‖ 𝐝 = 3𝐢 + 5𝐣 ดังนั้นคำนวณหางานได้เป็น 𝑊 = (2𝐢 + 4𝐣 ) ∙ (3𝐢 + 5𝐣) = 26 นิวตันเมตร ตอบ ผลคูณไขว้ ผลคูณไขว้ (cross product) โดยทั่วไปนิยมเรียกทับศัพท์ว่า “ครอสโปรดักส์” เป็นเนื้อหาที่ สำคัญที่สุดของบทเรียนพีชคณิตของเวกเตอร์ในสามมิติของเอกสารประกอบการสอนเล่มนี้ เนื่องจาก ต้องใช้ทักษะคณิตศาสตร์หลายเรื่อง เช่น ตัวกำหนด (determinant) ไมเนอร์ (minor) และโคแฟก เตอร์ (co-factor) เป็นต้น ซึ่งทักษะเหล่านี้มีจุดประสงค์เพียงเพื่อให้ได้มาซึ่งผลการคูณไขว้เท่านั้นและ มิได้ต้องการสืบทราบที่มาและขั้นตอนของเรื่องราวเหล่านี้ ดังนั้นหัวข้อผลคูณไขว้ที่กำลังจะดำเนิน
- 39. 38 เรื่องราวการอธิบายไปจะเป็นการนำเสนอเข้ามาและใช้งานในทันทีถ้าผู้เรียนมีความสนใจใน รายละเอียดเชิงลึกซึ้งสามารถศึกษาได้ใน บทเรียน 8.4 Determinants (Zill, 2018, pp.393) 1. รูปแบบองค์ประกอบของผลคูณไขว้ ผลคูณไขว้ใช้สัญกรณ์ “คูณ” หรือ “×” (times) เพื่อดำเนินการ เช่น ผลคูณไขว้ ระหว่างเวกเตอร์ 𝐚 และ 𝐛 ใช้สัญกรณ์เป็น 𝐚 × 𝐛 นิยมอ่านว่า “เวกเตอร์-เอ-ครอส-บี” กำหนดให้นิยามผลคูณไขว้ระหว่างสองเวกเตอร์มีนิยามเป็นดังตารางที่ 1.9 ตารางที่ 1.9 นิยามผลคูณไขว้ นิยามที่ 1.4 ผลคูณไขว้ของสองเวกเตอร์ ผลคูณไขว้ของสองเวกเตอร์ซึ่งประกอบด้วยเวกเตอร์ 𝐚 = 〈𝑎1, 𝑎2, 𝑎3〉 และเวกเตอร์ b= 〈𝑏1, 𝑏2, 𝑏3〉 จะใช้สัญลักษณ์ผลคูณไขว้เป็น 𝐚 × 𝐛 โดยมีองค์ประกอบเป็น 𝐚 × 𝐛 = (𝑎2𝑏3 − 𝑎3𝑏2)𝐢 − (𝑎1𝑏3 − 𝑎3𝑏1)𝐣 + (𝑎1𝑏2 − 𝑎2𝑏1)𝐤 พบว่าผลคูณไขว้จากนิยามที่ 1.4 มีผลลัพธ์ออกมาเป็นปริมาณเวกเตอร์ และกระบวณการคำนวณที่ เกิดขึ้นในนิยามที่ 1.4 เป็นผลมาจากการดำเนินการระหว่างเวกเตอร์ด้วยหลักการ “ตัวกำหนด” โดยมี รายละเอียดคือ 𝐚 × 𝐛 = | 𝐢 𝐣 𝐤 𝑎1 𝑎2 𝑎3 𝑏1 𝑏2 𝑏3 | = | 𝑎2 𝑎3 𝑏2 𝑏3 | 𝐢 − | 𝑎1 𝑎3 𝑏1 𝑏3 | 𝐣 + | 𝑎1 𝑎2 𝑏1 𝑏2 | 𝐤 = (𝑎2𝑏3 − 𝑎3𝑏2)𝐢 − (𝑎1𝑏3 − 𝑎3𝑏1)𝐣 +(𝑎1𝑏2 − 𝑎2𝑏1)𝐤 ซึ่งสอดคล้องกับหลักการหาตัวกำหนด ไมเนอร์ และโคแฟกเตอร์ นันเอง
- 40. 39 ตัวอย่างที่ 1.20 กำหนดให้เวกเตอร์ 𝐚 = 4𝐢 − 2𝐣 + 5𝐤 และ 𝐛 = 3𝐢 + 𝐣 − 𝐤 จงคำนวณหาผลคูณไขว้ระหว่างเวกเตอร์ 𝐚 × 𝐛 วิธีทำ 𝐚 × 𝐛 = | 𝐢 𝐣 𝐤 4 −2 5 3 1 −1 | = | −2 5 1 −1 | 𝐢 − | 4 5 3 −1 | 𝐣 + | 4 −2 3 1 | 𝐤 = ((−2)(−1) − (1)(5))𝐢 − ((4)(−1) − (3)(5))𝐣 +((4)(1) − (3)(−2))𝐤 = −3𝐢 + 19𝐣 + 10𝐤 ตอบ 2. คุณสมบัติของผลคูณไขว้ ผลคูณไขว้ของสองเวกเตอร์สามารถสรุปเป็นคุณสมบัติได้ดังตารางที่ 1.10 ดังนี้ ตารางที่ 1.10 ตารางสรุปคุณสมบัติผลคูณไขว้ ทฤษฎีบทที่ 1.5 คุณสมบัติของผลคูณไขว้ 1. 𝐚 × 𝐛 = 0 ถ้า 𝐚 = 0 หรือ 𝐚 = 0 2. 𝐚 × 𝐛 = −𝐛 × 𝐚 3. 𝐚 × (𝐛 + 𝐜) = (𝐚 × 𝐛) + (𝐚 × 𝐜) distributive law 4. (𝐚 + 𝐛) × 𝐜 = (𝐚 × 𝐜) + (𝐛 × 𝐜) distributive law 5. 𝐚 × (𝑘𝐛) = (𝑘𝐚) × 𝐛 = 𝑘(𝐚 × 𝐛), 𝑘 เป็นสเกลาร์ 6. 𝐚 × 𝐚 = 0 7. 𝐚 ∙ (𝐚 × 𝐛) = 0 8. 𝐛 ∙ (𝐚 × 𝐛) = 0
- 41. 40 3. กฎมือขวา กฎมือขวา (right-hand rule) เป็นการใช้มือข้างขวาของตัวเองโดยตัวผู้ใช้มองที่มือข้าง ขวาของตัวเองโดยกางมือและกำมือเป็นไปตามลักษณะดังภาพที่ 1.30 และ 1.31 โดยจะต้องคำนึงถึง ลำดับการหาผลคูณไขว้ของเวกเตอร์ตัวหน้ากับตัวหลังจะต้องไม่สลับกัน โดยให้เวกเตอร์ตัวหน้าอยู่ใน ท่ากางปลายนิ้วมือทั้งสี่เหยียดให้ตรงเสียก่อนแล้วจึงให้ทำท่ากำมือตามแนวกระทำกันของมุมเป็น เวกเตอร์ในลำดับตัวหลังของผลคูณไขว้ ภาพที่ 1.30 กฎมือขวา กรณี 𝐚 × 𝐛 ภาพที่ 1.31 กฎมือขวา กรณี 𝐛 × 𝐚
- 42. 41 ผลการคูณไขว้ระหว่าง 𝐚 × 𝐛 ให้เวกเตอร์ลัพธ์ในทิศทางของนิ้วโป้งดังภาพที่ 1.30 ซึ่งให้ผล เวกเตอร์ลัพธ์แตกต่างจาก ผลการคูณไขว้ระหว่าง 𝐛 × 𝐚 ซึ่งให้เวกเตอร์ลัพธ์ในทิศทางของนิ้วโป้ง ดังภาพที่ 1.31 ข้อสังเกตดังกล่าวสอดคล้องกับทฤษฎีบทที่ 1.5 ของตารางที่ 1.10 ข้อ 2. นั่นเอง 4. ผลคูณไขว้รูปแบบใหม่ กำหนดให้ผลคูณไขว้รูปแบบใหม่ (alternative form) มีรูปแบบดังนี้ คือ 𝐚 × 𝐛 = (‖𝐚‖‖𝐛‖ sin 𝜃)𝐧 โดยเวกเตอร์ 𝐚 และ 𝐛 เป็นเวกเตอร์ในสามมิติ และ เวกเตอร์หนึ่งหน่วย 𝐧 เป็น เวกเตอร์ขนาดหนึ่งหน่วยที่ตั้งฉากกับ แผ่นระนาบที่มีเวกเตอร์ 𝐚 และ 𝐛 ประกอบอยู่ด้วยกัน บางครั้งเราอาจเรียกเวกเตอร์ 𝐧 นี้ว่า เวกเตอร์ปกติ (normal vector) 5. เวกเตอร์ขนานกัน เวกเตอร์ที่มคุณสมบัติขนานกัน (parallel vector) สามารถพิจารณาโดยการใช้ผลคูณ ไขว้พิจารณาทั้งสองเวกเตอร์โดยที่เมื่อผลคูณไขว้ได้ผลเป็น 0 ดังทฤษฎีบทที่ 1.7 ของตารางที่ 1.11 ตารางที่ 1.11 การขนานกันของเวกเตอร์ ทฤษฎีบทที่ 1.7 กฎเกณฑ์การขนานกันของเวกเตอร์ เวกเตอร์สองเวกเตอร์ที่ไม่เป็นเวกเตอร์ศูนย์ เวกเตอร์ 𝐚 และ 𝐛 ขนานกันเมื่อ 𝐚 × 𝐛 = 𝟎 จากสมการผลคูณไขว้รูปแบบใหม่ที่ได้กล่าวถึงนั่นคือ 𝐚 × 𝐛 = (‖𝐚‖‖𝐛‖ sin 𝜃)𝐧 พบว่า มุมระหว่างเวกเตอร์ 𝐚 และ 𝐛 จะขนานกันตามทฤษฎีบทที่ 1.7 ของตารางที่ 1.12 𝐚 × 𝐛 = 𝟎 เมื่อมุม 𝜃 = 0 หรือมุม 𝜃 = 𝜋 ตัวอย่างที่ 1.21 กำหนดให้เวกเตอร์ 𝐚 = 2𝐢 + 𝐣 − 𝐤 และ 𝐛 = −6𝐢 − 3𝐣 + 3𝐤 จงแสดงว่าเวกเตอร์ทั้งสองขนานกันหรือไม่
- 43. 42 วิธีทำ 𝐚 × 𝐛 = | 𝐢 𝐣 𝐤 2 1 −1 −6 −3 3 | = | 1 −1 −3 3 | 𝐢 − | 2 −1 −6 3 | 𝐣 + | 2 1 −6 −3 | 𝐤 = ((1)(3) − (−3)(−1))𝐢 − ((2)(3) − (−6)(−1))𝐣 +((2)(−3) − (−6)(1))𝐤 = (3 − 3)𝐢 − (6 − 6)𝐣 + (−6 + 6)𝐤 = 0𝐢 − 0𝐣 + 0𝐤 = 𝟎 ตอบ เวกเตอร์ 𝐚 และ 𝐛 ขนานกันเพราะ 𝐚 × 𝐛 = 𝟎 6. ผลคูณแบบพิเศษ ผลคูณแบบพิเศษ (special product) เป็นการผสมผสานของการดำเนินการผลคูณจุด และผลคูณไขว้โดยกำหนดให้ ผลคูณแบบพิเศษแบบที่ 1 คือ 𝐚 ∙ (𝐛 × 𝐜) เรียกว่า ผลคูณสเกลาร์ สามชั้น (scalar triple product) โดยที่ผลคูณแบบพิเศษแบบที่ 1 นั้นสามารถดำเนินการได้เป็น 𝐚(𝐛 × 𝐜) = | 𝑎1 𝑎2 𝑎3 𝑏1 𝑏2 𝑏3 𝑐1 𝑐2 𝑐3 | จากการดำเนินการข้างต้นเราสามารถสรุปคุณสมบัติผลคูณแบบพิเศษแบบที่ 1 ได้เป็น 𝐚 ∙ (𝐛 × 𝐜) = (𝐚 × 𝐛) ∙ 𝐜
- 44. 43 ผลคูณแบบพิเศษแบบที่ 2 คือ 𝐚 × (𝐛 × 𝐜) เรียกผลคูณนี้ว่า ผลคูณสามเวกเตอร์ (vector triple product) โดยมีคุณสมบัติเป็น 𝐚 × (𝐛 × 𝐜) = (𝐚 ∙ 𝐜)𝐛 − (𝐚 ∙ 𝐛)𝐜 7. การหาพื้นที่ การหาพื้นที่ (area) เราสามารถใช้ผลคูณเวกเตอร์เพื่อดำเนินการหาพื้นที่ได้ โดยเวกเตอร์ ทั้งสองจะต้องไม่เป็นเวกเตอร์ศูนย์ เราสามารถหาพื้นที่ (𝐴) ของสี่เหลี่ยมด้านขนาน คือ 𝐴 = (ฐาน)(สูง) การหาพื้นที่ (𝐴) ของสี่เหลี่ยมด้านขนานสามารถแสดงได้ดังภาพที่ 1.32 ภาพที่ 1.32 พื้นที่ (𝐴) ของสี่เหลี่ยมด้านขนาน ซึ่งเราจะเห็นได้ว่า 𝐴 = ‖𝐛‖(‖𝐚‖ sin 𝜃) และจัดรูปได้เป็น 𝐴 = ‖𝐚‖‖𝐛‖ sin 𝜃 หรือพิจารณาด้วยผลคูณไขว้ได้เป็น 𝐴 = ‖𝐚 × 𝐛‖ ในทำนองเดียวกันกับภาพที่ 1.33 เราสามารถหาพื้นที่ (𝐴) ของสามเหลี่ยมที่ประกอบด้วย ด้าน 𝑎 และ 𝑏 โดยได้เป็น
- 45. 44 ภาพที่ 1.33 พื้นที่ (𝐴) ของสามเหลี่ยมที่ประกอบด้วยด้าน 𝑎 และ 𝑏 จากภาพที่ 1.33 พื้นที่ (𝐴) ของสามเหลี่ยมที่ประกอบด้วยด้าน 𝑎 และ 𝑏 มีสมการเป็น 𝐴 = 1 2 ‖𝐚 × 𝐛‖ ตัวอย่างที่ 1.22 กำหนดให้จุดพิกัดในระบบสามมิติได้แก่ จุดพิกัด 𝑃1(1,1,1) , 𝑃2(2,3,4) และ 𝑃3(3,0, −1) จงใช้ข้อมูลจากจุดพิกัดดังกล่าวแสดงวิธีการคำนวณหาพื้นที่สามเหลี่ยม วิธีทำ เวกเตอร์ที่กำหนดโดยพิกัด 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ และเวกเตอร์ 𝑃2𝑃3 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ สามารถนำมาใช้เป็นด้านทั้งสองด้าน ของสามเหลี่ยม ซึ่งเวกเตอร์ 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ = 𝐢 + 2𝐣 + 3𝐤 และ 𝑃2𝑃3 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ = 𝐢 − 3𝐣 − 5𝐤 เราจะได้ผลคูณไขว้ออกมาเป็น 𝑃1𝑃2 ⃗⃗⃗⃗⃗⃗⃗⃗ × 𝑃2𝑃3 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ = | 𝐢 𝐣 𝐤 1 2 3 1 −3 −5 | = | 2 3 −3 −5 | 𝐢 − | 1 3 1 −5 | 𝐣 + | 1 2 1 −3 | 𝐤 = −𝐢 + 8𝐣 − 5𝐤 เราจะสามารถหาพื้นที่สามเหลี่ยมได้โดย
- 46. 45 𝐴 = 1 2 ‖−𝐢 + 8𝐣 − 5𝐤‖ = 3 2 √10 ตอบ 8. การหาปริมาตร การหาปริมาตรนี้เกิดขึ้นจากการขนานกันของเวกเตอร์เราอาจเรียกอีกชื่อหนึ่งได้ว่า ปริมาตรของด้านขนาน (volume of a Parallelepiped) ถ้าเวกเตอร์ a, b และ c ไม่อยู่ในระนาบ เดียวกัน ปริมาตรของด้านขนาน ซึ่งมีขอบในแต่ละด้านเป็น a, b และ c แสดงดังภาพที่ 1.34 คือ พิมพ์สมการที่นี่ ภาพที่ 1.34 ปริมาตรของด้านขนาน โดยขอบในแต่ละด้านเป็นด้าน a, b และ c จากภาพที่ 1.34 สามารถแสดงวิธีการหาปริมาตร (𝑉) ได้ออกมาเป็น 𝑉 = (พื้นที่ฐาน)(สูง) = ‖𝐛 × 𝐜‖|comp𝐛×𝐜𝐚| = ‖𝐛 × 𝐜‖ |𝐚 ∙ ( 1 ‖𝐛 × 𝐜‖ 𝐛 × 𝐜)|
- 47. 46 ดังนั้นปริมาตร (𝑉) คือ 𝑉 = |𝐚 ∙ (𝐛 × 𝐜)| ปริมาตร (𝑉) ที่เกิดขึ้นนั้น มาจากการขนานกันของเวกเตอร์ทั้งสาม ซึ่งเกิดขึ้นจากการผสมผสานกัน ระหว่างการดำเนินการผลคูณจุดและผลคูณไขว้ 9. เวกเตอร์โคพลานาร์ เวกเตอร์ที่อยู่ในระนาบร่วมกันเรียกว่า “เวกเตอร์โคพลานาร์” (coplanar vectors) สำหรับในกรณีที่เวกเตอร์ 𝐚, 𝐛 และ 𝐜 เหล่านี้ไม่ใช่เวกเตอร์โคพลานาร์ ผลออกมาจะได้เป็น 𝐚 ∙ (𝐛 × 𝐜) ≠ 0 เนื่องจากปริมาณของ เวกเตอร์ 𝐚, 𝐛 และ 𝐜 เป็นปริมาณเวกเตอร์แสดงด้านขอบในแต่ละมิติซึ่งทั้ง สามล้วนมีปริมาณดังนั้นจึงไม่มีทางที่จะเป็นเวกเตอร์ศูนย์ ดังนั้นการที่จะเป็นเวกเตอร์โคพลานาร์ได้ จะต้องมีคุณสมบัติของสมการเป็น 𝐚 ∙ (𝐛 × 𝐜) = 0 เวกเตอร์ 𝐚, 𝐛 และ 𝐜 เป็นเวกเตอร์โคพลานาร์ โดยที่เวกเตอร์ดังกล่าวอยู่ในระนาบร่วมกัน 10. การประยุกต์ผลคูณไขว้ในความหมายของฟิสิกส์ การประยุกต์เวกเตอร์ในทางฟิสิกส์กำหนดให้ แรง (force) เป็นเวกเตอร์ 𝐅 โดยเป็นแรง กระทำอยู่ที่ด้านปลายของเวกเตอร์ตำแหน่ง 𝐫 แสดงดังภาพที่ 1.35 ภาพที่ 1.35 การประยุกต์ใช้เวกเตอร์ 𝐅 เป็นแรงกระทำ และเวกเตอร์ตำแหน่ง 𝐫