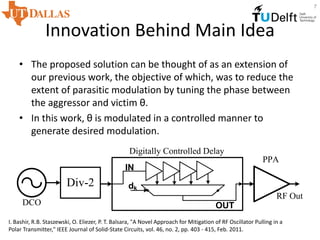
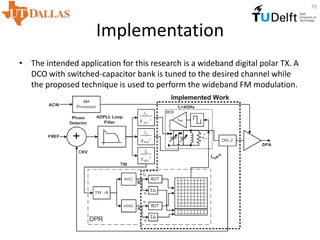
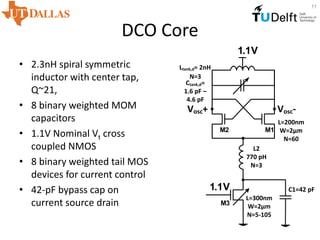
This document proposes a digitally controlled wideband frequency modulator using an injection-locked oscillator with fine frequency resolution. It achieves wideband FM modulation by controlling the phase between a delayed version of the oscillator output signal and the oscillator itself. The key advantages are scalable linear tuning range and fine frequency resolution without requiring large capacitor arrays. Simulation and measurement results show it can achieve frequency steps of 24.8 kHz and an FM range of over 2 GHz by adjusting the injection current ratio.

1. A Digitally Controlled Wideband
Frequency Modulator
I. Bashir, R. B. Staszewski, P. T. Balsara
April 14th, 2016

2. Problem Statement
• Designing a RF oscillator to modulate wideband FM signals
poses two main challenges: Linearity of the DCO transfer
function and frequency resolution.
2
f0
d
Δf0
f0
d
f0
d
PSD
f
PSD
f
Ideal
Poor
Resolution
Poor
Linearity
BW>5MHz

3. Prior Art
• DCO utilizing switched capacitor array in the LC tank [1] to
modulate its’ frequency has non-linear transfer function over
a wide frequency range.
C.-M. Hung, et. al, "A digitally controlled oscillator system for SAW-less transmitters in cellular handsets,"
IEEE JSSC, vol. 41, no. 5, pp. 1160-1170, May 2006.
tanko C
C
f
f 


3

4. Prior Art
• Capacitive Degeneration in LC-Tank Oscillator
– Pros: Achieves very small step size without requiring ΣΔ
dithering of unit capacitor
– Cons: Phase noise degradation with large capacitor arrays,
limited linear tuning range
L. Fanori, et. al, "Capacitive Degeneration in LC-Tank Oscillator for DCO Fine-Frequency Tuning," IEEE JSSC,
vol. 45, no. 12, pp. 2737-2745, 2010.
4

5. Prior Art
• Incrementally sized capacitor bank [3]
– Pros: Very small step size ~ 5kHz, monotonic TF
– Cons: Linear FM range 10.2 MHz, requires large number of
capacitor banks for WB modulation
J. Zhuang et al., "A 3.3 GHz LC-based digitally controlled oscillator with 5 kHz frequency resolution," in
Proc. IEEE ASSCC, 2007, pp. 428-431.
5

6. Proposed Solution
• Oscillator is injection locked to a ‘phase delayed’ version of its’ output signal.
The output frequency ωout is given by Adler’s eqn.
• A properly calibrated time varying phase ‘θ[k]’ generates the desired FM
modulation. Within a reasonable range of θ around 0◦ generated by the Digital-
Phase Rotator (DPR), ωout increases linearly with θ.
AI
AI
kIkII
ka
kb
k
k
QI
I
k
u
u
injinjinj
o
o
osc
inj
out






31~
61~
][][
][
][
tan][
])[sin(
2
][
2
2
2
1
1




(wide-band FM)
(narrow-band FM)
LSB
ωout
Scalable linear tuning
range
τc
DPR
a b
0º
≈ 90º
τf
Iosc
+
Vosc
-
DCO
Iinj1
Iinj2
a·Iu
b·Iu
Iosc
Iinj1
Iinj2
0º-45º 45º
Iinjejθ
(Adler’s Eq.)
6
I. Bashir, R.B. Staszewski, P. T. Balsara, "A Digitally Controlled Injection-Locked Oscillator with Fine Frequency
Resolution," IEEE Journal of Solid-State Circuits, vol. 51, no. 6, pp. xxx-xxx, June 2016. (published)

7. Innovation Behind Main Idea
• The proposed solution can be thought of as an extension of
our previous work, the objective of which, was to reduce the
extent of parasitic modulation by tuning the phase between
the aggressor and victim θ.
• In this work, θ is modulated in a controlled manner to
generate desired modulation.
I. Bashir, R.B. Staszewski, O. Eliezer, P. T. Balsara, "A Novel Approach for Mitigation of RF Oscillator Pulling in a
Polar Transmitter," IEEE Journal of Solid-State Circuits, vol. 46, no. 2, pp. 403 - 415, Feb. 2011.
7
DCO
Div-2 dk
IN
OUT
Digitally Controlled Delay
PPA
RF Out

8. Numerical Modeling of ILO
• Important characteristics of Injection Locked Oscillator (ILO) can be
studied through numerical modeling in MATLAB/Simulink.
(a) (b)
(c) (d)
Iinj
sgn()
R
C
L
-Iosc
X
+
Vosc
- Vosc
Itank
Iosc
Iinj
ϕ(t)
θ(t)
Iinj=Ir*Iosc
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
-120
-80
-40
0
40
80
120
160
Injection Frequency [GHz]
[deg]
Ir
0.5
Ir
0.8
Ir
1.0
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
-360
-270
-180
-90
0
90
180
270
360
[deg]
Injection Frequency [GHz]
Injection Locked
Injection Pulling
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
-50
-30
-10
10
30
50
[deg]


M. Heidari, A. A. Abidi, “Behavioral Models of Frequency Pulling in Oscillators,” Proc. IEEE Int. Behavioral
Modeling and Simulation Workshop (BMAS), pp. 100–104, Sept. 2007.
8

9. Numerical Modeling of IL Oscillator
9
-180 -135 -90 -45 0 45 90 135 180
4300
4350
4400
4450
4500
4550
4600
4650
DCOFrequency[MHz]
Theta [deg]
-180 -135 -90 -45 0 45 90 135 180
0
0.2
0.4
0.6
0.8
1
NormalizedPeakVoltage
DCO Frequency
Peak Voltage
(a) (b)
Iosc
Itank
AuxiliaryLoop
sgn()
Ir· ejθ
+
Io
Ctank
tank
L
1
s
1
dt
d
х
+-
+-
Rtank
gm Differential Pair
LC Tank
Vosc
Iinj
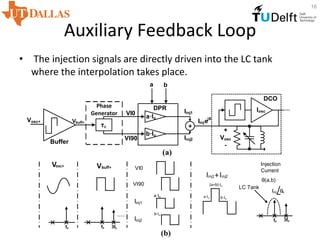
• The conventional model is modified by adding an auxiliary
feedback loop with a controlled delay θ and the resulting transfer
function is simulated in MATLAB/Simulink.
• Desired modulation bandwidth can be achieved by adjusting Ir.
• In order to limit the loss of oscillator amplitude, -45◦ < θ < 45◦.

10. Implementation
• The intended application for this research is a wideband digital polar TX. A
DCO with switched-capacitor bank is tuned to the desired channel while
the proposed technique is used to perform the wideband FM modulation.
10

11. DCO Core
• 2.3nH spiral symmetric
inductor with center tap,
Q~21,
• 8 binary weighted MOM
capacitors
• 1.1V Nominal Vt cross
coupled NMOS
• 8 binary weighted tail MOS
devices for current control
• 42-pF bypass cap on
current source drain
11
1.1V
1.1V
M1M2
M3
Ctank,d=
1.6 pF –
4.6 pF
Ltank,d= 2nH
N=3
Vosc+
L=200nm
W=2μm
N=60
Vosc-
L2
770 pH
N=3
L=300nm
W=2μm
N=5-105
C1=42 pF

12. 1 2 3 4 5 6 7 8 9
0
5
10
15
20
25
Frequency [GHz]
Q
Q vs. Frequency
Qbw
Qconv
Qps
Inductor Design
• P-cell parameters:
Width=12μm, Inner
Radius = 60μm, Turns = 3,
Spacing = 2 μm
• Qbw is calculated by
resonating the inductor
with a shunt capacitor [6]
K. O, "Estimation methods for quality factors of inductors fabricated in silicon integrated circuit process technologies,"
IEEE JSSC, vol. 33, no. 8, pp. 1249-1252, Aug. 1998
12













)Re(Y
)Im(Y
atan
dω
d
2
ω
Q
11
11o
ps
)Re(Z
)Im(Z
Q
diff
diff
conv 
21122211
diff
YYYY
Z


4
)()(
)(2
222113121123
1323
YYYYYY
YY
Zdiff



2-Port Inductor
Model
3-Port Inductor
Model

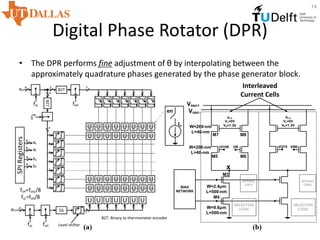
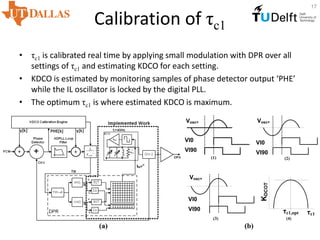
13. Phase Generator (PG) Circuit
• The PG circuit
– Generates approximately quadrature signals for the DPR.
– Sets optimum phase relationship between VI0, VI90, and Vosc as shown
in Fig(b).
(c)
(b)
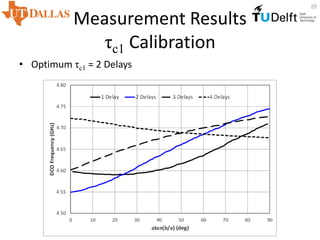
τc1 α1 α2 α1 + α2
Delays [deg] [deg] [deg]
1 194.6 100.5 94.1
2 129.7 35.5 94.1
3 65.8 28.4 94.2
4 2.0 92.1 94.2
V osc +
VI0
VI90
α1 α2
τc1 τc2
VI0
VI90
VI180
VI270
τc1
0: 37ps
1: 52.5ps
2: 72.7ps
3: 83.7ps
τc2
0: 55ps
1: 67ps
2: 80.5ps
3: 89.5ps
dk
IN
OUT
Vosc+
Vosc-
(a)
Vbuff+
Vbuff-
13

14. Digital Phase Rotator (DPR)
• The DPR performs fine adjustment of θ by interpolating between the
approximately quadrature phases generated by the phase generator block.
14
ac
6
B2T
3 7
1 1 1 1 1 1 1
B2T
3
7
1111111
en
U U U U U U U U
U U U U U U U U
U U U U U U U U
U U U U U U U U
U U U U U U U
Iu
af
6
ΣΔ 7
1 1 1 1 1 1 1
fsH
fsH
fsH
fsL
fsL
fsH=fosc/8
fsL=fsH/8
SPIRegisters
ac
6
af
6
bc
6
bf
6
(a) (b)
W=2.4μm
L=500-nm
W=9.6μm
L=500-nm
W=200-nm
L=40-nm
W=200-nm
L=40-nm
VI0VI180
ac,k
VL=0V
VH=1.3V
VI90VI270
bc,k
VL=0V
VH=1.3V
Vosc+
Vosc-
x
SELECTION
LOGIC
BYPASS
CAPS
SELECTION
LOGIC
BYPASS
CAPS
M3
M4
M5 M6
M7 M8
BIAS
NETWORK
Interleaved
Current Cells
B2T: Binary to thermometer encoder
Level shifter

15. MASH ΣΔ
• The MASH ΣΔ drives 7 unit cells to improve the resolution of
the system.
10
4
10
5
10
6
10
7
10
8
10
9
-140
-120
-100
-80
-60
-40
-20
0
spice
matlab
R. B. Staszewski, All Digital Frequency Synthesizer in Deep Submicron CMOS, New Jersey: John Wiley & Sons, Inc., 2006.
AMS Verification Simulation
15

16. Auxiliary Feedback Loop
• The injection signals are directly driven into the LC tank
where the interpolation takes place.
16
Buffer
Iinjejθ
DPR
a b
Iinj1
Iinj2
a·Iu
b·Iu
+
Iosc
DCO
+
Vosc
-
Vosc+
VI0
VI90
Phase
Generator
fo fo 3fo
VI0
VI90
Iinj1
Iinj2 fo
LC Tank
Injection
Current
Iinj θk
(a)
θ(a,b)
a·Iu b·Iu
3fo
τc
a·Iu
b·Iu
(a+b)·Iu
Vosc+ Vbuff+
(b)
Vbuff+
Iinj1 Iinj2+

17. Calibration of τc1
• τc1 is calibrated real time by applying small modulation with DPR over all
settings of τc1 and estimating KDCO for each setting.
• KDCO is estimated by monitoring samples of phase detector output ‘PHE’
while the IL oscillator is locked by the digital PLL.
• The optimum τc1 is where estimated KDCO is maximum.
(b)(a)
Vosc+
VI0
VI90
Vosc+
VI0
VI90
Vosc+
VI0
VI90
KDCOT
τc1,opt τc1
(1) (2)
(3) (4)
17

18. IC Micrograph
• Technology: TSMC 40nm 1P7M CMOS; Area: 420μm х 750μm
(Core), 1250μm x 1035μm (with pad frame), Pad Count: 32
18

19. Measurement Results
Step Size Ir = 0.15
19

20. Measurement Results
Step Size Ir = 0.75
20

21. Measurement Results
Step Size with ΣΔ Ir = 0.27
• Step Size with ΣΔ processing = 1.71MHz/2^6 ~ 24.8kHz
21

22. Measurement Results
Phase Noise Ir = 0.15
22
-150
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 1.E+08
PhaseNoise(dBc/Hz)
Offset Frequency (Hz)
DCO Free Running
θ=-45⁰
θ=+45⁰
fo=4.6GHz; Ir=0.15
PN@1MHz=-118dBc/Hz

23. Measurement Results
FM Range and Step Size vs. Ir
• By controlling Ir, the DUT can be reconfigured to support a
wide range of FM bandwidths.
23
1000
1200
1400
1600
1800
2000
2200
2400
90.00
100.00
110.00
120.00
130.00
140.00
150.00
160.00
170.00
180.00
190.00
200.00
210.00
0.3 0.4 0.5 0.6 0.7 0.8 0.9
StepSize(kHz/deg)
FMRange(MHz)
Ir=Iinj/Iosc

24. Measurement Results
Phase Noise vs. Ir
• Phase noise degrades considerably at high injection currents.
Far-out noise limited by divider / buffer circuit.
24
-112
-111
-110
-109
-108
-107
-106
-105
-104
1000 1200 1400 1600 1800 2000 2200 2400
1-MHzPhaseNoise(dBc/Hz)
Step Size (kHz/deg)

25. Measurement Results
τc1 Calibration
• Optimum τc1 = 2 Delays
25

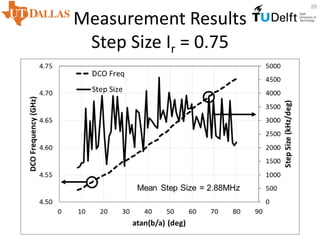
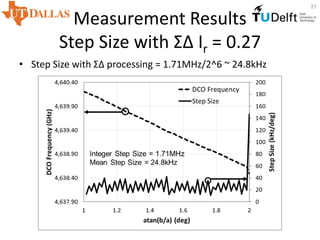
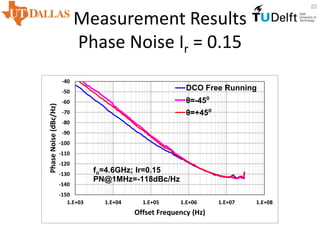
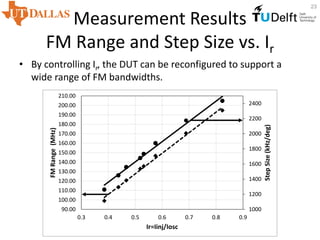
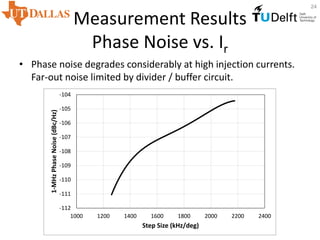
26. Measurement Results
Comparison Table
[2] [5] [4] [3]
65nm 65nm 65nm 90nm
1.25 1.2 1.2
3 2.5 8 3.3
Coarse (MHz) 780 140 600
Fine (MHz) 2-12(a)
NBM WBM
0.558(a)
200(a)
60 12
9(a)
2280(a)
0.15-1.5(a)
270 5
1MHz -118 -103 -127.5 -115.1 -118
20MHz -130(c)
-130(c)
-138
26.9 16.7 16 10 2
0.27 0.27 0.32 0.18 0.18
(a) Without ΣΔ dithering.
(b) All phase noise data at DCO output.
(c) Output buffer limited.
Injection Locked
Capacitive
Tuning
Capacitive
Tuning
Injection
Locked
Capacitive
Tuning
Tuning Range (Injection Locked) (MHz)
Fine Freq Resolution (kHz)
Phase noise (dBc/Hz)(b)
Current consumption (mA)
Oscillator core area (mm2
)
Oscillator description
Frequency (GHz) 4.6
Tuning Range (Capacitive) 2100
Mode
This Work
Technology 40nm
Supply Voltage (V) 1.1
26

27. References
• http://www.researchgate.net/profile/Imran_Bashir5
– “An SoC with Automatic Bias Calibration of an RF Oscillator ”
– “Mitigation of RF Oscillator Pulling through Adjustable Phase
Shifting”
• [1] C.-M. Hung, et. al, "A digitally controlled oscillator system for SAW-less
transmitters in cellular handsets," IEEE JSSC, vol. 41, no. 5, pp. 1160-1170,
May 2006.
• [2] L. Fanori, et. al, "Capacitive Degeneration in LC-Tank Oscillator for DCO
Fine-Frequency Tuning," IEEE JSSC, vol. 45, no. 12, pp. 2737-2745, 2010.
• [3] J. Zhuang et al., "A 3.3 GHz LC-based digitally controlled oscillator with 5
kHz frequency resolution," in Proc. IEEE ASSCC, 2007, pp. 428-431.
• [4] A. Visweswaran, et al., "Fine Frequency Tuning using Injection-Control in
a 1.2V 65nm CMOS Quadrature Oscillator," in IEEE RFIC, 2012.
• [5] K. Kodama, et. al, "A High Frequency Resolution Digitailly Controlled
Oscillator Using Single Period Switching Scheme," in ESSCC, Helsinki, 2011.
27