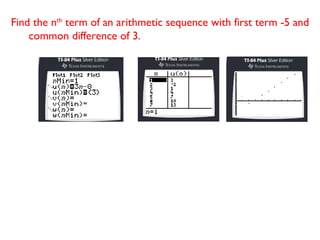
An arithmetic sequence is a sequence where the difference between consecutive terms is constant. The common difference (d) is this constant value. The recursive formula for an arithmetic sequence is Un = Un-1 + d and the explicit formula is Un = U1 + (n - 1)d. Given values for the first few terms, you can find the common difference and write the recursive and explicit formulas to generate all terms of the sequence.

1. Arithmetic Sequences

2. Section 1.3 Arithmetic Sequences
An arithmetic sequence is a sequence in which
the difference between each term and the
preceding term is always constant.
Which of the following sequences is arithmetic?
a. {14, 10, 6, 2, -2, -6, -10, . . . }
b. {3, 5, 8, 12, 17, . . . }
a. yes, the difference between each term is -4
b. no, the difference between the first two terms is 2
and the difference between the 2nd and 3rd term is 3.

3. Recursive Form of an Arithmetic
Sequence
Un = Un-1 + d
for some constant d and all n > 2
The number d is called the common difference of the
arithmetic sequence.

4. Graph of an Arithmetic Sequence
• If {Un} is an arithmetic sequence with U1 = 3
and U2 = 4.5 as its first two terms,
• a. Find the common difference.
• b. Write the sequence as a recursive
function.
• c. Give the first six terms of the sequence.
• d. Graph the sequence.

5. •
a. Find the common difference.
• U - U = 4.5 - 3 = 1.5
2 1
• The common difference is 1.5

6. • b. Write the sequence as a recursive function.
•U 1 = 3, Un = Un-1 + 1.5, for n > 2
First Method for Always one
Term finding nth term greater than
by using the subscript of first
preceding term. term.

7. • c. Give the first six terms of the
sequence.

8. Explicit Form of an Arithmetic Sequence
• In an arithmetic sequence {Un} with common
difference d, Un = U1 + (n - 1)d for every n > 1
Find the nth term of an arithmetic sequence with first term -5 and
common difference of 3. Sketch a graph of the sequence.
Un = U1 + (n - 1)d
= -5 + (n - 1)3
= -5 + 3n - 3
= 3n - 8

9. Find the nth term of an arithmetic sequence with first term -5 and
common difference of 3. Sketch a graph of the sequence.

10. Finding a Term of an Arithmetic
Sequence
What is the 45th term of the arithmetic sequence whose first
three terms are 5, 9, and 13?
First find d; d = 9 - 5 = 4
Second find explicit form: Un = 5 + (n - 1)4
Un = 4n + 1
Then find 45th term: U45 = 4(45) + 1
U45 = 181

11. Finding Explicit and Recursive
Formulas
If {Un} is an arithmetic sequence with U6 = 57 and
U10 = 93, find U1, a recursive formula, and an explicit
formula for Un.
To find d when given to non-consecutive terms use the formula:
d = Um --Un
m n
d = 93 -- 57
10 6
=9

12. Finding U1
Select either of the given terms and substitute
into Explicit formula. Un = U1 + (n - 1)d
U6 = 57 U10 = 93
57 = U1 + (6 - 1)9 93 = U1 + (10 - 1)9
U1 = 12 U1 = 12

13. FORMULAS
Explicit Form Recursive Form
Un = U1 + (n - 1)d Un = Un-1 + d
Un = 12 + (n - 1)9 Un = Un-1 + 9, for n > 2
Un = 9n + 3, for n > 1