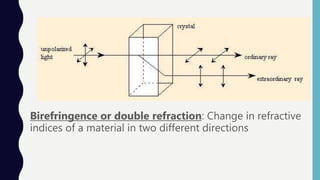
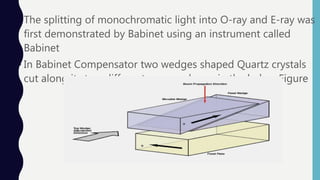
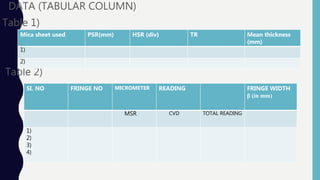
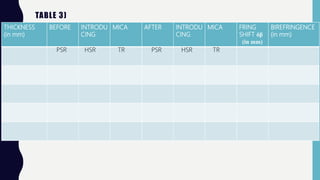
This document describes how to determine the birefringence of mica using a Babinet compensator. A Babinet compensator contains two quartz wedges that allow plane polarized light to split into ordinary and extraordinary rays when passed through a birefringent material. By measuring the fringe shift caused when mica is placed between the polarizer and compensator, and using the fringe width and material thickness in an equation, the birefringence of the mica can be calculated. The experiment involves setting up the apparatus, measuring the fringe width without mica, measuring the fringe shift caused when mica is added, and using these values in the equation (no-ne) = λδβ/βt

1. BIREFRINGENCE
OF MICA
USING A BABINET
COMPENSATOR

2. AIM: TO DETERMINE THE BIREFRINGENCE OF MICA USING A
BABINET COMPENSATOR
• Isotropic material: Light travels through a material in any direction
with same velocity
example: glass
• Anisotropic or Birefringent material: Light travels through a
material with two different velocities in two different directions(O-
ray & E- ray)
example: Quartz , Calcite
• Ordinary ray: The ray of light traveling along the optical axis with
its electric field perpendicular it is called ordinary-ray (O-ray)
• Extra-ordinary ray: The ray of light with its E-field parallel to optical
axis is called extra-ordinary ray (E-ray).

3. Birefringence or double refraction: Change in refractive
indices of a material in two different directions

4. Babinet compensator: Babinet compensator shown
in Figure-1 is an optical instrument designed by
Jacques Babinet (1794-1872) a French physicist

5. • The splitting of monochromatic light into O-ray and E-ray was
first demonstrated by Babinet using an instrument called
Babinet
• In Babinet Compensator two wedges shaped Quartz crystals
cut along its two different axes as shown in the below Figure

6. • On such a crystal monochromatic plane polarized light is
allowed to fall. The plane polarized light gets refracted and the
O-rays and E-rays that are produced interfere with each other
to form fringes. These fringes can be observed.
• The birefringent material is placed after the polarizer on which
first the plane polarized light is allowed to fall
• The O-rays and E-rays coming out of the material is allowed to
fall on Quartz crystal of the Babinet compensator. Inside the
compensator quartz crystal these rays further refract and hence
the original fringes get shifted
• By measuring the increase in fringe shift, birefringence of the
material placed between the polarizer and the compensator
can be estimated

7. Birefringence pattern

8. Velocity of light in a medium is defined as
V medium =c/n
Where
‘c’ is velocity of light in vacuum ‘n’ is refractive index of the
medium
Because of double refractive index the velocities of light in two
different directions are different. Hence velocity along optical axis
(X-axis)
V⊥= c/no
V// = c/ne
c = V// ne= V⊥ no
∆ = (no -ne )t

9. If this path difference is integral multiple of wavelength
∆ = nλ
The path difference due to second birefringent material is
∆= (λ/ β)δβ
FORMULA USED:
(no-ne) = λδβ/βt
Where
• δβ is the fringe shift with second material
• β is fringe width without the second material
• t is the thickness of the second material
• λ is wavelength of the light used
• (no-ne) is difference in the refractive indices of the O and E rays.

10. • EXPERIMENTAL SETUP (PICTURES )

11. PROCEDURE
• Set up the apparatus
• Using the micrometer of the Babinet compensator, the
fringe width is measured
• mica sheets is introduced between the polarizer and
compensator so there will be fringe shift
• Measure the fringe shift through micrometer
• The experiment is repeated for different fringes and
time the fringe shift is calculated and calculate the
birefringence by using the formula.

12. • DATA (TABULAR COLUMN)
Table 1)
Table 2)
Mica sheet used PSR(mm) HSR (div) TR Mean thickness
(mm)
1)
2)
SI. NO FRINGE NO MICROMETER READING FRINGE WIDTH
β (in mm)
MSR CVD TOTAL READING
1)
2)
3)
4)

13. TABLE 3)
THICKNESS
(in mm)
BEFORE INTRODU
CING
MICA AFTER INTRODU
CING
MICA FRING
SHIFT δβ
(in mm)
BIREFRINGENCE
(in mm)
PSR HSR TR PSR HSR TR

14. FORMULA USED:
(no-ne) = λδβ/βt
Where
• δβ is the fringe shift with second material
• β is fringe width without the second material
• t is the thickness of the second material
• λ is wavelength of the light used
• (no-ne) is difference in the refractive indices of the O and
E rays.

15. • RESULT:
• BIFRINGENCE OF MICA IS FOUND TO BE =

16. THANK YOU