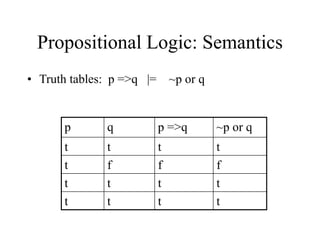
Propositional logic allows reasoning about statements that are either true or false. It has applications in knowledge representation and automated reasoning. Key concepts include: - Representing knowledge as logical propositions connected by operators like "and", "or", and "implies". - Using semantics based on truth tables and possible worlds to define logical entailment between statements. - Performing inference through syntactic rules like resolution to derive new true statements from existing ones in a sound and complete manner. - Translating natural language statements and rules of inference into propositional logic for automated reasoning. However, propositional logic has limitations in what can be represented, including quantification, relations, probabilities, and uncertainty. More

1. Propositional Logic
or how to reason correctly
Chapter 8 (new edition)
Chapter 7 (old edition)

2. Goals
• Feigenbaum: In the knowledge lies the
power. Success with expert systems. 70’s.
• What can we represent?
– Logic(s): Prolog
– Mathematical knowledge: mathematica
– Common Sense Knowledge: Lenat’s Cyc has a
million statement in various knowledge
– Probabilistic Knowledge: Bayesian networks
• Reasoning: via search

3. History
• 300 BC Aristotle: Syllogisms
• Late 1600’s Leibnitz’s goal: mechanization
of inference
• 1847 Boole: Mathematical Analysis of
Logic
• 1879: Complete Propositional Logic: Frege
• 1965: Resolution Complete (Robinson)
• 1971: Cook: satisfiability NP-complete
• 1992: GSAT Selman min-conflicts

4. Syllogisms
• Proposition = Statement that may be either
true or false.
• John is in the classroom.
• Mary is enrolled in 270A.
• If A is true, and A implies B, then B is true.
• If some A are B, and some B are C, then
some A are C.
• If some women are students, and some
students are men, then ….

5. Concerns
• What does it mean to say a statement is
true?
• What are sound rules for reasoning
• What can we represent in propositional
logic?
• What is the efficiency?
• Can we guarantee to infer all true
statements?

6. Semantics
• Model = possible world
• x+y = 4 is true in the world x=3, y=1.
• x+y = 4 is false in the world x=3, y = 1.
• Entailment S1,S2,..Sn |= S means in every
world where S1…Sn are true, S is true.
• Careful: No mention of proof – just
checking all the worlds.
• Some cognitive scientists argue that this is
the way people reason.

7. Reasoning or Inference Systems
• Proof is a syntactic property.
• Rules for deriving new sentences from old
ones.
• Sound: any derived sentence is true.
• Complete: any true sentence is derivable.
• NOTE: Logical Inference is monotonic.
Can’t change your mind.

8. Proposition Logic: Syntax
• See text for complete rules
• Atomic Sentence: true, false, variable
• Complex Sentence: connective applied to
atomic or complex sentence.
• Connectives: not, and, or, implies,
equivalence, etc.
• Defined by tables.

9. Propositional Logic: Semantics
• Truth tables: p =>q |= ~p or q
p q p =>q ~p or q
t t t t
t f f f
t t t t
t t t t

10. Implies =>
• If 2+2 = 5 then monkeys are cows. TRUE
• If 2+2 = 5 then cows are animals. TRUE
• Indicates a difference with natural
reasoning. Single incorrect or false belief
will destroy reasoning. No weight of
evidence.

11. Inference
• Does s1,..sk entail s?
• Say variables (symbols) v1…vn.
• Check all 2^n possible worlds.
• In each world, check if s1..sk is true, that s
is true.
• Approximately O(2^n).
• Complete: possible worlds finite for
propositional logic, unlike for arithmetic.

12. Translation into Propositional Logic
• If it rains, then the game will be cancelled.
• If the game is cancelled, then we clean house.
• Can we conclude?
– If it rains, then we clean house.
• p = it rains, q = game cancelled r = we clean
house.
• If p then q. not p or q
• If q then r. not q or r
• if p then r. not p or r (resolution)

13. Concepts
• Equivalence: two sentences are equivalent
if they are true in same models.
• Validity: a sentence is valid if it true in all
models. (tautology) e.g. P or not P.
– Sign: Members or not Members only.
– Berra: It’s not over till its over.
• Satisfiability: a sentence is satisfied if it true
in some model.

14. Validity != Provability
• Goldbach’s conjecture: Every even number
(>2) is the sum of 2 primes.
• This is either valid or not.
• It may not be provable.
• Godel: No axiomization of arithmetic will
be complete, i.e. always valid statements
that are not provable.

15. Natural Inference Rules
• Modus Ponens: p, p=>q |-- q.
– Sound
• Resolution example (sound)
– p or q, not p or r |-- q or r
• Abduction (unsound, but common)
– q, p=>q |-- p
– ground wet, rained => ground wet |-- rained
– medical diagnosis

16. Natural Inference Systems
• Typically have dozen of rules.
• Difficult for people to use.
• Expensive for computation.
– e.g. a |-- a or b
– a and b |-- a
• All known systems take exponential time in
worse case. (co-np complete)

17. Full Propositional Resolution
• clause 1: x1 +x2+..xn+y (+ = or)
• clause 2: -y + z1 + z2 +… zm
• clauses contain complementary literals.
• x1 +.. xn +z1 +… zm
• y and not y are complementary literals.
• Theorem: If s1,…sn |= s then
s1,…sn |-- s by resolution.
Refutation Completeness.
Factoring: (simplifying: x or x goes to x)

18. Conjunctive Normal Form
• To apply resolution we need to write what
we know as a conjunct of disjuncts.
• Pg 215 contains the rules for doing this
transformation.
• Basically you remove all  and => and
move “not’s” inwards. Then you may need
to apply distributive laws.

19. Proposition -> CNF
Goal: Proving R
• P
• (P&Q) =>R
• (S or T) => Q
• T
• Distributive laws:
• (-s&-t) or q
(-s or q)&(-t or q).
• P
• -P or –Q or R
• -S or Q
• -T or Q
• T
• Remember:implicit
adding.

20. Resolution Proof
• P (1)
• -P or –Q or R (2)
• -S or Q (3)
• -T or Q (4)
• T (5)
• ~R (6)
• -P or –Q : 7 by 2 & 6
• -Q : 8 by 7 & 1.
• -T : 9 by 8 & 4
• empty: by 9 and 5.
• Done: order only
effects efficiency.

21. Resolution Algorithm
To prove s1, s2..sn |-- s
1. Put s1,s2,..sn & not s into cnf.
2. Resolve any 2 clauses that have
complementary literals
3. If you get empty, done
4. Continue until set of clauses doesn’t grow.
Search can be expensive (exponential).

22. Forward and Backward Reasoning
• Horn clause has at most 1 positive literal.
– Prolog only allows Horn clauses.
– if a, b, c then d => not a or not b or not c or d
– Prolog writes this:
• d :- a, b, c.
– Prolog thinks: to prove d, set up subgoals a, b,c
and prove/verify each subgoal.

23. Forward Reasoning
• From facts to conclusions
• Given s1: p, s2: q, s3: p&q=>r
• Rewrite in clausal form: s3 = (-p+-q+r)
• s1 resolve with s3 = -q+r (s4)
• s2 resolve with s4 = r
• Generally used for processing sensory
information.

24. Backwards Reasoning:
what prolog does
• From Negative of Goal to data
• Given s1: p, s2: q, s3: p&q=>r
• Goal: s4 = r
• Rewrite in clausal form: s3 = (-p+-q+r)
• Resolve s4 with s3 = -p +-q (s5)
• Resolve s5 with s2 = -p (s6)
• Resolve s6 with s1 = empty. Eureka r is true.

25. Davis-Putnam Algorithm
• Effective, complete propositional algorithm
• Basically: recursive backtracking with tricks.
– early termination: short circuit evaluation
– pure symbol: variable is always + or – (eliminate the
containing clauses)
– one literal clauses: one undefined variable, really
special cases of MRV
• Propositional satisfication is a special case of
Constraint satisfication.

26. WalkSat
• Heuristic algorithm, like min-conflicts
• Randomly assign values (t/f)
• For a while do
– randomly select a clause
– with probability p, flip a random variable in
clause
– else flip a variable which maximizes number of
satisfied clauses.
• Of course, variations exists.

27. Hard Satisfiability Problems
• Critical point: ratio of clauses/variables =
4.24 (empirical).
• If above, problems usually unsatsifiable.
• If below, problems usually satisfiable.
• Theorem: Critical range is bounded by
[3.0003, 4.598].

28. What can’t we say?
• Quantification: every student has a father.
• Relations: If X is married to Y, then Y is
married to X.
• Probability: There is an 80% chance of rain.
• Combine Evidence: This car is better than
that one because…
• Uncertainty: Maybe John is playing golf.