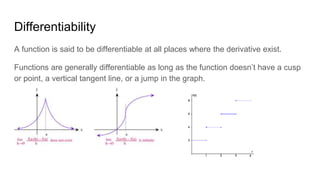
The document summarizes key topics in calculus including continuity, differentiability, and major theorems. It defines continuity as a function being defined, having a limit at a point, and the limit equaling the function value. Differentiability requires the derivative to exist. The Mean Value Theorem, Intermediate Value Theorem, and Extreme Value Theorem are stated as applying to continuous functions on closed intervals. Examples are provided for illustration but no solutions are shown. The presentation concludes by announcing upcoming review sessions on additional calculus topics.

1. Review Session
Continuity, Differentiability and Major Theorems

2. Topic 1
Continuity

3. Definitions
A function f is said to be continuous at x = c provided the following conditions are
satisfied:
1. f(c) is defined
2. The limit as x approaches c for f(x) exist
3. The limit form #2 and the the value from #1 are the same

4. Common areas
were functions are
not continuous
Holes
Vertical Asymptotes
Jumps in graphs

5. Topic 2
Differentiability

6. Differentiability
A function is said to be differentiable at all places where the derivative exist.
Functions are generally differentiable as long as the function doesn’t have a cusp
or point, a vertical tangent line, or a jump in the graph.

7. Topic 3
Mean Value Theorem

8. Mean Value Theorem, MVT
If f is continuous on the closed interval [a, b] and differentiable on the open interval
(a, b), then there exist a number c in (a, b) such that:

9. Topic 4
Intermediate Value Theorem

10. Intermediate Value Theorem, IVT
If f is continuous on the closed interval [a, b] and w is any number between f(a)
and f(b), then there is at least one number c in [a, b] such that f(c) = k
The IVT is often used to show that there must be an x-intercept on an interval

11. Topic 5
Extreme Value Theorem

12. Extreme Value Theorem
If f is continuous on a closed interval [a, b] then f has both a minimum and a
maximum on the interval

13. Example

14. Answer

15. Example

16. Answer

17. Example

18. Answer

19. Example

20. Example

21. Example

22. Answer

23. Example

24. Answer

25. Example

26. Answer

27. Example

28. Answer

29. Example

30. Answer

31. Example

32. Example

33. Review Session
Free Response

34. Example

35. Example Scoring Guide

36. Example

37. Example Scoring Guide

38. Example

39. Example Scoring Guide

40. Thank you for attending
I hope that this presentation has been helpful.
Don’t forget about the upcoming sessions:
BC only, this Thursday 3/30 at 7 PM on Polar
AB/BC combined next Tuesday 4/4 at 7 PM on Applications of Derivatives
https://docs.google.com/a/ncpublicschools.gov/forms/d/e/1FAIpQLSdPqmIGa0ctT
6IaPViMmuKk4GhLiahri7S75eQqLWr16_x0JA/viewform?c=0&w=1