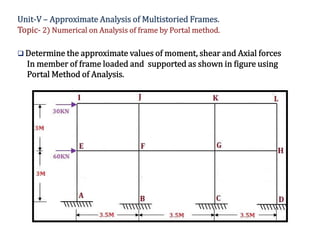
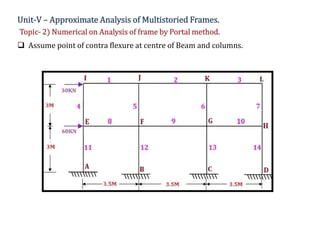
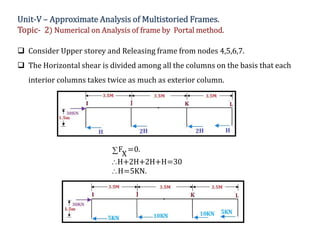
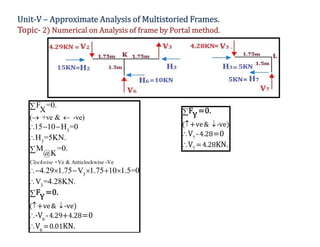
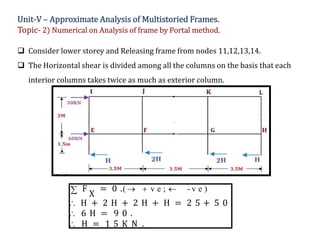
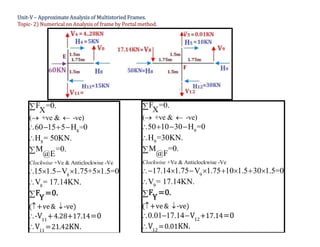
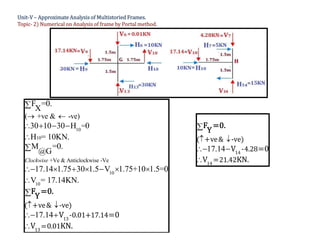
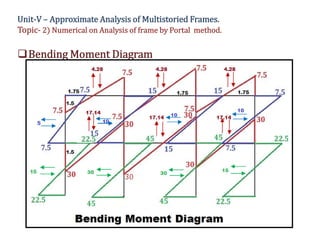
The document discusses numerical analysis for multistoried frames using the portal method in civil engineering, specifically as part of a course at Sanjivani College of Engineering. It includes calculations for determining the moment, shear, and axial forces in frame members, taking into account the distribution of horizontal shear between interior and exterior columns. Several numerical examples and calculations illustrate the application of the method.