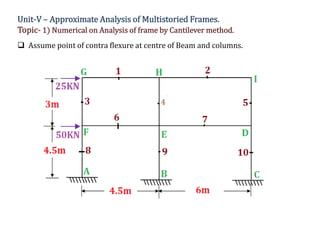
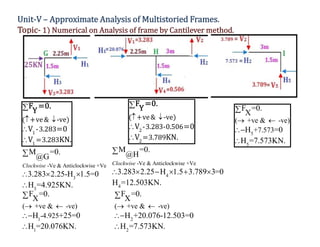
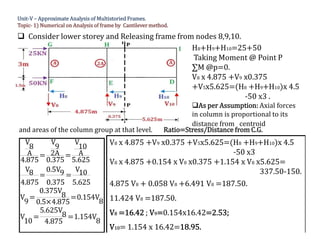
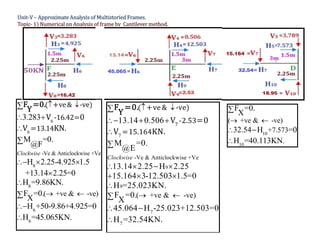
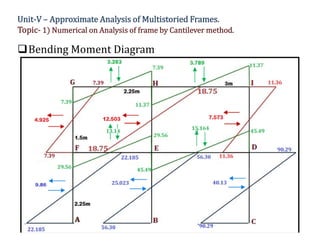
The document discusses advanced analysis of structures, specifically focusing on numerical calculations for multistoried frames using the cantilever method. It provides detailed steps to determine moments, shear, and axial forces in frame members, including calculations for centroid location and the effects of loading conditions. The analysis includes a series of equations and assumptions to derive the necessary structural values for a given frame configuration.

1. Sanjivani Rural Education Society's
Sanjivani College of Engineering, Kopargaon 423603.
Department of Civil Engineering
Course Title –Advance Analysis of Structures
T. Y.BTech Civil, Semester –II(CE313)
Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method
Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method
By,
Prof. Santosh. R. Nawale
(Assistant Professor)

2. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
 Determine the approximate values of moment, shear and Axial forces
In member of frame loaded and supported as shown in figure using
Cantilever Method of Analysis. Area of each exterior columns is one
half of the area of the Interior Columns.

3. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
 Assume point of contra flexure at centre of Beam and columns.

4. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
1) Determination of the CG of the Frame:
 Exterior Column= A; Interior Column=2A.
 To find out CG of the frame. Taking moment of the area of columns at leftmost
column axis.
 A1 x 0+A2 x 4.5+A3 x 10.5=(A1+A2+A3)
2A x4.5 +A x10.5=(A+2A+A)
19.5A=4A ; =4.875m.
X
X
A1 x 0+A2 x 4.5+A3 x 10.5=(A1+A2+A3)
2A x4.5 +A x10.5=(A+2A+A)
19.5A=4A ; =4.875m.
 Consider Upper storey and Releasing frame from nodes 3,4,5.
X
X X

5. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
H3+H4+H5=25
Taking Moment @ Point P
∑M @p=0.
V3 x 4.875 +V4 x0.375
+V5x5.625=(H3 +H4 +H5)x1.5.
As per Assumption: Axial forces in column is proportional to its distance from
centroid and areas of the column group at that level.
Ratio=Stress/Distance from C.G.
As per Assumption: Axial forces in column is proportional to its distance from
centroid and areas of the column group at that level.
Ratio=Stress/Distance from C.G.
V
V V
3 5
4
A 2A A
= =
4.875 0.375 5.625
V
V V
3 5
4
= =
4.875 0.375 5.625
0.375V
3
V = =0.154V
4 3
0.5×4.875
5.625V
3
V = =1.154V
3
5 4.875
V3 x 4.875 +V4 x0.375 +V5x5.625=(H3 +H4+H5)x1.5.
V3 x 4.875 +0.154 x V3 x0.375 +1.154 x V3 x5.625=
25x1.5.
4.875 V3 + 0.058 V3 +6.491 V3 =37.5
11.424 V3 =37.5.
V3 =3.283 ; V4=0.506 ;V5=3.789.

6. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
 


F =0.
Y
1
( +ve& -ve)
-3.283
=3.283
V =0
V KN.
 


F =0.
Y
2
( +ve& -ve)
-3.283-0.506
=3.789
V =0
V KN.
( +ve & -ve)
F =0.
X
 



F =0.
Y
1
1
( +ve& -ve)
-3.283
=3.283
V =0
V KN.


F =0.
Y
2
2
( +ve& -ve)
-3.283-0.506
=3.789
V =0
V KN.
5
5
( +ve & -ve)
+7.573
H =0
H =7.573KN.
 


3
3
-Ve & Anticlockwise +Ve
M =0.
@G
3.283 2.25-H 1.5=0
H =4.925KN.
Clockwise

  

1
1
( +ve & -ve)
-4.925
F =0.
X
H +25=0
H =20.076KN.
 



4
4
-Ve & Anticlockwise +Ve
M =0.
@H
3.283 2.25 H 1.5 3.789 3=0
H =12.503KN.
Clockwise

     
2
2
( +ve & -ve)
F =0.
X
H +20.076-12.503=0
H =7.573KN.
 




7. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
 Consider lower storey and Releasing frame from nodes 8,9,10.
H8+H9+H10=25+50
Taking Moment @ Point P
∑M @p=0.
V8 x 4.875 +V9 x0.375
+V5x5.625=(H8 +H9+H10)x 4.5
-50 x3 .
As per Assumption: Axial forces
in column is proportional to its
distance from centroid
and areas of the column group at that level. Ratio=Stress/Distance from C.G.
As per Assumption: Axial forces
in column is proportional to its
distance from centroid
and areas of the column group at that level. Ratio=Stress/Distance from C.G.
V V V
8 9 10
A 2A A
= =
4.875 0.375 5.625
V 0.5V V
8 9 10
= =
4.875 0.375 5.625
0.375V
8
V = =0.154V
9 8
0.5×4.875
5.625V
8
V = =1.154V
10 8
4.875
V8 x 4.875 +V9 x0.375 +V5x5.625=(H8 +H9+H10)x 4.5
-50 x3
V8 x 4.875 +0.154 x V8 x0.375 +1.154 x V8 x5.625=
337.50-150.
4.875 V8 + 0.058 V8 +6.491 V8 =187.50.
11.424 V8 =187.50.
V8 =16.42 ; V9=0.154x16.42=2.53;
V10= 1.154 x 16.42=18.95.

8. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.

9. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
6
3.283
 

 

F =0.
Y
( +ve& -ve)
-16.42=
=13.14
V 0
V KN.
13.14 0.506
 

  
F =0.
Y
7
( +ve& -ve)
-2.53
=15.164
V =0
V KN.
( +ve & -ve)
F =0.
X
 

6
6
8
8
6
6
-Ve & Anticlockwise +Ve
( +ve & -ve)
M =0.
@F
H 2.25-4.925 1.5
+13.14 2.25=0
H =9.86KN.
F =0.
X
H +50-9.86+4.925=0
H =45.065KN.
Clockwise
 


  





F =0.
Y
( +ve& -ve)
-16.42=
=13.14
V 0
V KN.
7
9
9
7
-Ve & Anticlockwise +Ve
( +ve & -ve)
13.14 0.506
M =0.
@E
13.14 2.25 H 2.25
15.164 3-12.503 1.5=0
H =25.023KN.
F =0.
X
45.064 H -25.023+12.503=0
Clockwise
 
  


   
  


 

F =0.
Y
7
( +ve& -ve)
-2.53
=15.164
V =0
V KN.
7
H =32.54KN.
10
10
( +ve & -ve)
+7.573
32.54 H =0
H =40.113KN.
 
 


10. Unit-V – Approximate Analysis of Multistoried Frames.
Topic- 1) Numerical on Analysis of frame by Cantilever method.
Bending Moment Diagram

11. THANK YOU