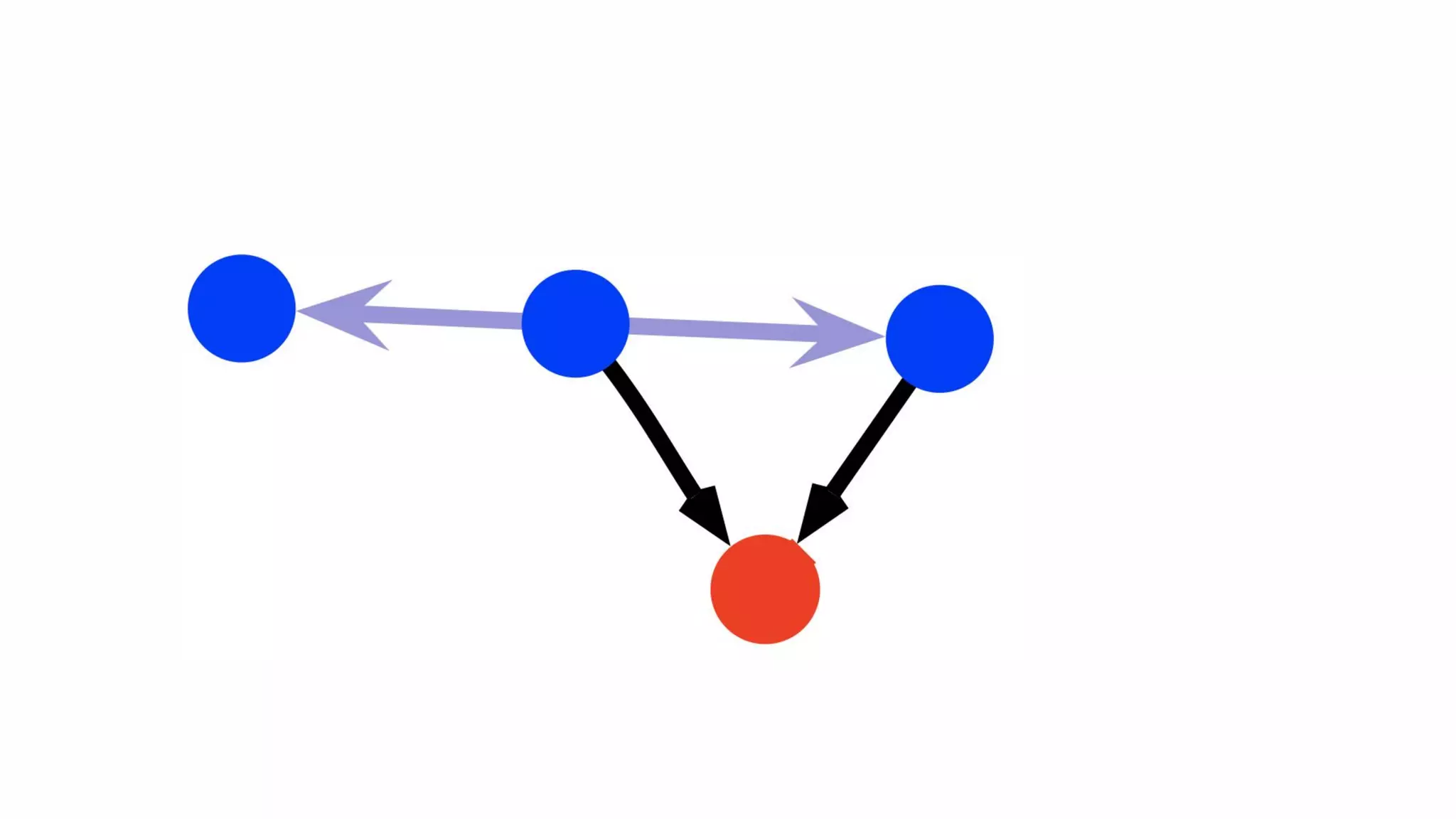
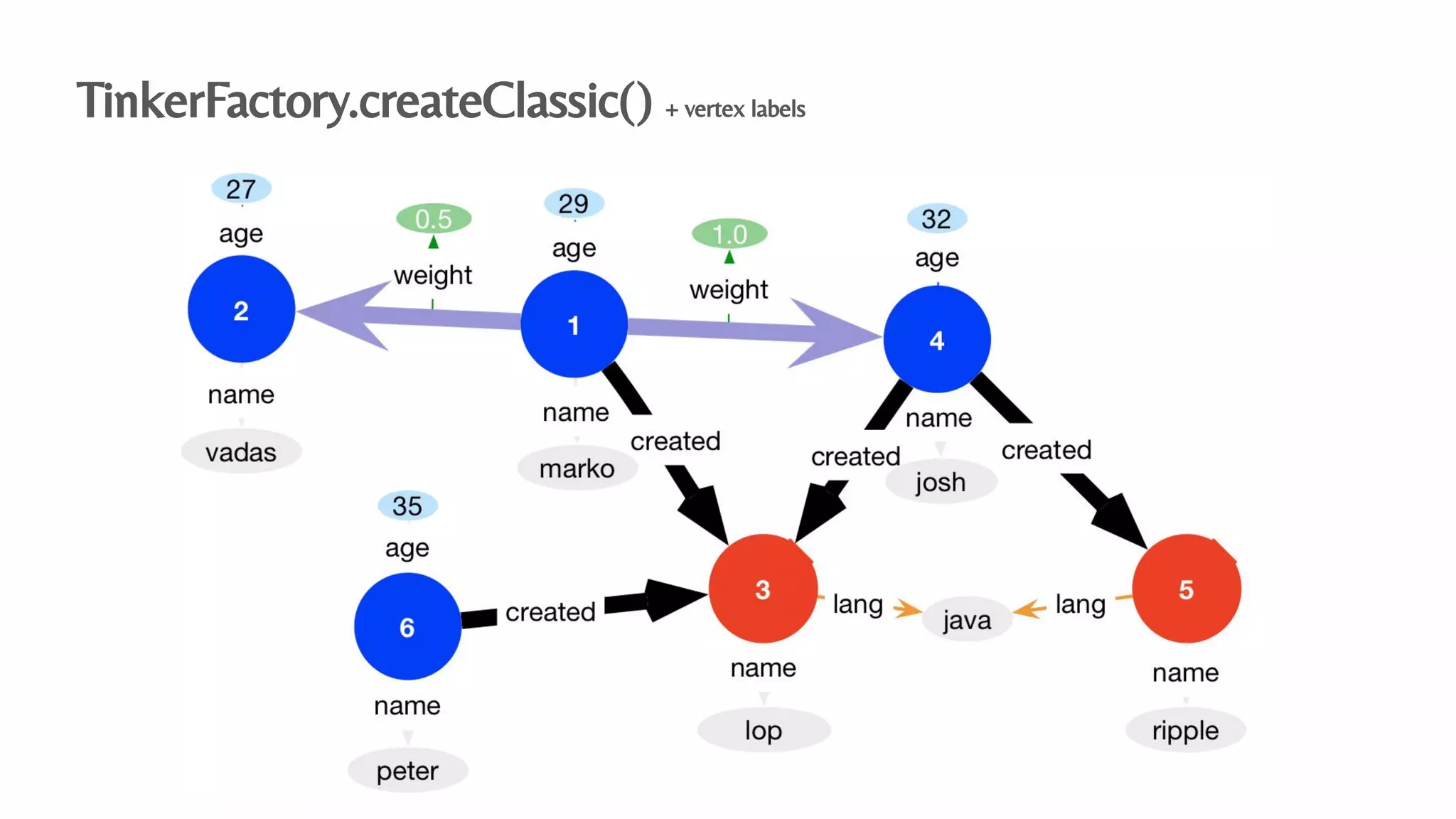
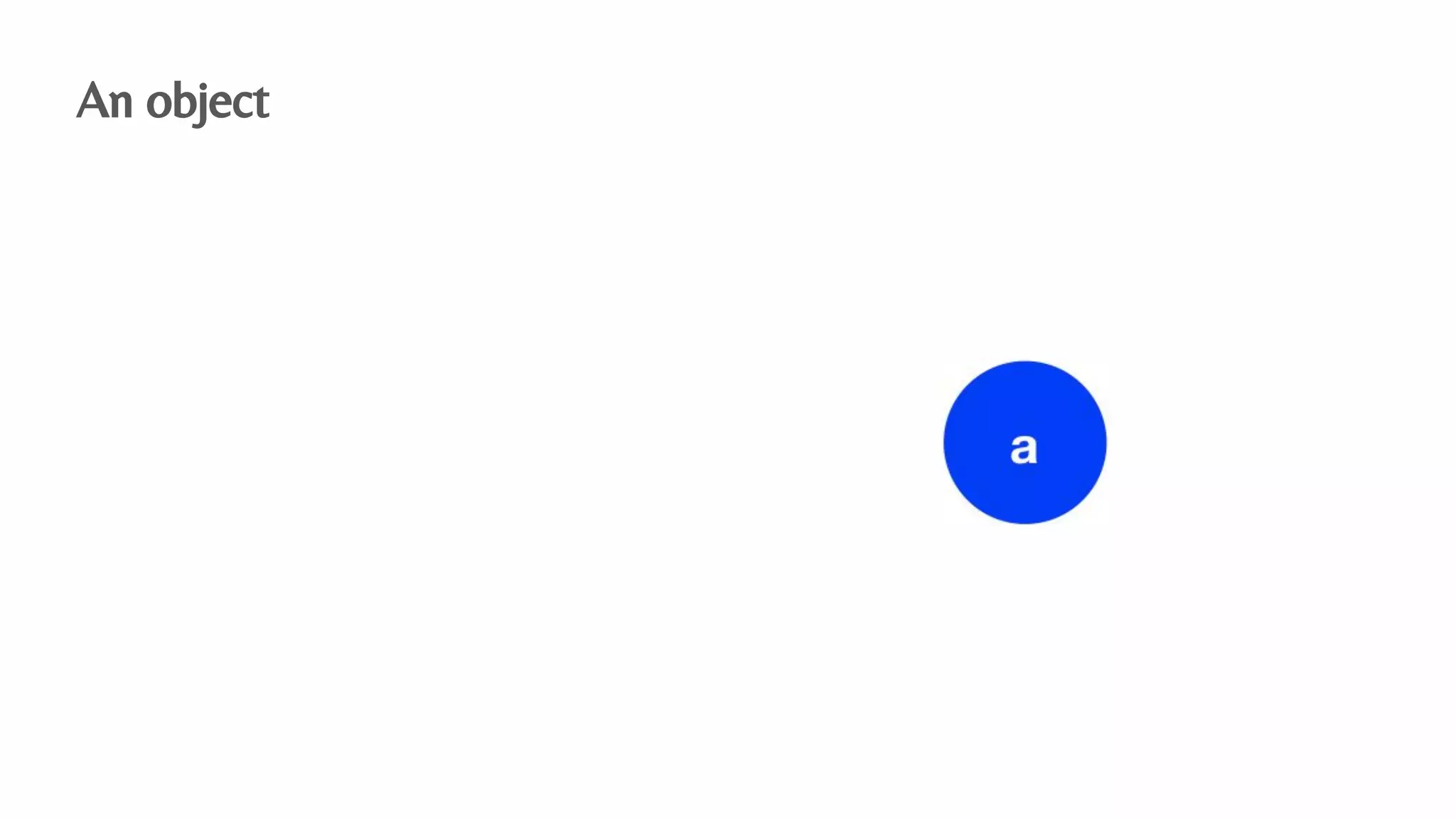
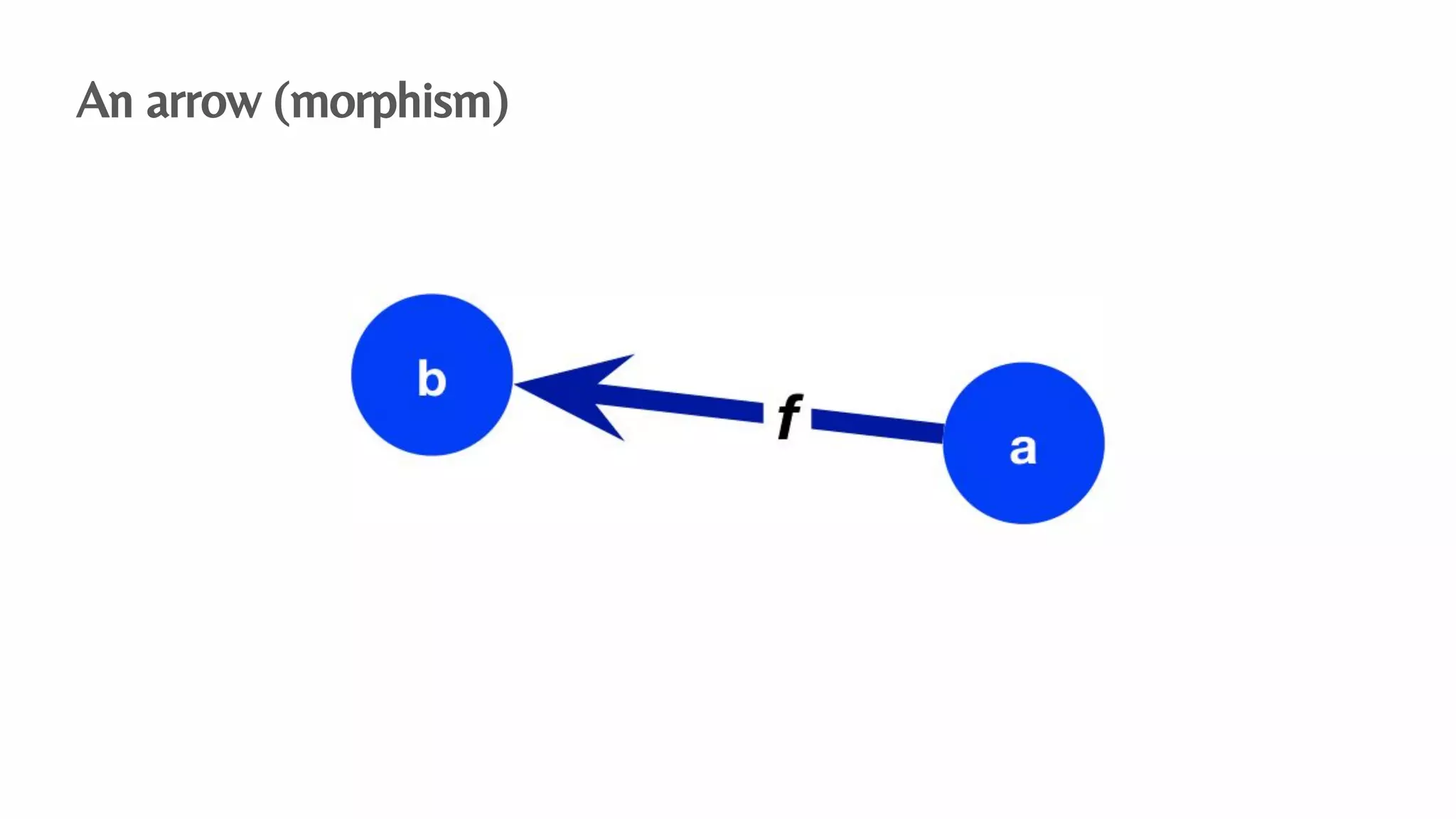
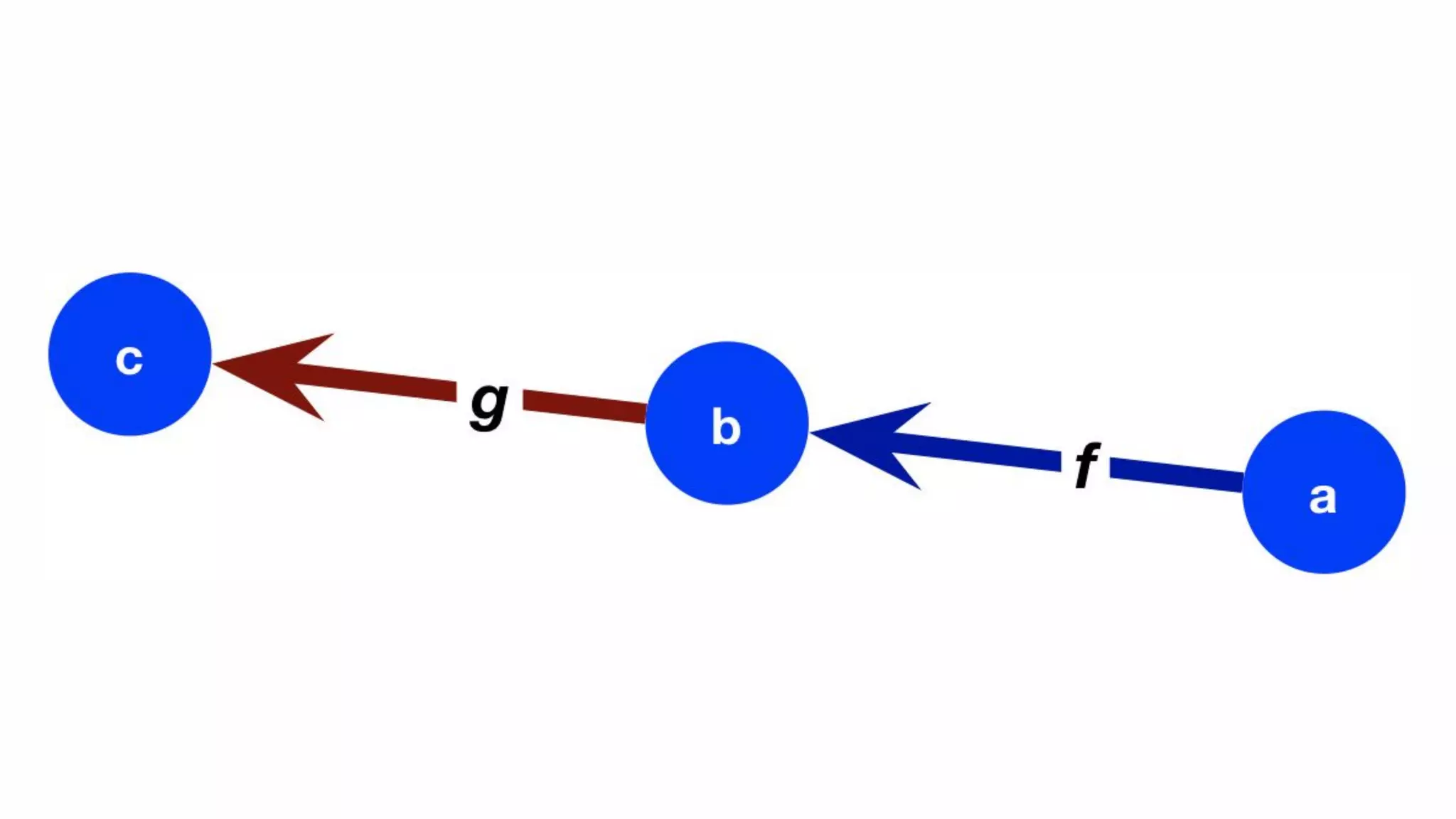
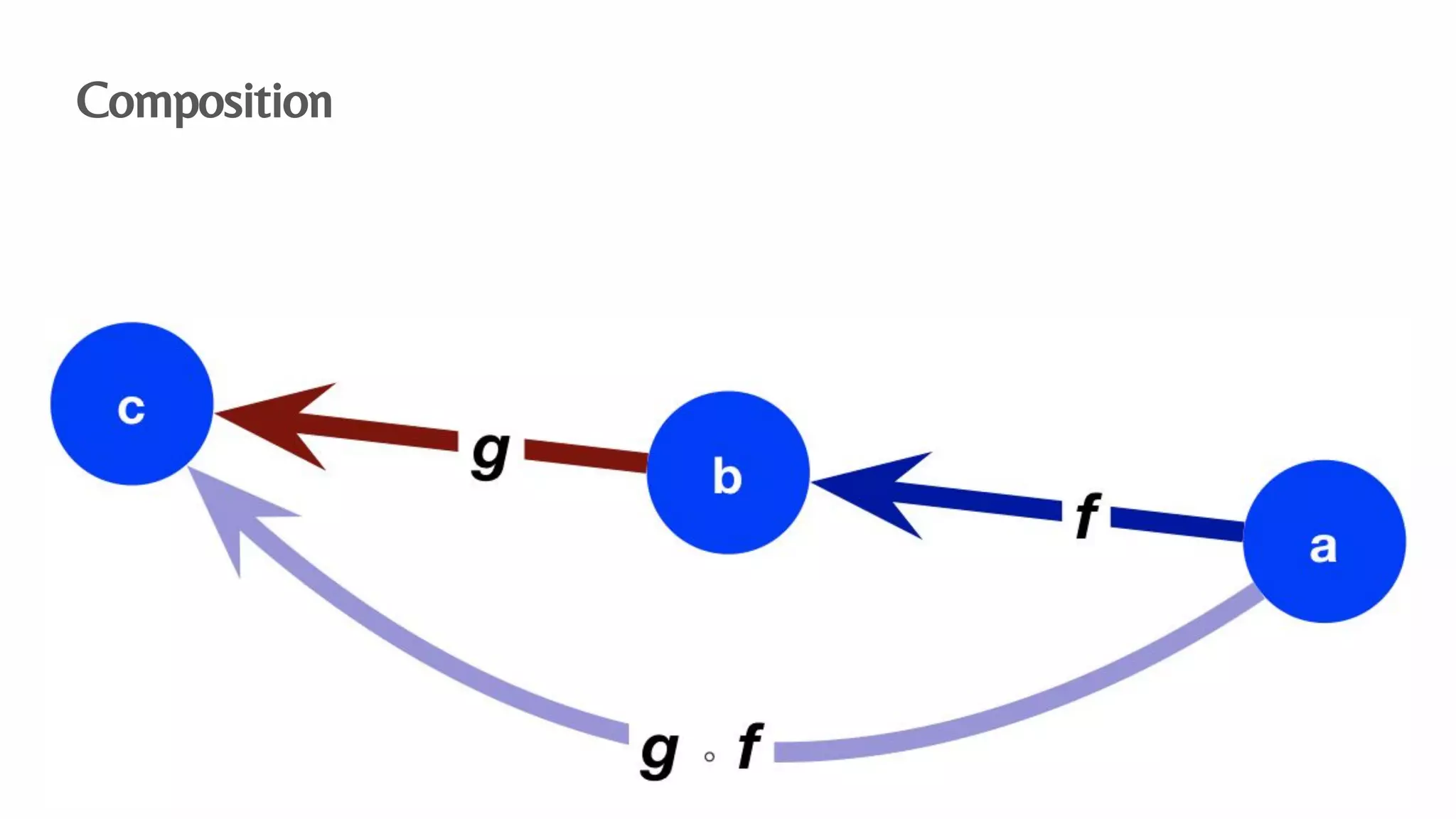
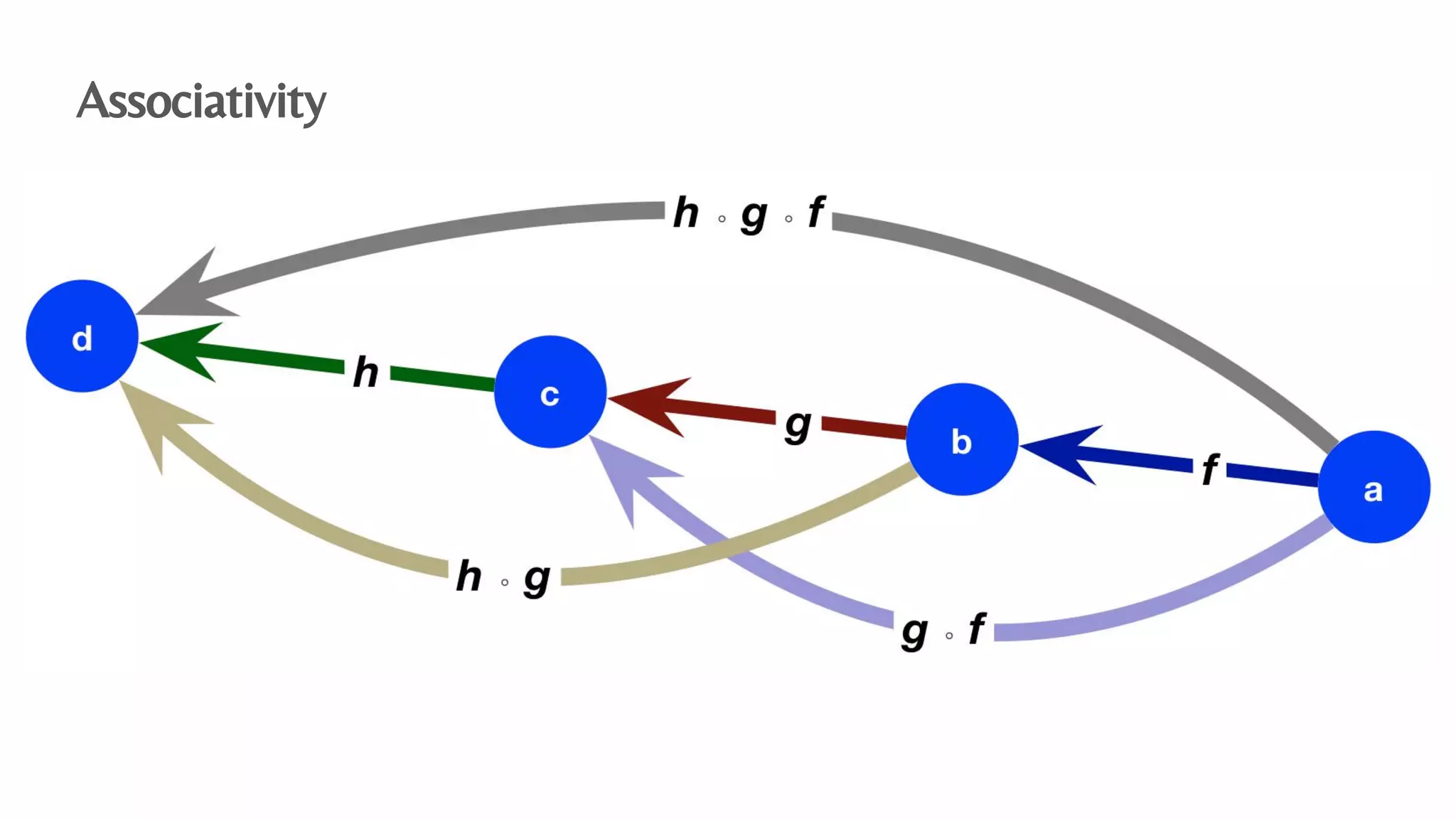
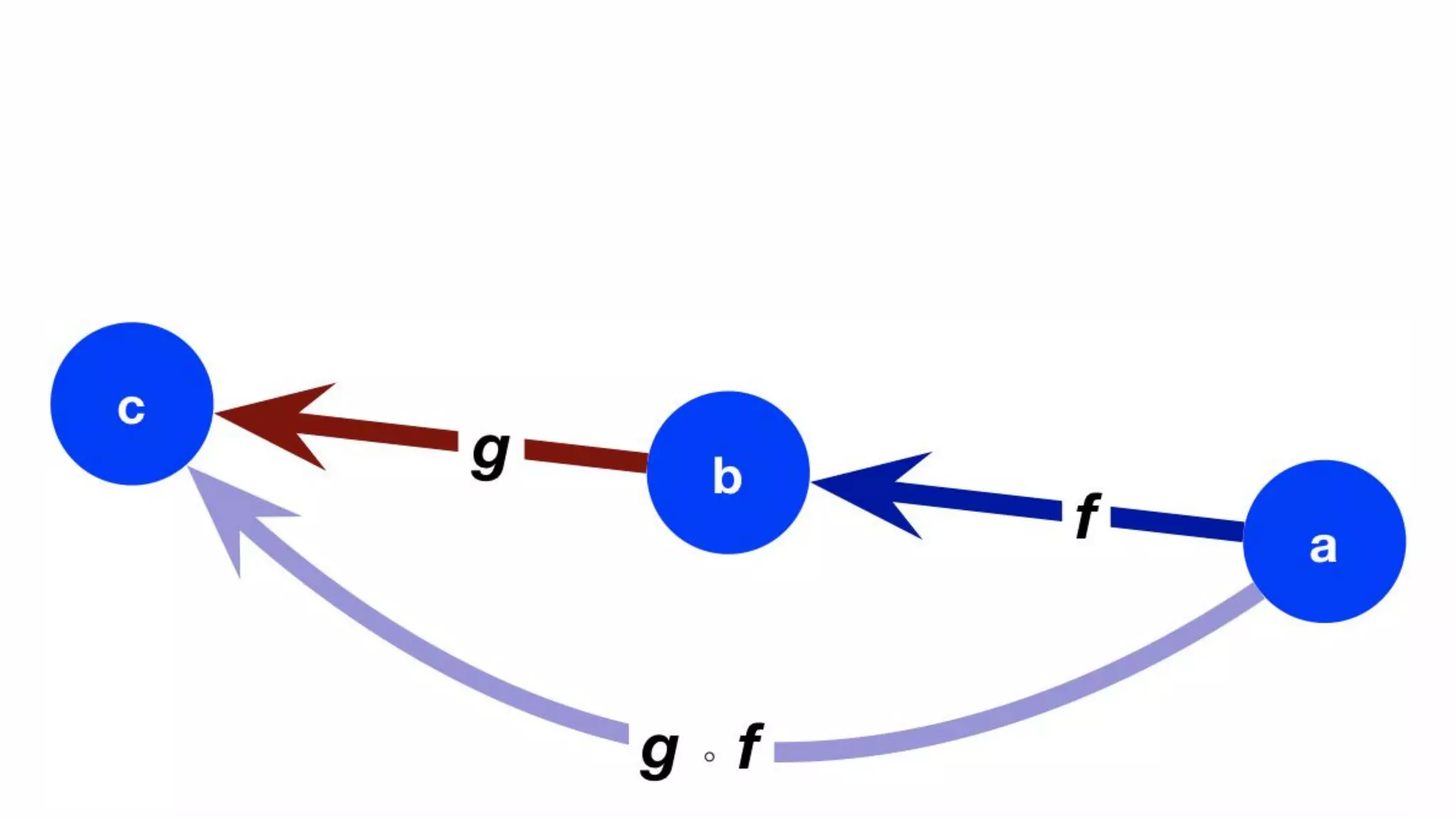
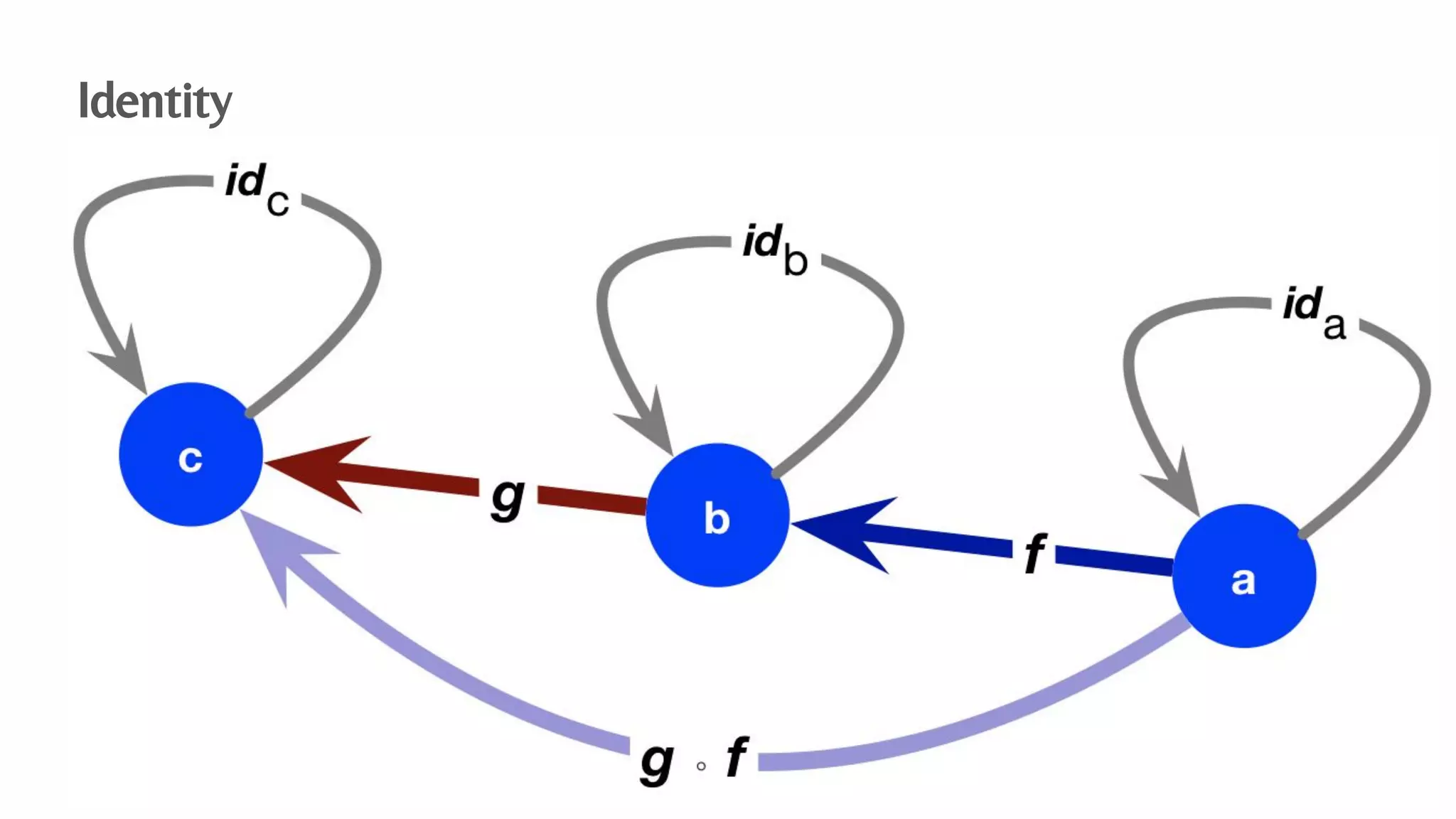
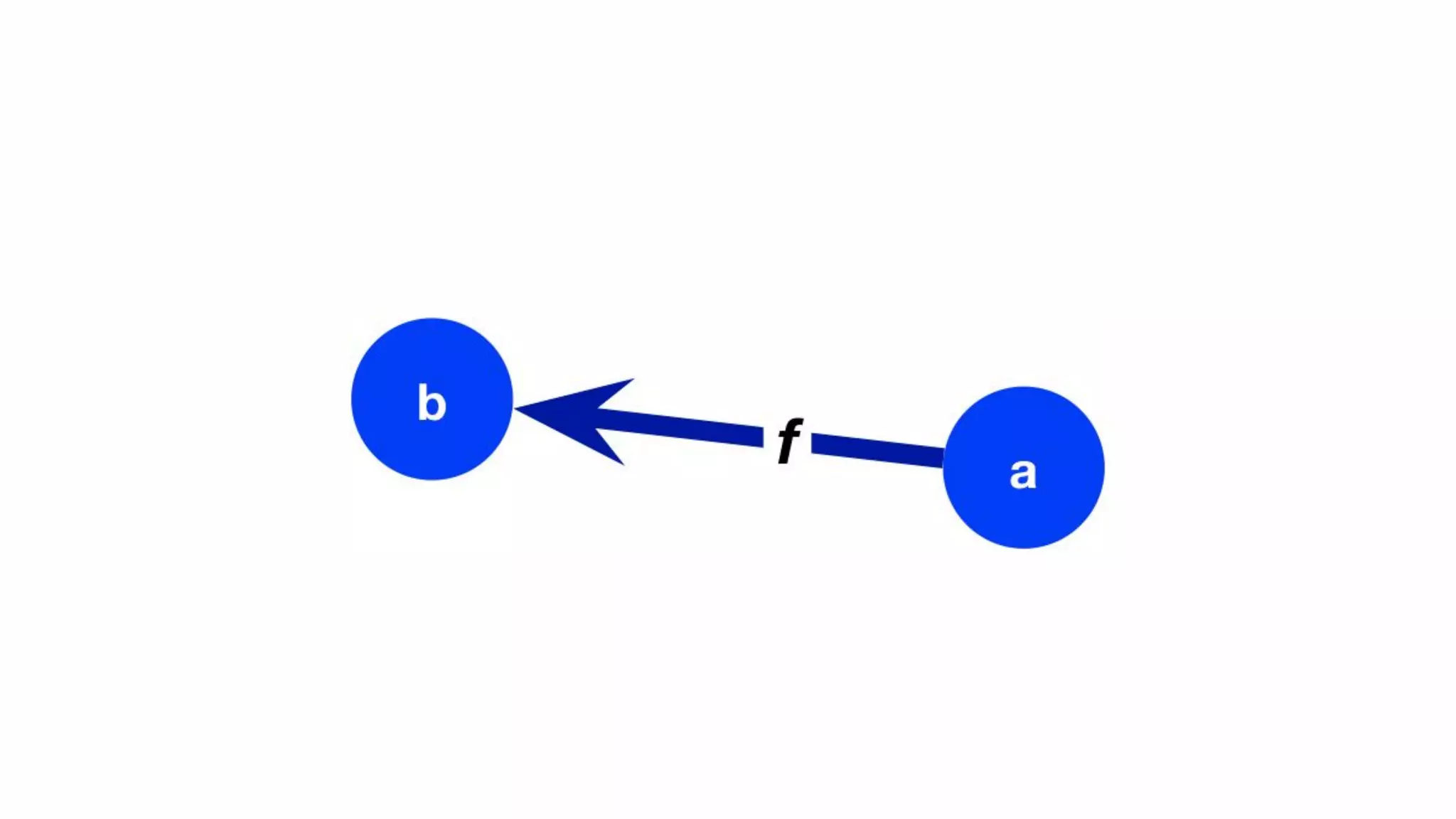
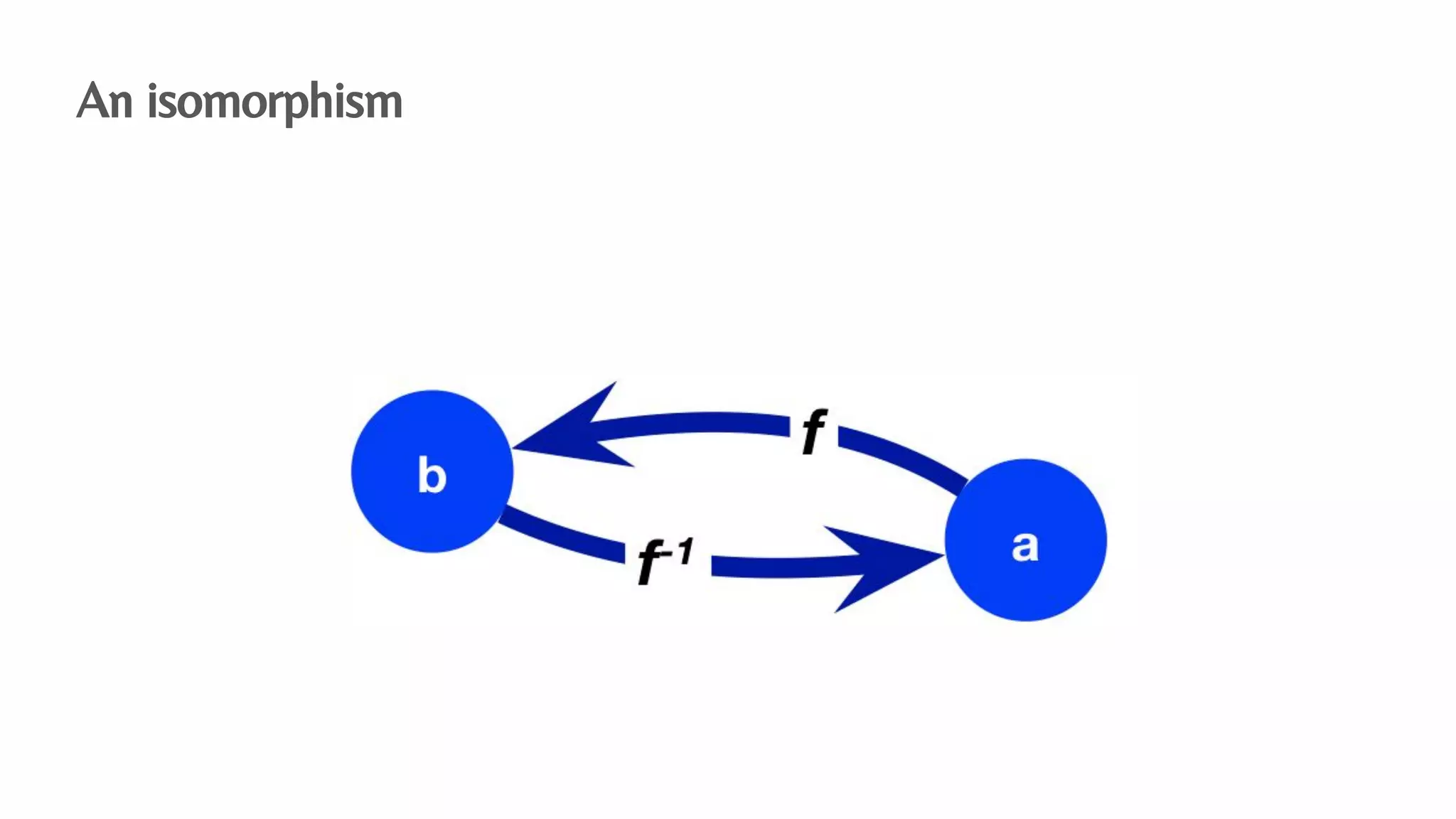
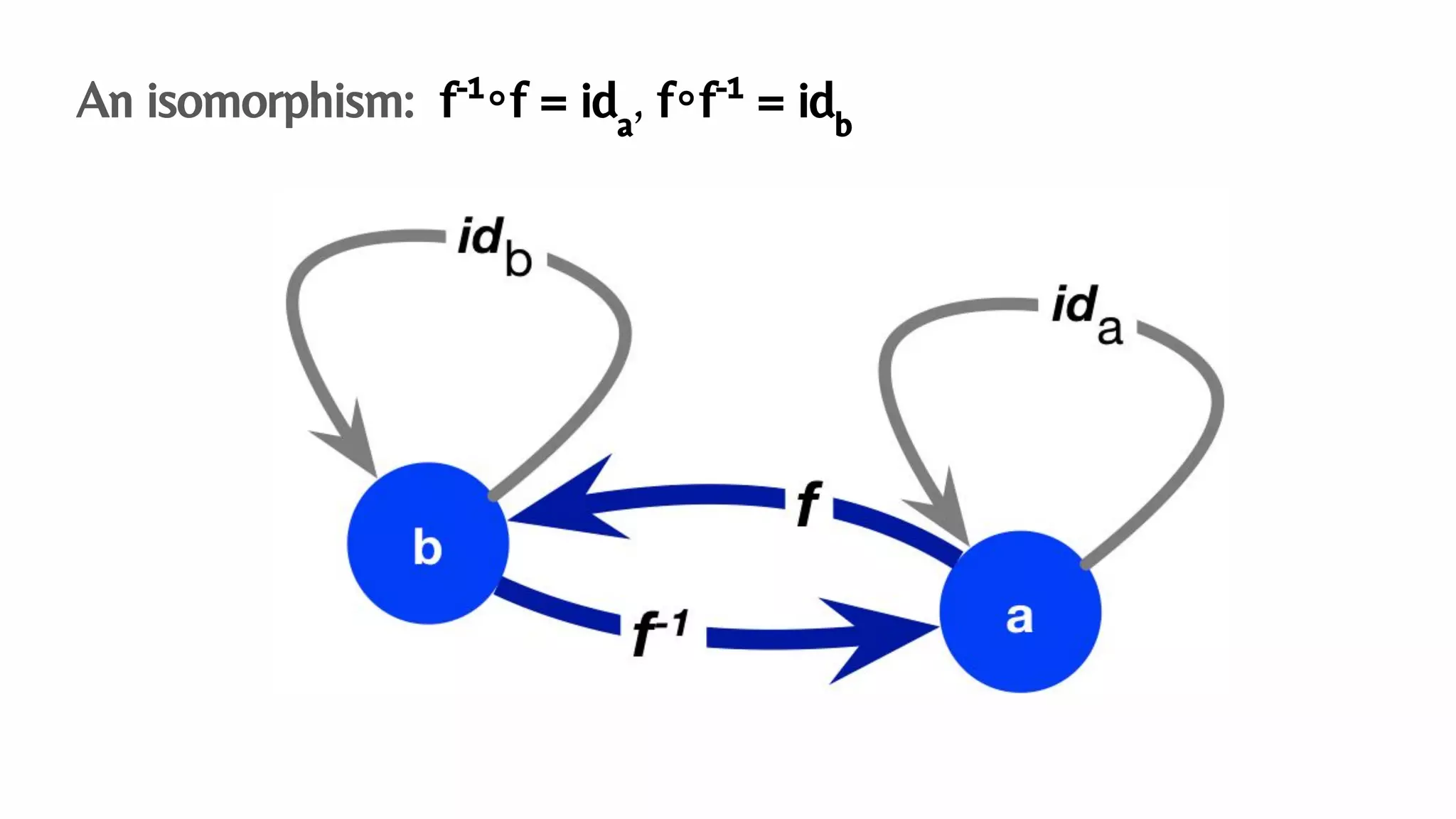
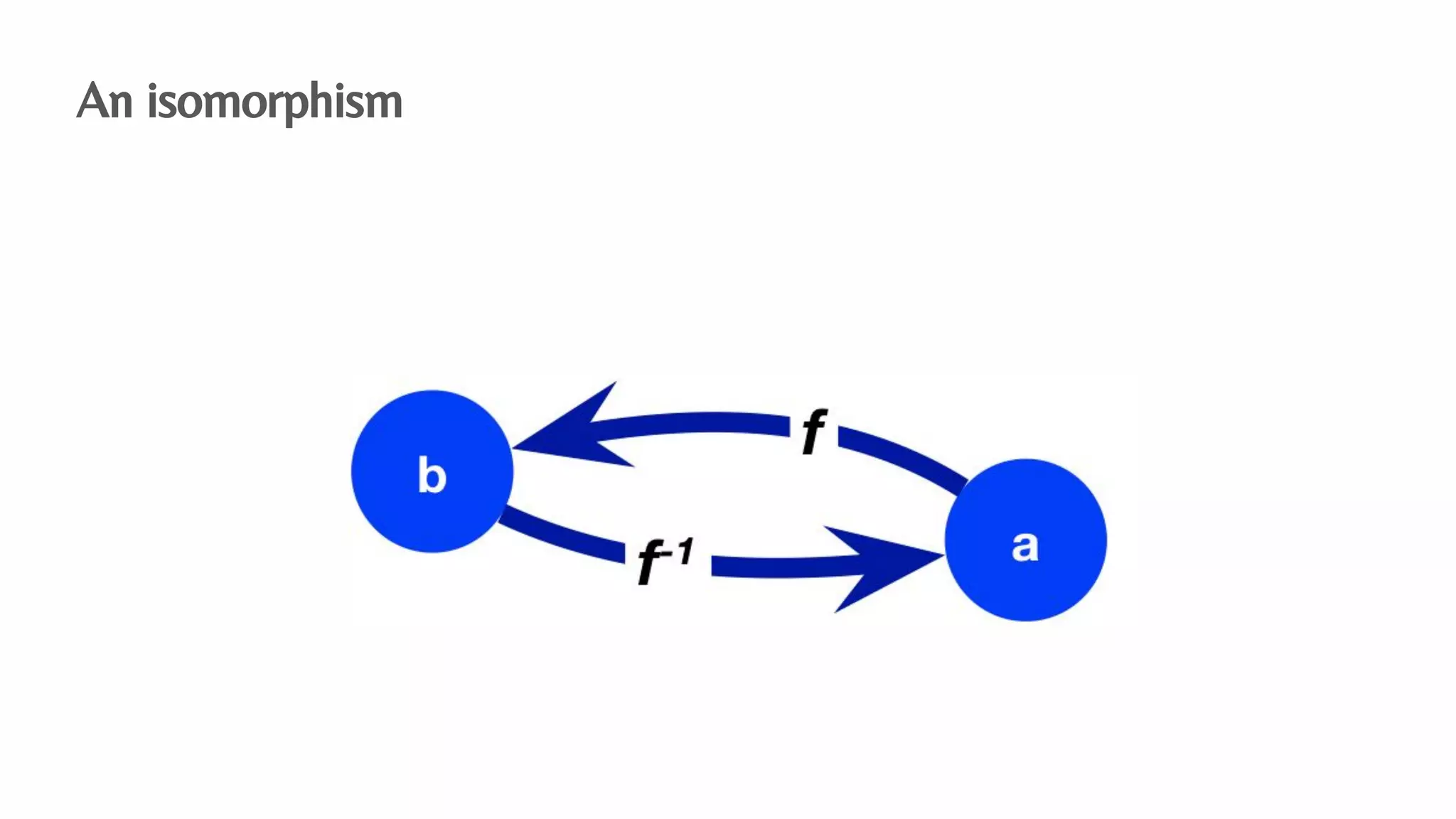
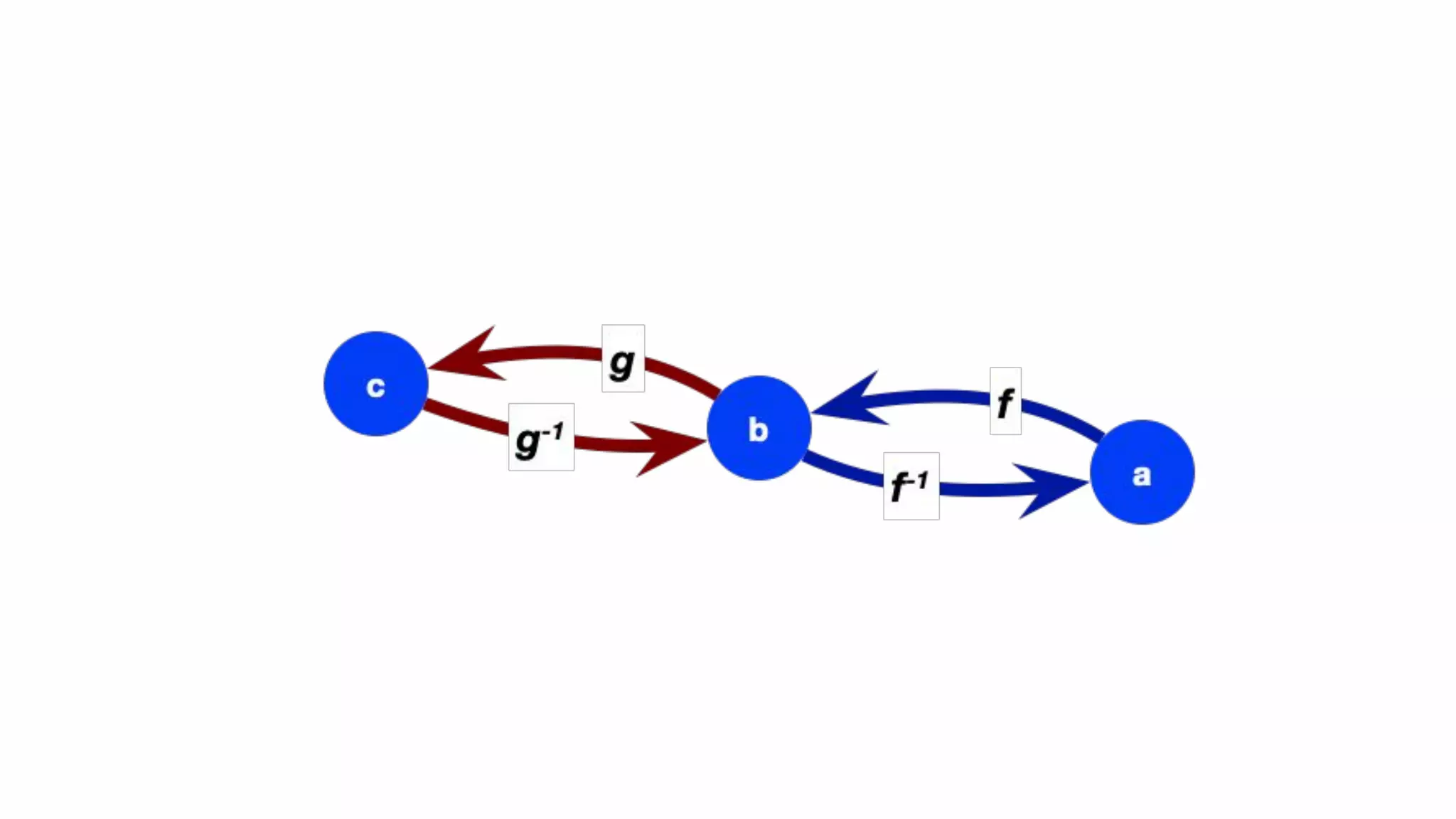
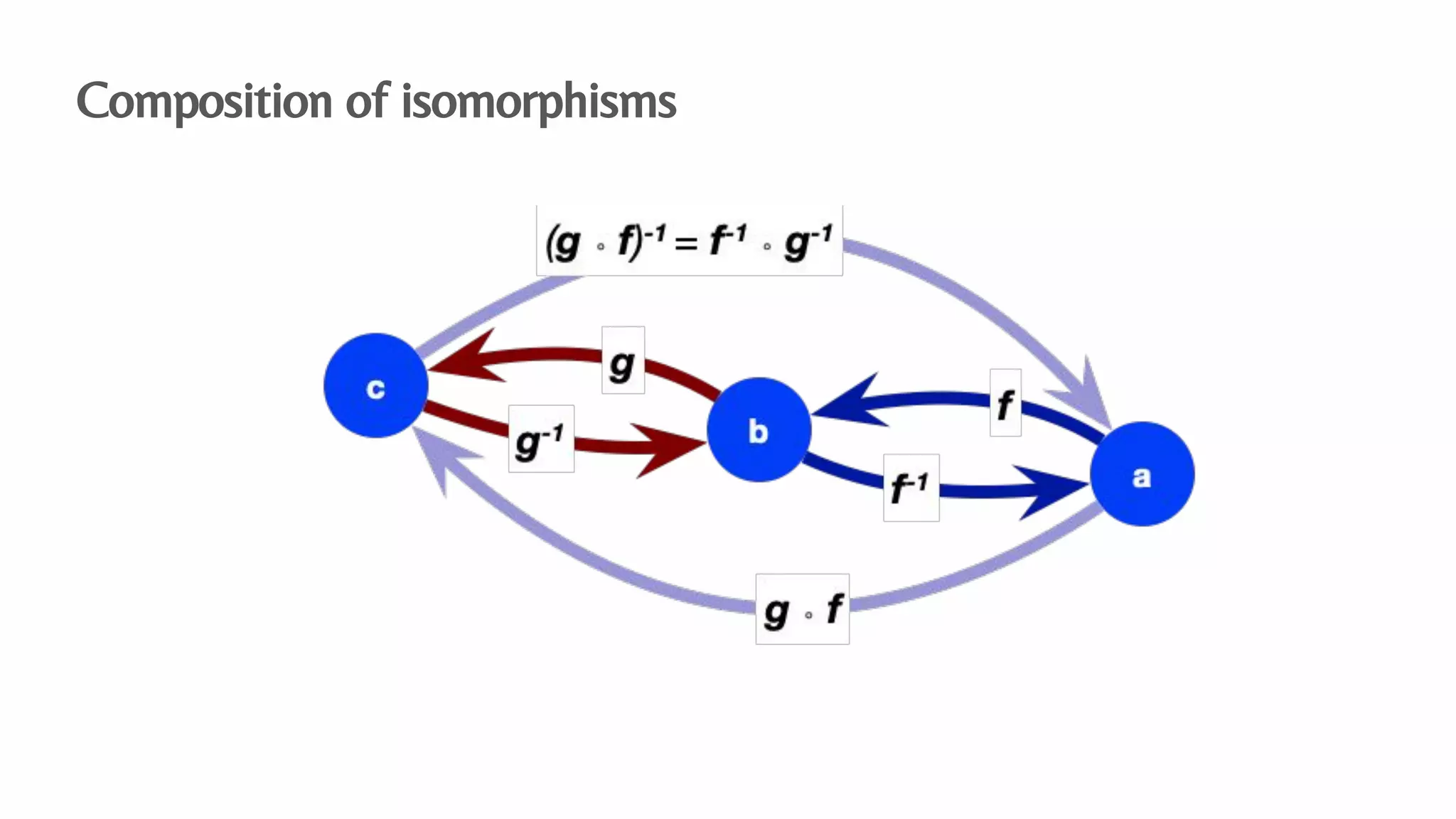
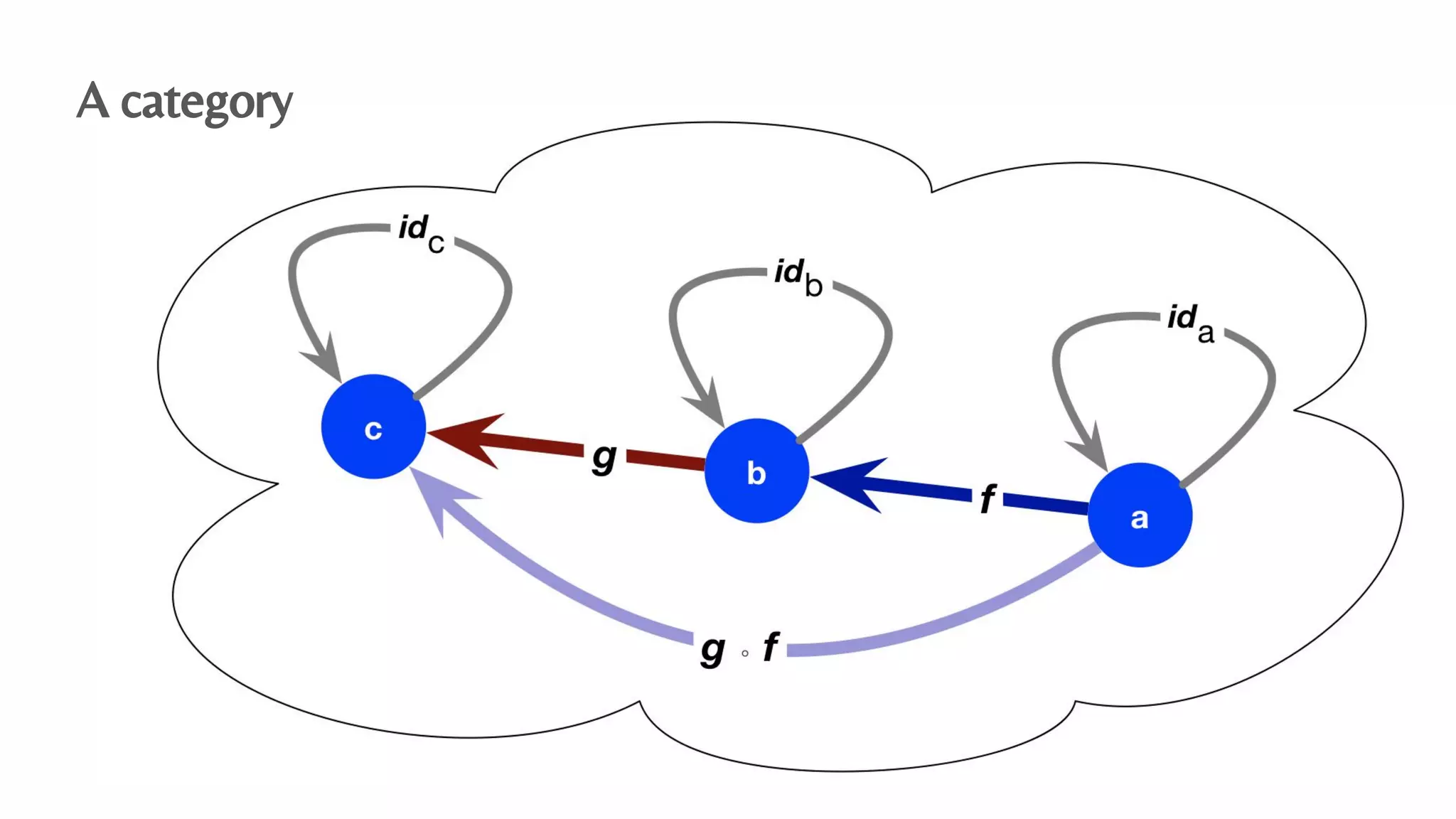
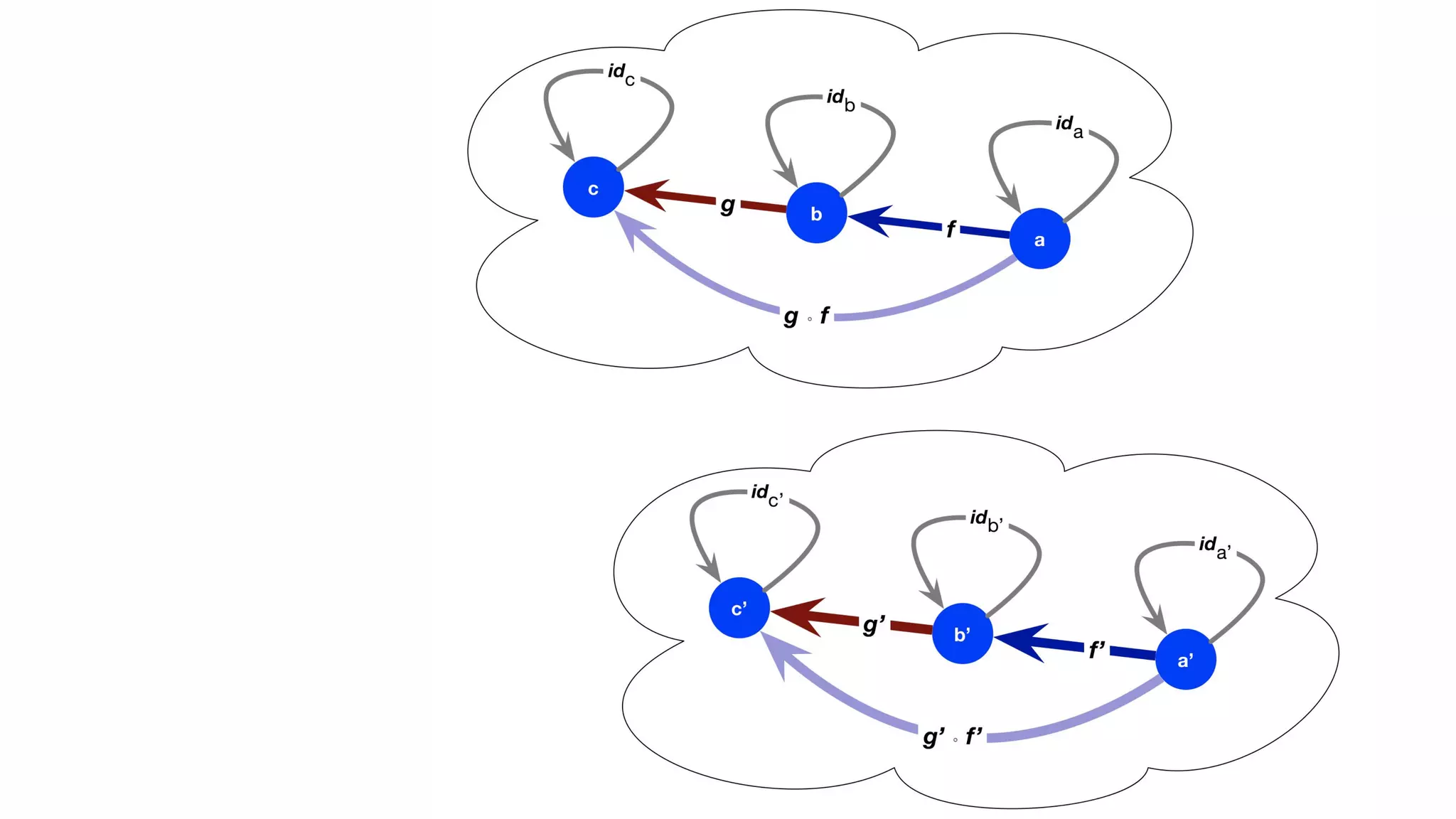
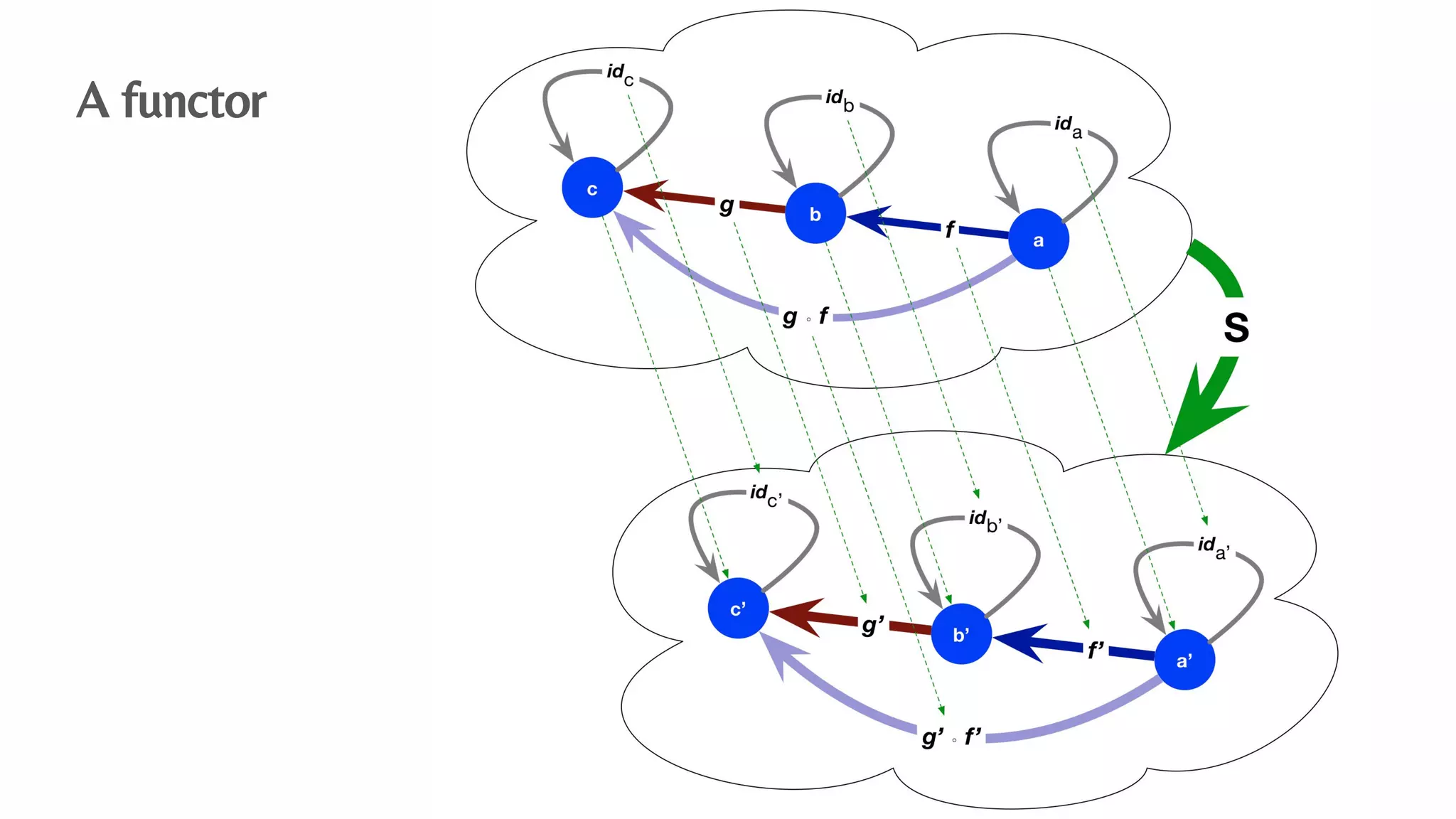
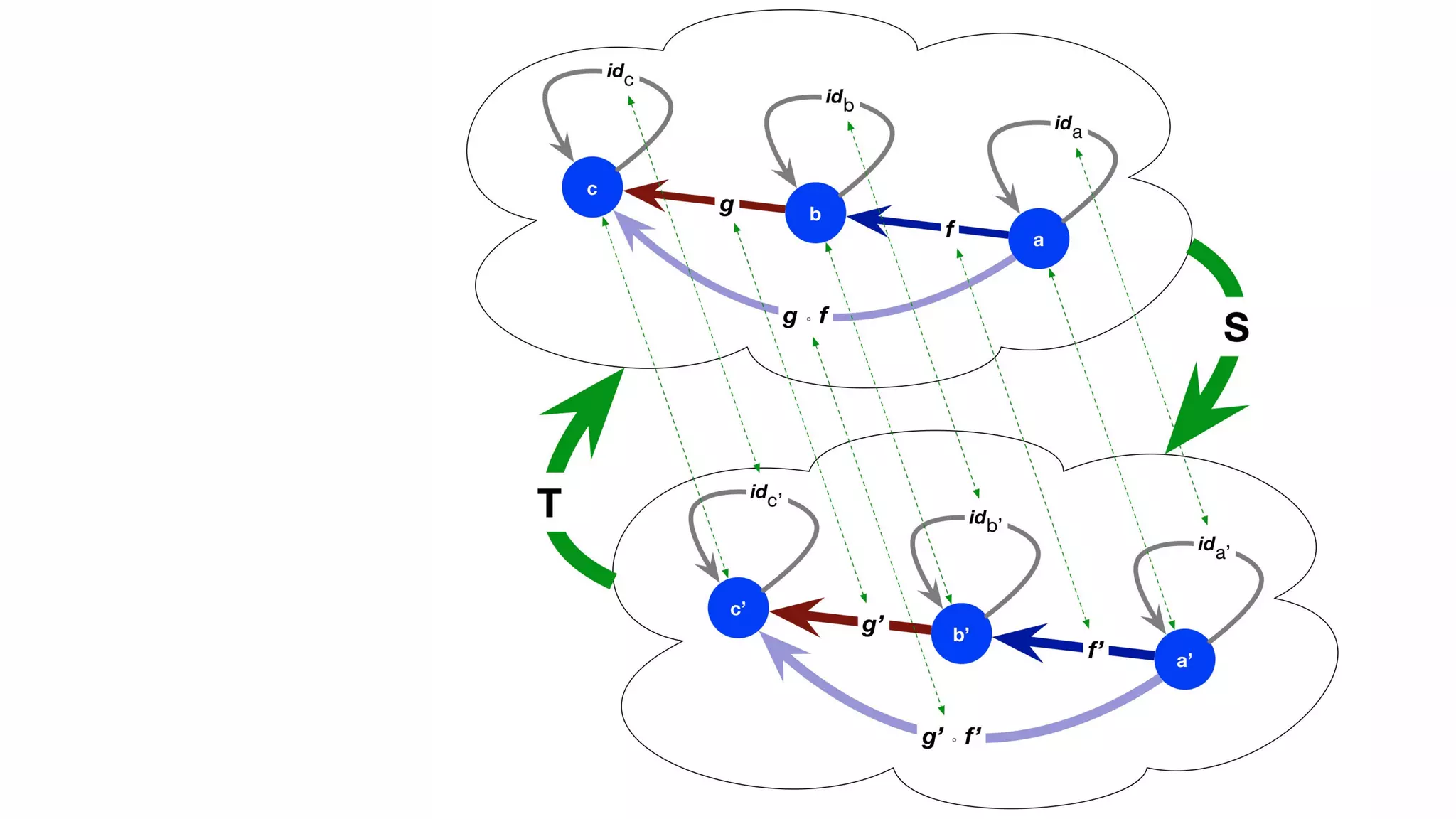
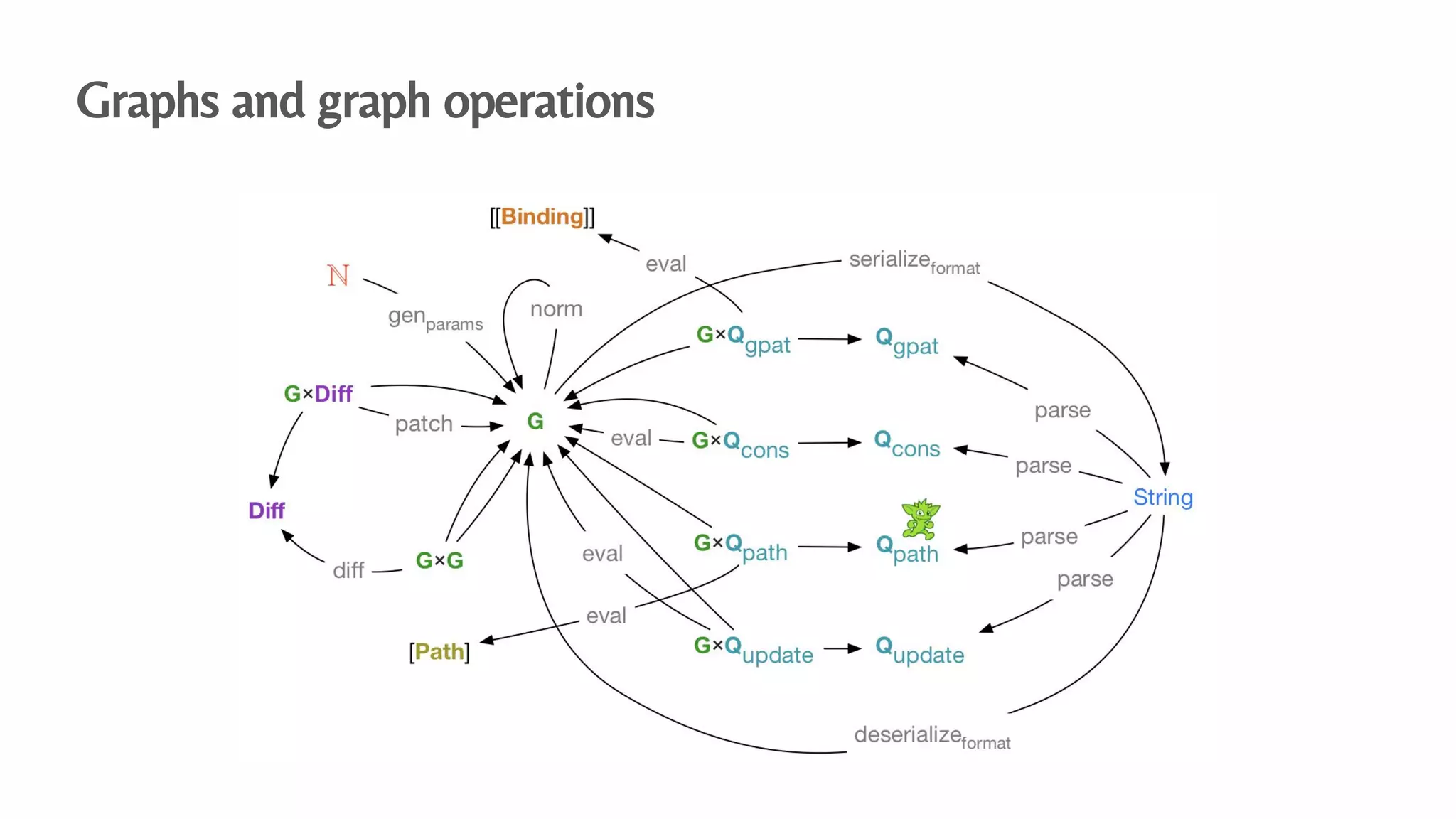
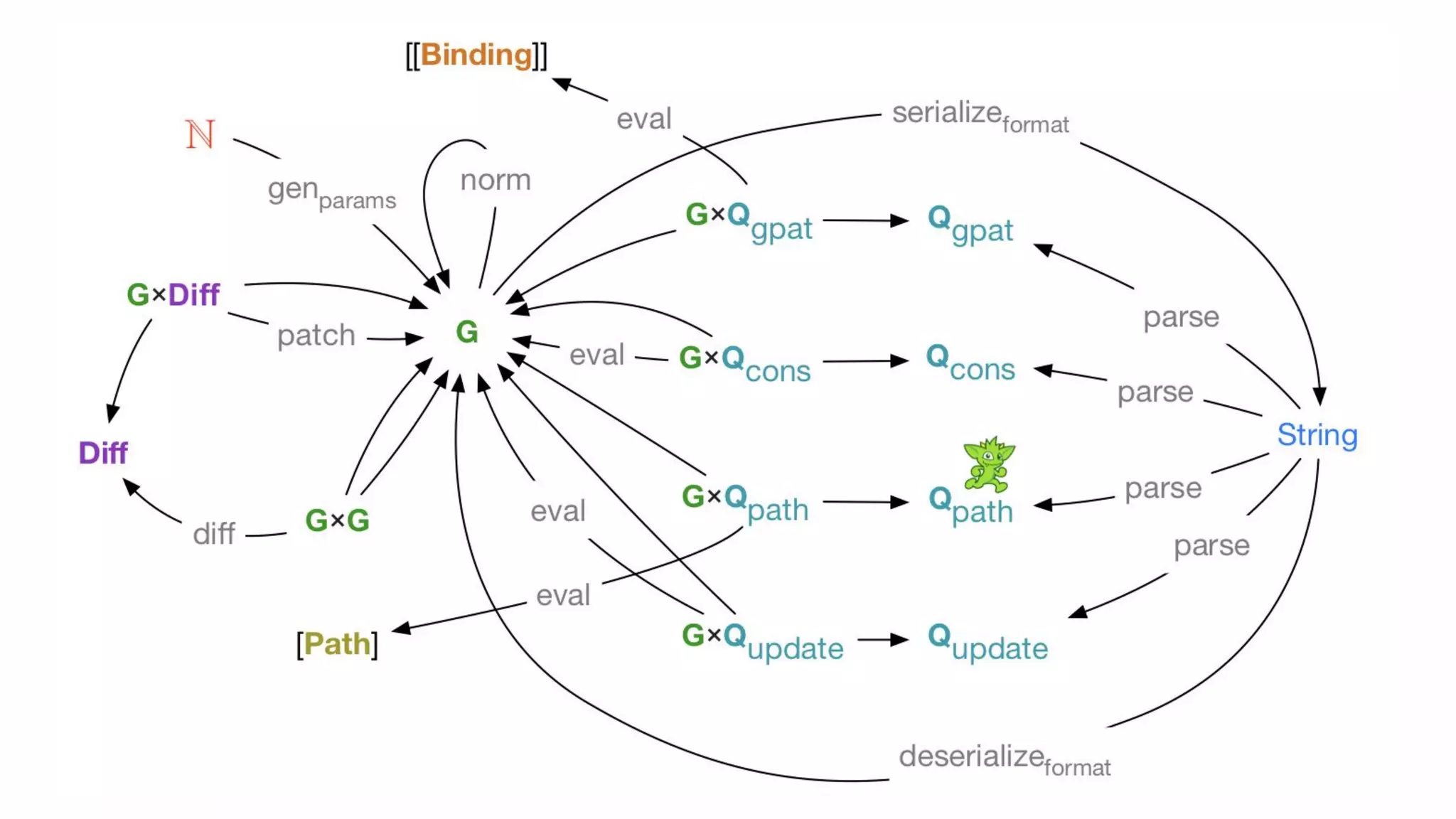
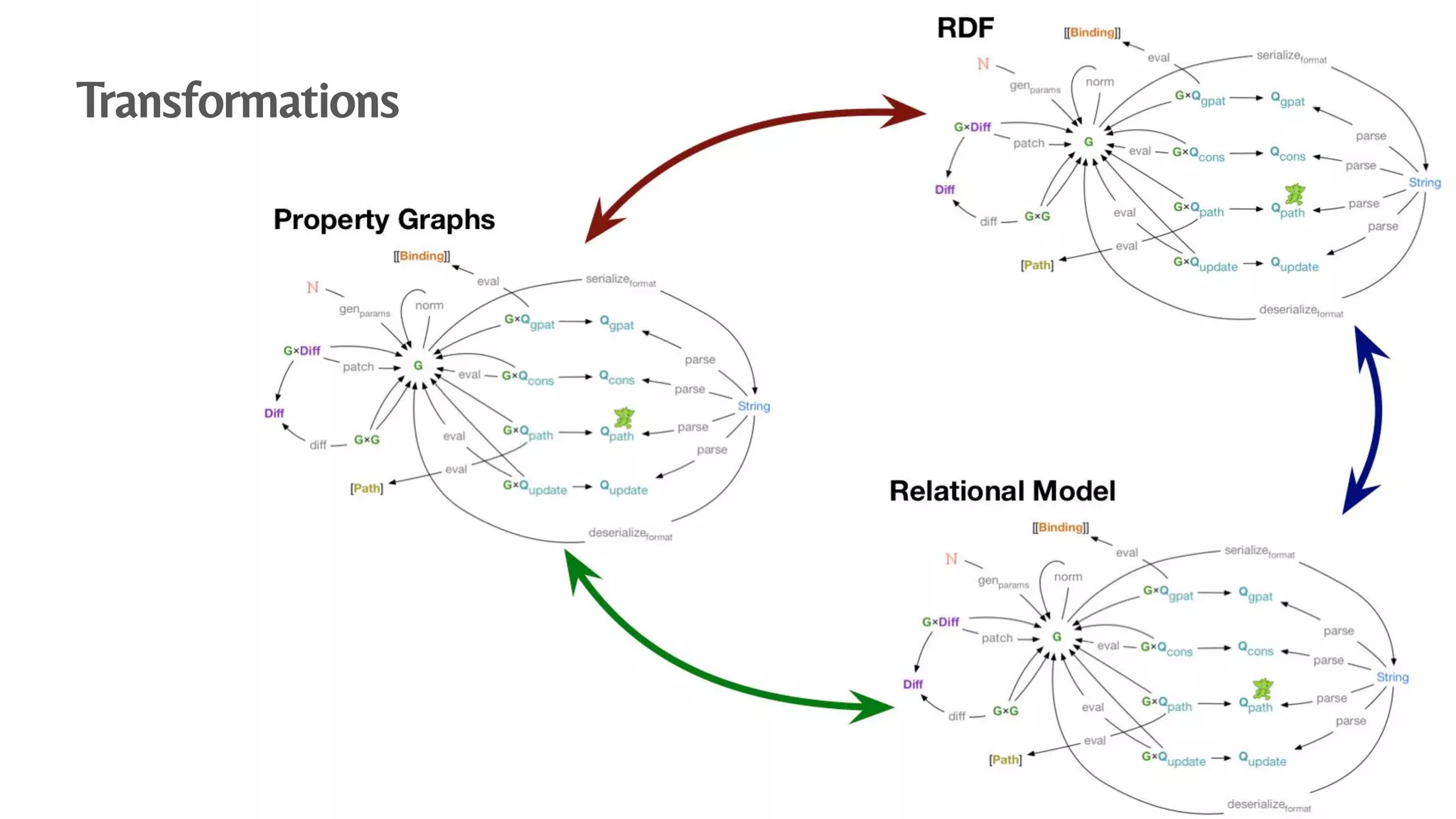
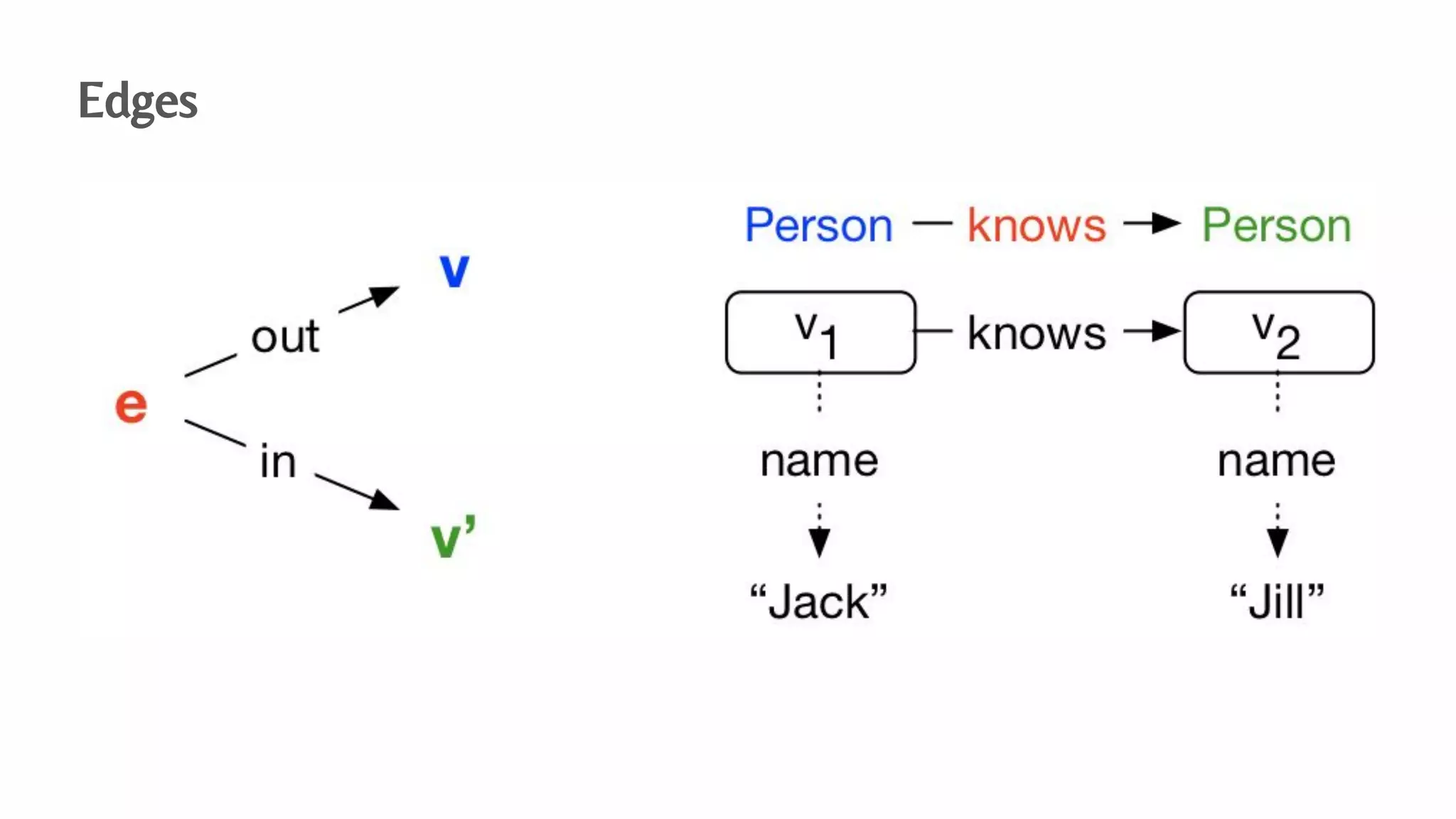
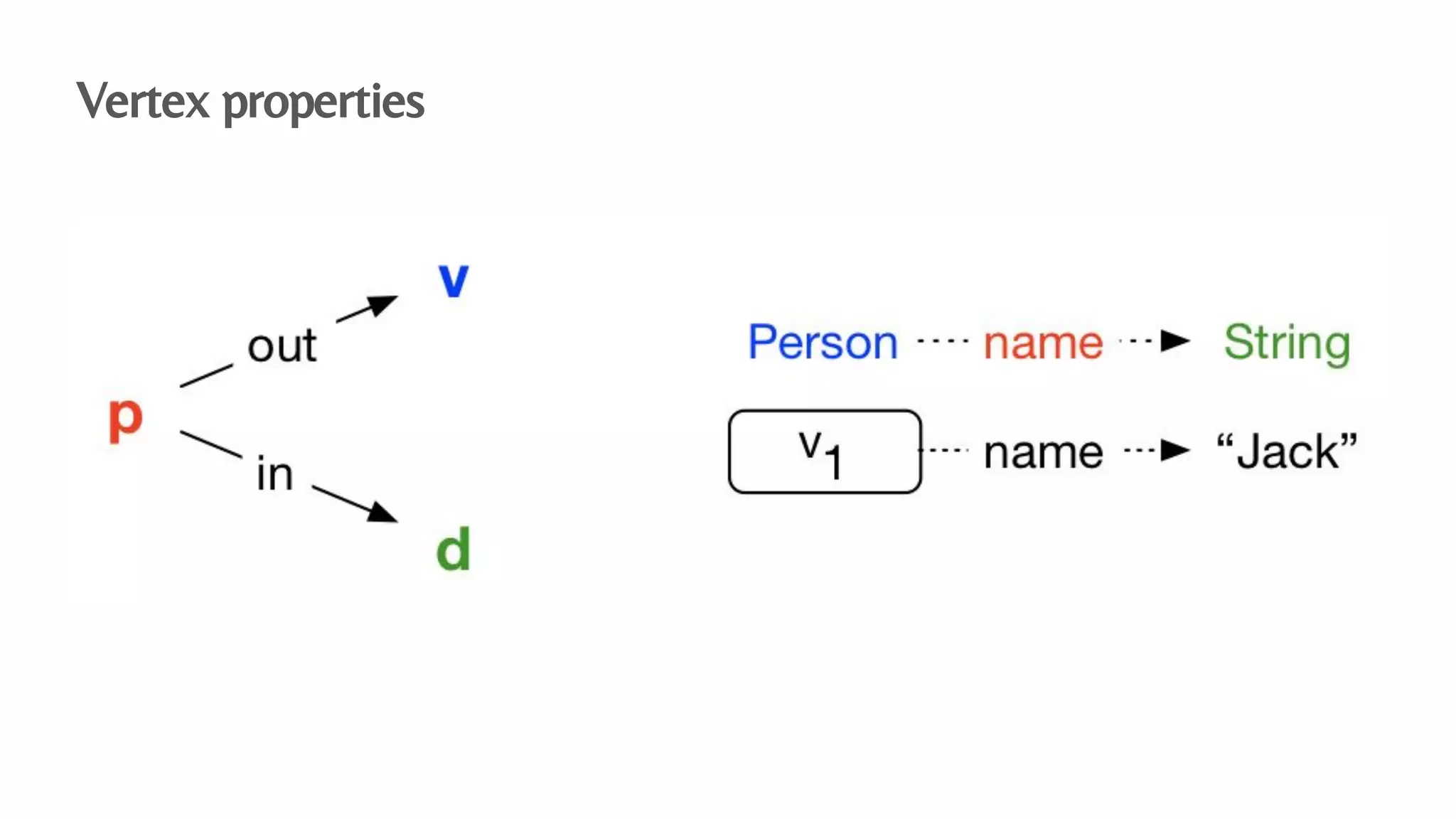
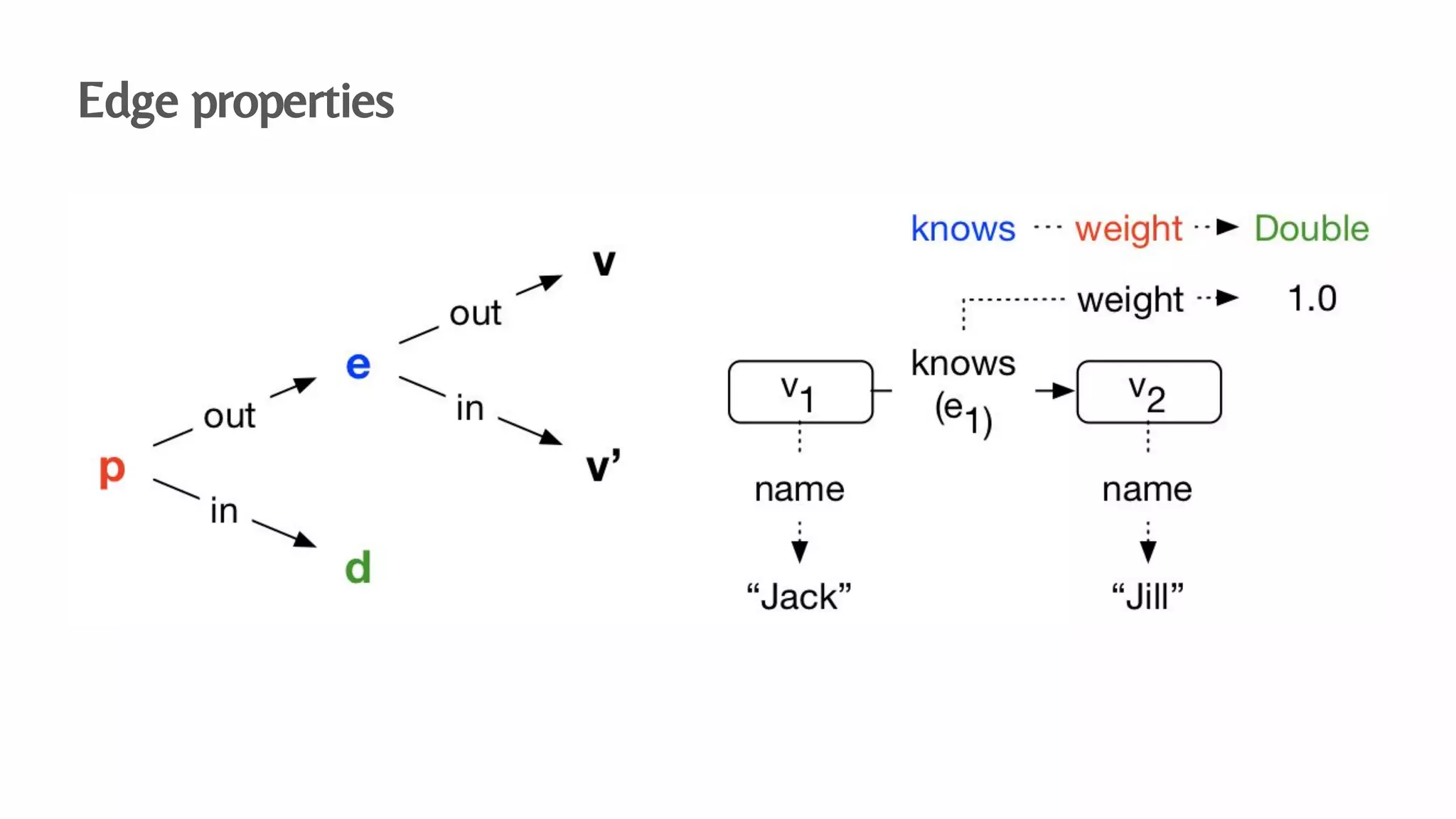
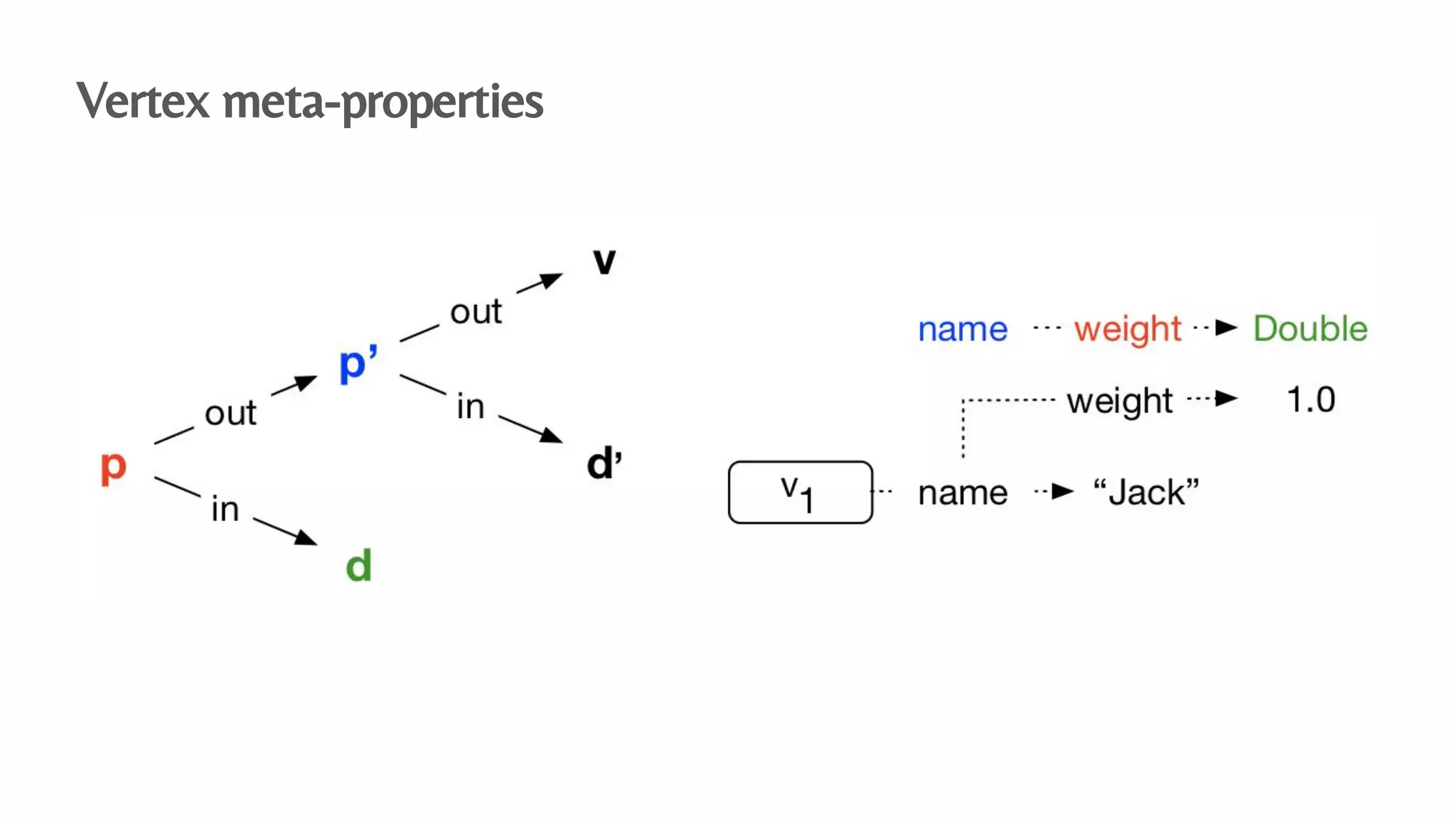
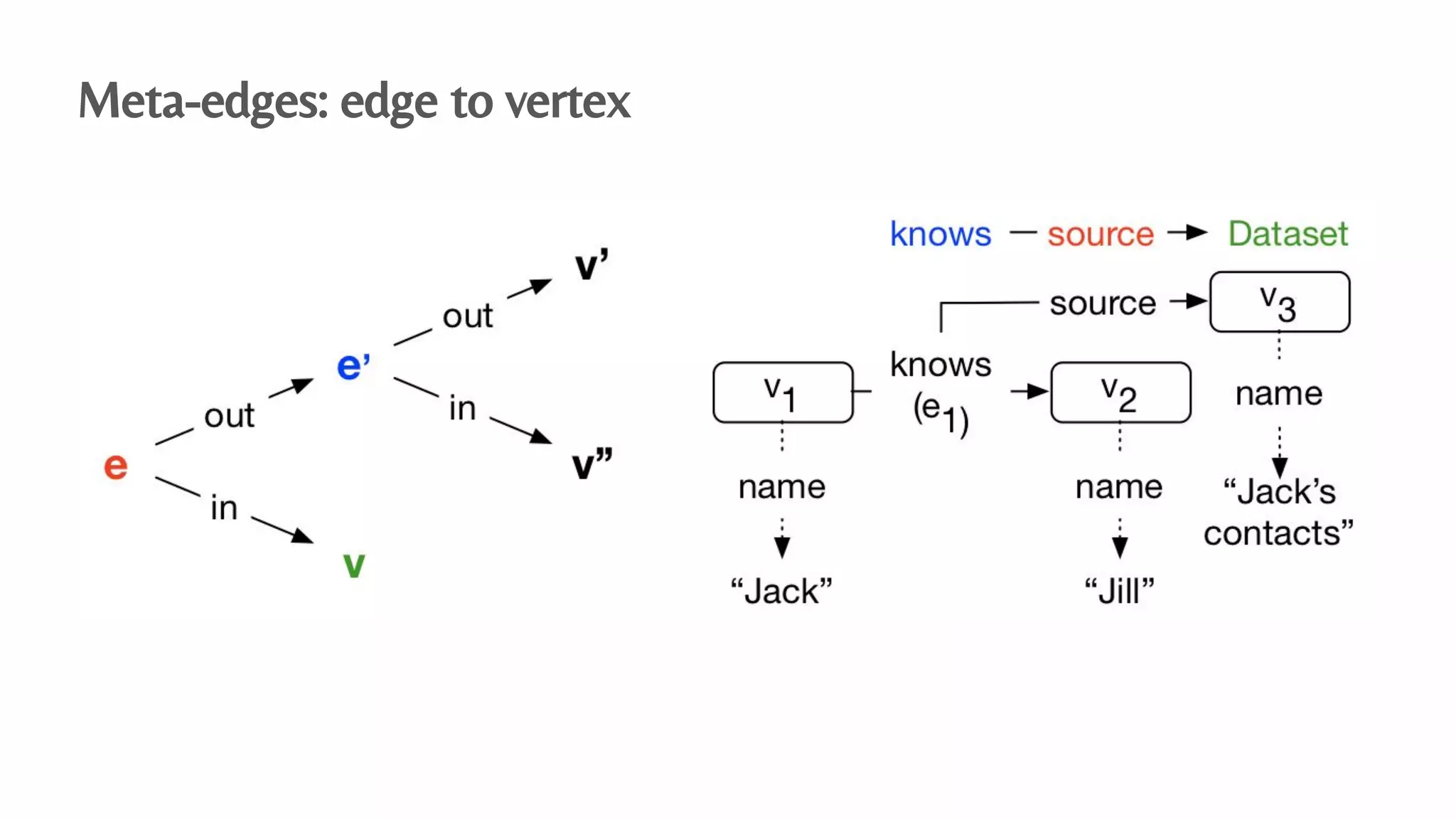
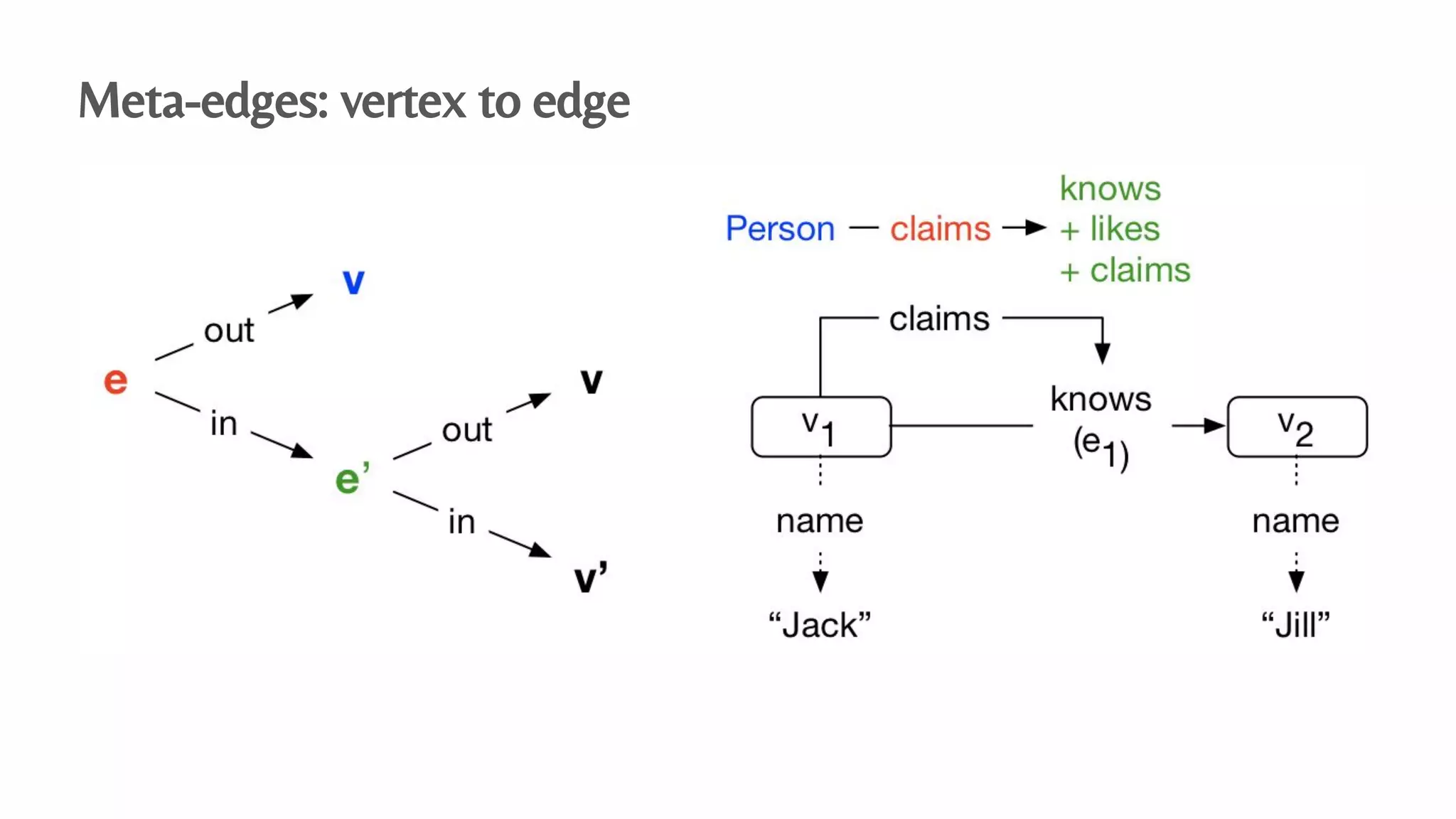
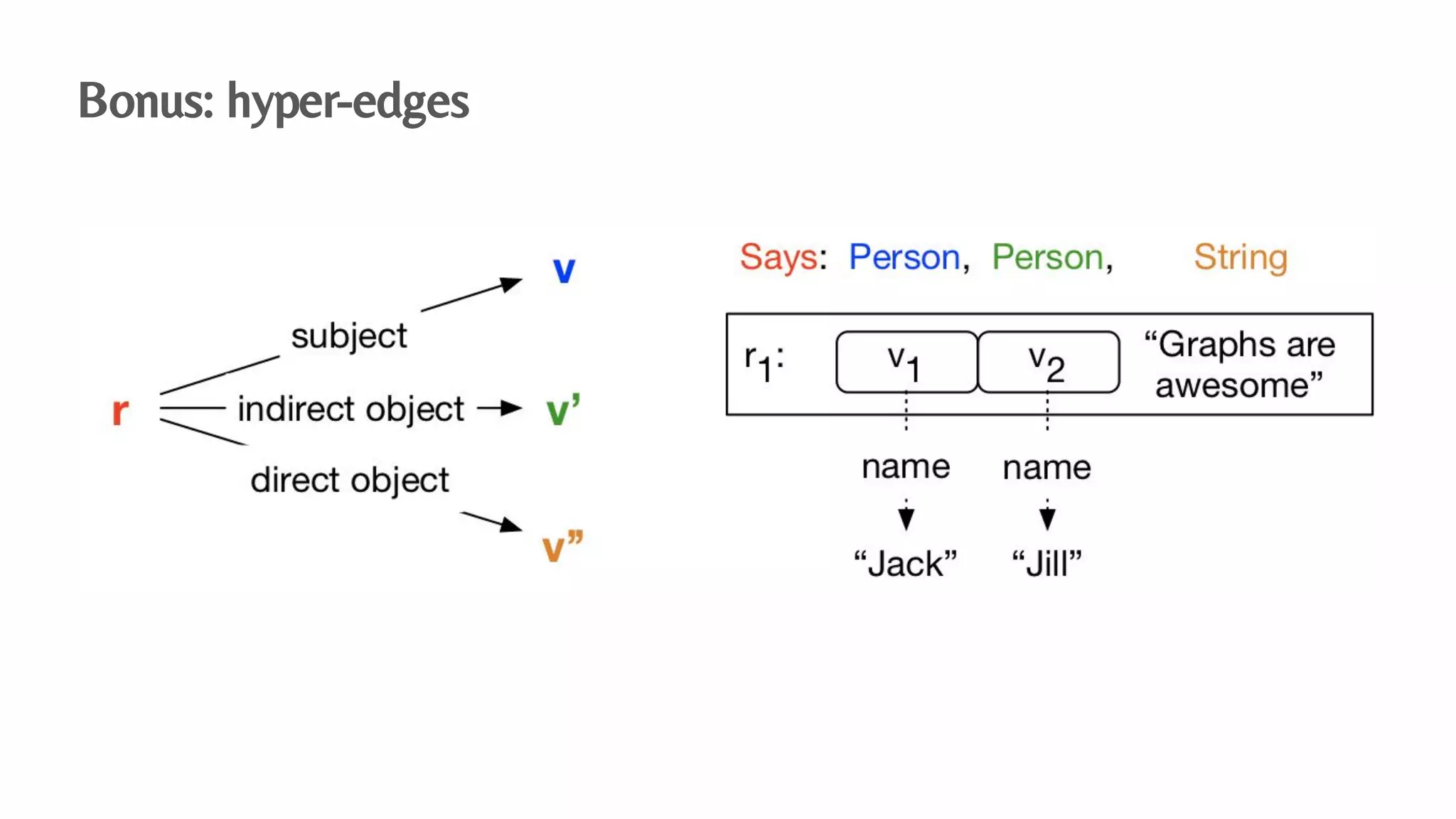
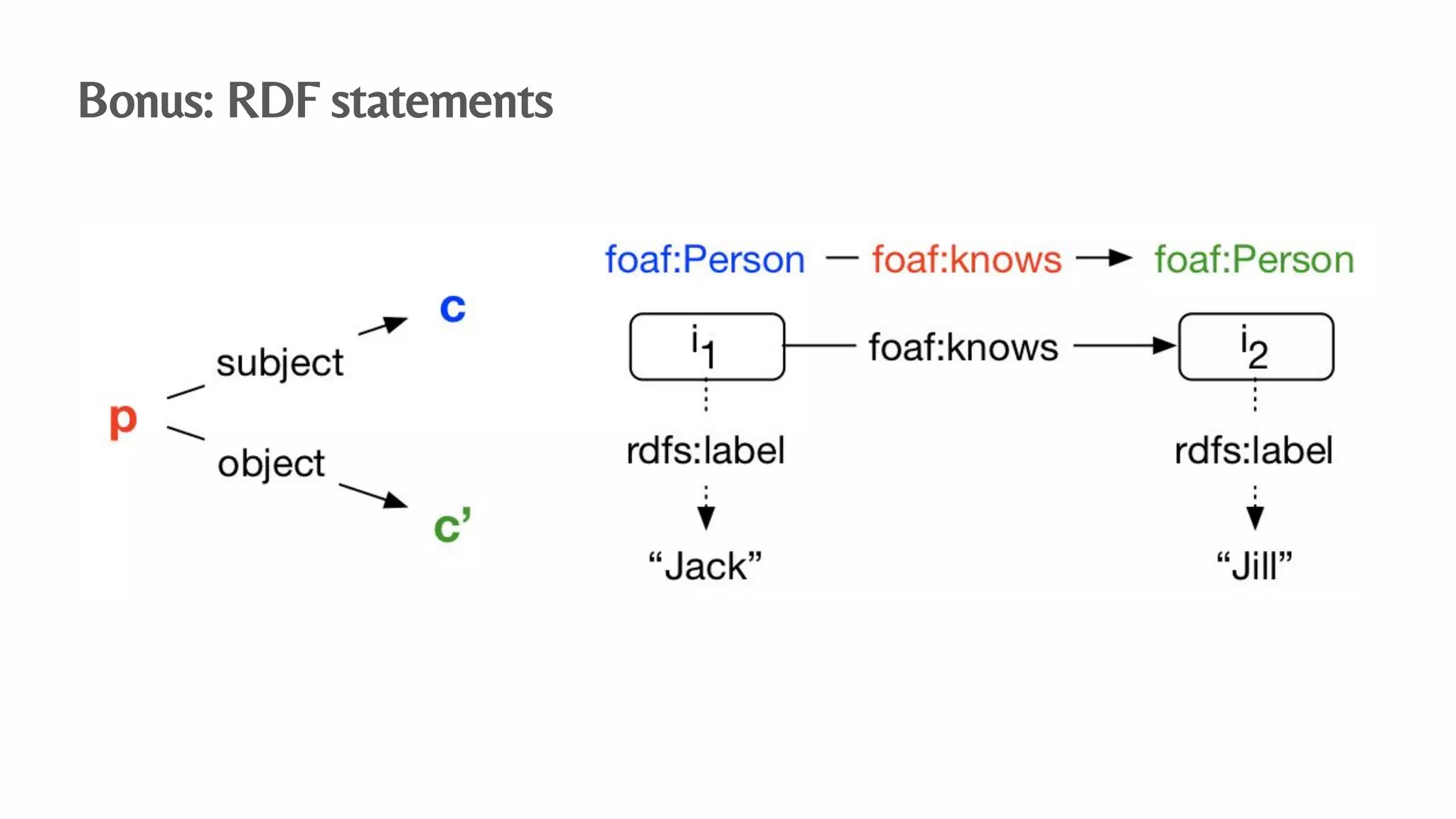
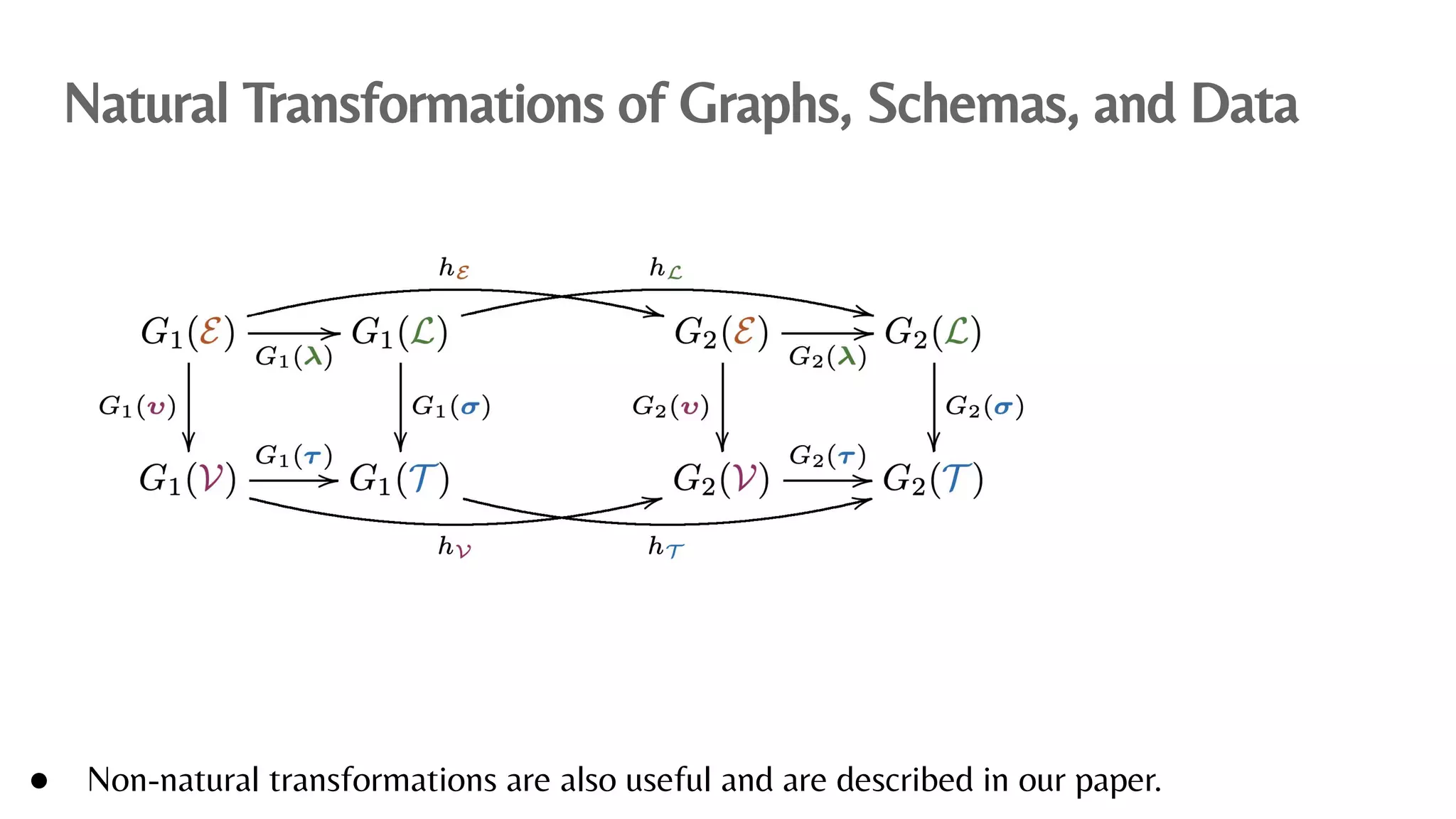
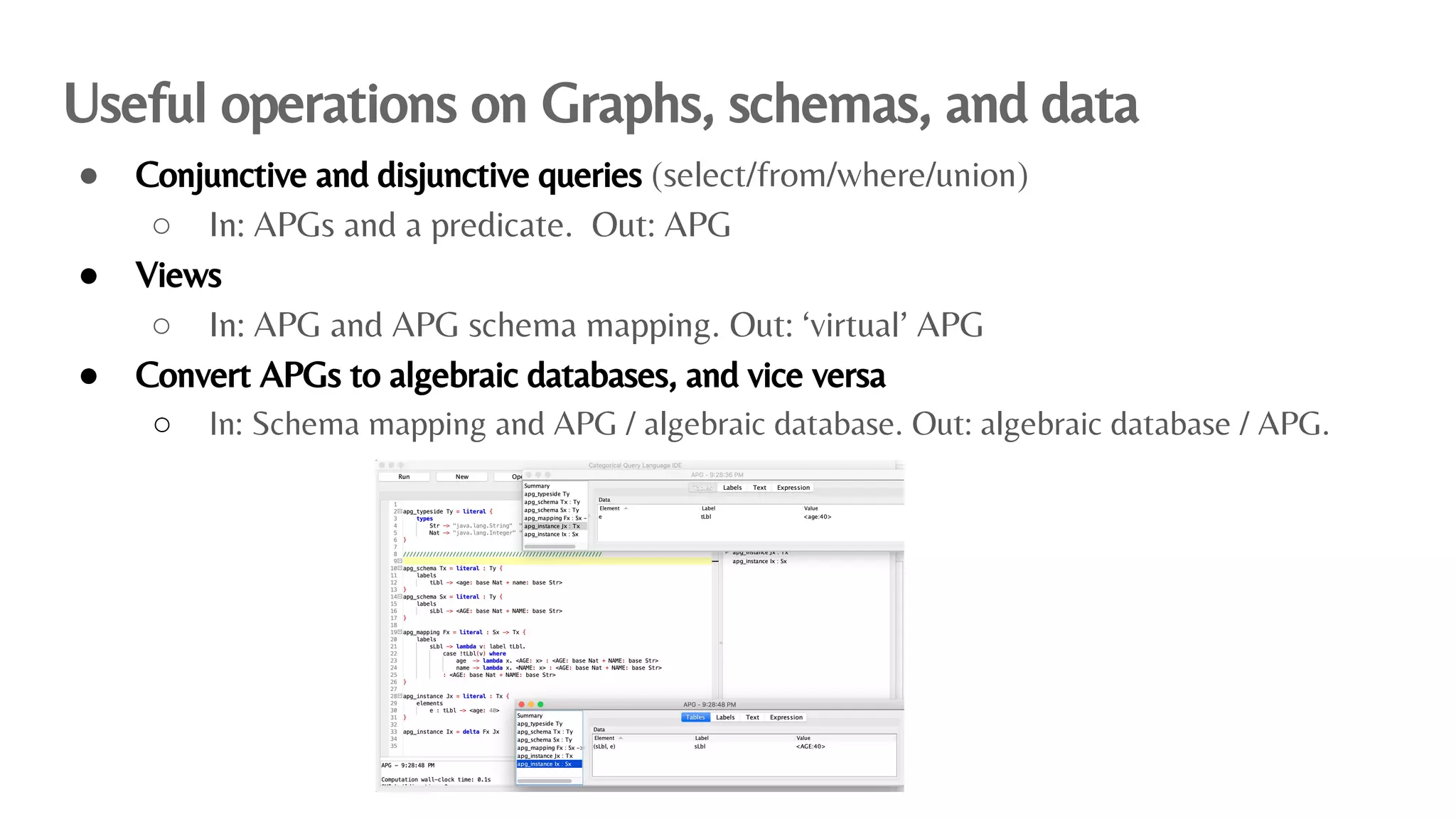
The document presents an algebraic data model for graphs and hypergraphs, focusing on key concepts from category theory and their application in data modeling. It discusses various data models, including property graphs, and introduces algebraic property graphs that emphasize formal schemas and mapping languages, as well as integration frameworks. Additionally, the document outlines operations on graphs and provides insights into transformations and properties relevant for enterprise data management.

1. An Algebraic Data Model for Graphs and Hypergraphs
Bonus Intro to Category Theory
November 21, 2019
Joshua Shinavier, PhD (Uber)

2. • Graphs
• Categories
• Data Models
• Algebraic Property Graphs
Outline

3. Graphs

15. TinkerFactory.createClassic() + vertex labels

16. Graph structure

17. Categories

19. An object

20. An arrow (morphism)

22. Composition

23. Associativity

25. Identity

27. An isomorphism

28. An isomorphism: f-1
∘f = ida
, f∘f-1
= idb

29. An isomorphism

31. Composition of isomorphisms

32. A category

34. A functor

36. Graphs and graph operations

38. Transformations

39. Data models

40. • Property Graphs
• Resource Description Framework (RDF)
• Relational Model
• SQL, CQL, HQL, DQL, ...
• Data interchange formats
• Protocol Buffers, Apache Thrift, Apache Avro
• Mostly based on algebraic data types (ADTs)
Some data models of interest (@ Uber)

41. • A simple interpretation1
I of an RDF graph is:
• A non-empty set IR of resources, called the domain or universe of I
• A set IP, called the set of properties of I
• A mapping IEXT from IP into 𝒫(IR x IR), i.e. the set of sets of pairs <x, y> with
x and y in IR
• Assuming:
• Ground RDF graphs only (⇒ no blank nodes)
Resource Description Framework (RDF)
1) World Wide Web Consortium. (2014). RDF 1.1 concepts and abstract syntax.

42. • Simple.
• Vertices, edges, properties
• No standard
• W3C Property Graphs working group (2013)
• W3C Graph Data Workshop (March 2019)
• Next best thing?
• TinkerPop’s Graph.Features
Property Graph data model

43. • Many are concerned with the data model
• Vertex/edge id data types
• Numeric, string, UUID, “any”
• Property support
• Supports vertex properties? edge properties? vertex metaproperties?
• Multi-properties?
• Property data types
• Primitive: boolean, byte, double, float, integer, long, string
• Complex: array, map, list (uniform/mixed), serializable
TinkerPop’s Graph.Features

44. Property graph objects
v = a vertex label (e.g. Person, Place, Dataset)
e = an edge label (e.g. knows, likes, claims)
p = a property key (e.g. name, weight)
d = a data type (e.g. String, Integer, List<String>)

45. Edges

46. Vertex properties

47. Edge properties

48. Vertex meta-properties

49. Meta-edges: edge to vertex

50. Meta-edges: vertex to edge

51. Bonus: hyper-edges

52. Bonus: RDF statements

53. Algebraic Property Graphs

54. A formal data model for enterprise Property Graphs
● Things we need
○ Formal schema & mapping language for property graphs
○ Framework for graph transformation and integration
○ Means to build virtual graphs out of non-graph datasets (and vice versa)
● Algebraic Property Graphs
○ Based on algebraic data types
○ Strong connections to type theory, database theory, and category theory:
■ A familiar approach to type inference
■ Easy to reason about: all operations and proofs mechanically verified in Coq
■ Generalizes to algebraic databases

55. Product and sum types, identifiers, and values
● APG:
● Thrift example:

56. Algebraic types in common data interchange languages

57. Graph, schema, and data

58. Natural Transformations of Graphs, Schemas, and Data
● Non-natural transformations are also useful and are described in our paper.

59. Taxonomy of graph elements
● Vertex: “no data”.
● Edge: ordered pair of elements.
● Property: ordered pair (element, value).
○ Vertex property: element is a vertex.
○ Edge property: element is an edge
○ Meta-property: element is another property
■ Vertex / edge metaproperty, etc.
● Alias: contains another element
○ Vertex or edge “tags”
○ Aliases for primitive data types
● Hyperelement: everything else

60. Useful operations on Graphs, schemas, and data
● Conjunctive and disjunctive queries (select/from/where/union)
○ In: APGs and a predicate. Out: APG
● Views
○ In: APG and APG schema mapping. Out: ‘virtual’ APG
● Convert APGs to algebraic databases, and vice versa
○ In: Schema mapping and APG / algebraic database. Out: algebraic database / APG.

61. Thanks
● joshsh@uber.com
● ryan@conexus.ai
https://arxiv.org/abs/1909.04881
(submitted to ICDT)