Dokumen ini membahas berbagai algoritma pengurutan, termasuk selection sort, insertion sort, merge sort, dan quicksort, serta prinsip dasar di balik pemrograman dan penerapan algoritma pengurutan. Metode sorting ini digunakan untuk menyusun data secara efisien dan memudahkan pencarian. Selain menjelaskan proses yang mendasari setiap algoritma, dokumen juga memberikan contoh implementasi dalam kode.

2. Topik
 Sorting
 Selection Sort
 Straight insertion Sort
 Merge Sort
 Paradigma Divide-and-Conquer
 Quicksort
 Paradigma Divide-and-Conquer

3.  Algoritma pengurutan adalah algoritma untuk
meletakkan kumpulan elemen data ke dlm urutan
tertentu, berdasarkan satu atau beberapa kunci ke dalam
tiap-tiap elemen

4. • Mengatur elemen berdasar urutan tertentu
• Digunakan secara luas dalam aplikasi
• Beberapa algoritma sorting telah dibuat karena
proses tersebut sangat mendasar dan
sering digunakan

5. Memudahkan dalam pencarian & memudahkan
dalam melihat data
Contoh : Kamus, buku telepon, kartu berobat, kartu
perpustakaan, dst

6.  Algoritma sorting yang lainnya
 Intuitif dan mudah diimplementasikan
 Juga mirip dengan cara lain dalam pengurutan kartu
 Tujuan: mengurutkan kartu secara ascending
 Diberikan: kartu, meja
 Awal: Kartu disebar secara acak pada tabel
 Periksa nilai, kemudian pilih kartu dengan nilai terendah
 Tukarkan posisi kartu ini dengan kartu pertama pada meja
 Cari kartu dengan nilai terendah dari sisa kartu yang ada
 Tukarkan kartu terpilih dengan kartu pada posisi kedua
 Ulangi proses hingga kartu kedua sebelum terakhir pada meja
dibandingkan dan ditukar dengan kartu terakhir

7.  Pilih elemen dengan nilai terendah
 Tukarkan elemen terpilih dengan elemen pada posisi ke - i
 i dimulai dari 1 hingga n
 Dimana n adalah total elemen yang ada dikurangi 1

8. 1 void selectionSort(Object array[], int startIdx,
2 int endIdx) {
3 int min;
4 for (int i = startIdx; i < endIdx; i++) {
5 min = i;
6 for (int j = i + 1; j < endIdx; j++) {
7 if (((Comparable) array[min]).compareTo(
8 array[j])>0) {
9 min = j;
10 }
11 }
12 swap(array[min], array[i]);
13 }
14 }

10. Data di cek satu persatu mulai
dari yang kedua sampai dengan
yang terakhir, apabila ditemukan
data yang lebih kecil, daripada
data sebelumnya, maka data
tersebut disisipkan pada posisi
yang sesuai.

11. i=2,N
data[j+1]=x
x=data[i]
data[0]=x
j=i-1
t
x<data[j]
y
data[j+1]=data[j]
dec(j)

12. Merge Sort:
Paradigma Divide-and-Conquer
 Menggunakan rekursi dalam penyelesaiannya :
 Permasalahan awal dipilah menjadi sub-masalah
 Solusi atas sub-masalah menuntun menuju permasalahan utama
 3 Langkah:
 Divide
 Membagi permasalahan menjadi submasalah
 Conquer
 Menyelesaikan sub-masalah secara rekursif
 Jika sub-masalah cukup sederhana dan kecil, selesaikan secara
langsung
 Combine
 Kombinasikan solusi dari sub-masalah yang ada, hingga mencapai
permasalahan utama

13. Merge Sort: Algoritma
 Menggunakan pendekatan divide-and-conquer
 Divide
 Membagi elemen data menjadi dua bagian
 Conquer
 Selesaikan tiap bagian secara rekursif dengan memanggil
method mergeSort.
 Combine
 Kombinasikan dua bagian secara rekursif untuk
mendapatkan urutan yang diharapkan
 Rekursi selesai pada saat sisa dari sebagian elemen yang akan diurutkan
tepat tersisa satu
 Telah terurutkan

14. Merge Sort: Algoritma
1 void mergeSort(Object array[], int startIdx,
2 int endIdx) {
3 if (array.length != 1) {
4 Divide the array into two halves,
5 leftArr and rightArr
6 mergeSort(leftArr, startIdx, midIdx);
7 mergeSort(rightArr, midIdx+1, endIdx);
8 combine(leftArr, rightArr);
9 }
10 }

15. Merge Sort: Contoh

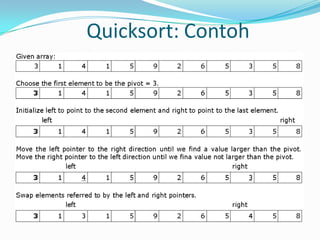
16. Quicksort: Algoritma
 Ditemukan oleh C.A.R. Hoare
 Berdasar pada paradigma divide-and-conquer
 Divide
 Bagi array menjadi dua subarray A[p...q-1] dan A[q+1...r] dimana
A[p...q-1] adalah kurang dari atau sama dengan A[q] dan elemen
pada A[q+1...r] adalah lebih dari atau sama dengan A[q]
 A[q] disebut sebagai pivot
 Perhitungan q adalah bagian dari prosedur pemisahan
 Conquer
 Urutkan subarray tersebut dengan memanggil method quickSort
secara rekursif
 Tak perlu melakukan proses “Combine”
 Subarrays telah terurutkan

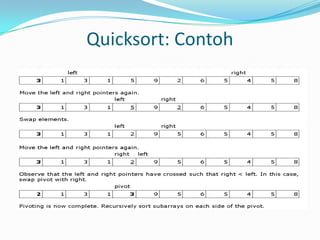
17. Quicksort: Algoritma
1 void quickSort(Object array[], int leftIdx,
2 int rightIdx) {
3 int pivotIdx;
4 /* Termination condition! */
5 if (rightIdx > leftIdx) {
6 pivotIdx = partition(array, leftIdx,
rightIdx);
7 quickSort(array, leftIdx, pivotIdx-1);
8 quickSort(array, pivotIdx+1, rightIdx);
9 }
10 }

18. Quicksort: Contoh

19. Quicksort: Contoh

20. Kesimpulan
 Teknik Sorting sederhana
 Insertion Sort
 Selection Sort
 Paradigma Divide-and-Conquer
 Merge Sort
 Quicksort