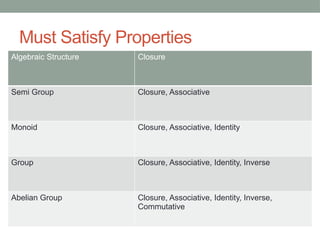
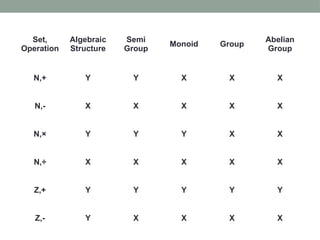
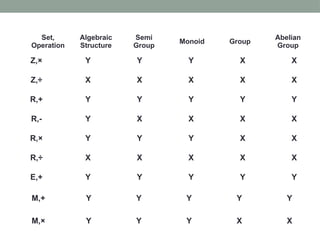
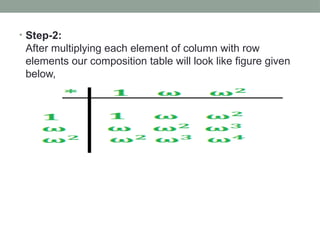
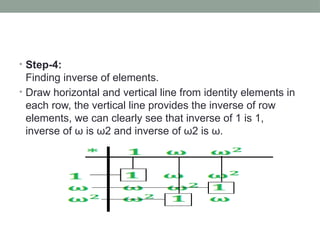
The document explains algebraic structures, focusing on sets with operations that satisfy specific algebraic laws, such as closure, associativity, identity, and inverses. It categorizes these structures into semigroups, monoids, groups, and abelian groups, providing definitions and examples for each. Additionally, it includes problems demonstrating how to validate these structures using properties and composition tables.

1. ALGEBRAIC
STRUCTURE
An algebraic structure is a set equipped with an operation
(or operations) that satisfy a standard set of algebraic
laws. For example, the set could be the set of all real
numbers and the operations could be addition and
multiplication (and their inverses, subtraction and division)

2. Applications of Group Theory
• In Physics, it plays an indispensable role in the determination of the selection
rules for spectroscopic transitions in Atomic and Molecular Spectroscopy.
• In Chemistry, it is implemented to study and analyze the symmetries and the
crystal structures of molecules, including many physical and chemical
properties, and spectroscopic properties of the molecule. The group theory
has turned out to be a standard and a powerful tool for studying molecular
properties in the terms of molecular orbital theory.
• Group theory, being an eventual and powerful tool for symmetry, has an
ultimate impact on research in robotics, computer vision, computer graphics
and medical image analysis.
• In Mathematics, it can be used for classification of identical mathematical
objects that possess symmetry, for example in geometric figures ( a circle is
highly symmetric and invariant under any rotation) and in mathematical
functions and operations.
• For the smooth data transmission, the concept of group, subgroups and
cosets are used in Cryptography and Public Key algorithms.

3. BINARY OPERATIONS
• Binary operations on a set are calculations that combine
two elements of the set (called operands) to produce
another element of the same set.
• The binary operations * on a non-empty set A
are functions from A × A to A. The binary operation, *: A ×
A → A. It is an operation of two elements of the set
whose domains and co-domain are in the same set.

4. Algebraic Structure
• A non empty set S is called an algebraic structure w.r.t
binary operation (*) if it follows following axioms:
• Closure:(a*b) belongs to S for all a ,b S.
∈
• Ex : S = {1,-1} is algebraic structure under *
• As 1*1 = 1, 1*-1 = -1, -1*-1 = 1 all results belongs to S.
•
• But above is not algebraic structure under + as 1+(-1) = 0
not belongs to S.

5. Semi Group
• A non-empty set S, (S,*) is called a semigroup if it follows
the following axiom:
• Closure:(a*b) belongs to S for all a, b S.
∈
• Associativity: a*(b*c) = (a*b)*c a, b ,c belongs to S.
∀
• Note: A semi group is always an algebraic structure.
• Ex : (Set of integers, +), and (Matrix ,*) are examples of
semigroup.

6. Monoid
• A non-empty set S, (S,*) is called a monoid if it follows the following
axiom:
• Closure:(a*b) belongs to S for all a, b S.
∈
• Associativity: a*(b*c) = (a*b)*c a, b, c belongs to S.
∀
• Identity Element: There exists e S such that a*e = e*a = a a S
∈ ∀ ∈
• Note: A monoid is always a semi-group and algebraic structure.
• Ex : (Set of integers,*) is Monoid as 1 is an integer which is also identity
element .
• (Set of natural numbers, +) is not Monoid as there doesn’t exist any
identity element. But this is Semigroup.
But (Set of whole numbers, +) is Monoid with 0 as identity element

7. Group
• A non-empty set G, (G,*) is called a group if it follows the
following axiom:
• Closure:(a*b) belongs to G for all a, b G.
∈
• Associativity: a*(b*c) = (a*b)*c a, b, c belongs to G.
∀
• Identity Element: There exists e G such that a*e = e*a = a
∈
a G
∀ ∈
• Inverses: a G there exists a
∀ ∈ -1
G such that a*a
∈ -1
= a-1
*a =
e
• Note:
• A group is always a monoid, semigroup, and algebraic
structure.
• (Z,+) and Matrix multiplication is example of group.

8. Abelian Group or Commutative group
• A non-empty set S, (S,*) is called a Abelian group if it
follows the following axiom:
• Closure:(a*b) belongs to S for all a, b S.
∈
• Associativity: a*(b*c) = (a*b)*c a ,b ,c belongs to S.
∀
• Identity Element: There exists e S such that a*e = e*a
∈
= a a S
∀ ∈
• Inverses: a S there exists a
∀ ∈ -1
S such that a*a
∈ -1
= a-
1
*a = e
• Commutative: a*b = b*a for all a, b S
∈

9. Must Satisfy Properties
Algebraic Structure Closure
Semi Group Closure, Associative
Monoid Closure, Associative, Identity
Group Closure, Associative, Identity, Inverse
Abelian Group Closure, Associative, Identity, Inverse,
Commutative

10. • Here a Table with different non empty set and operation
• N=Set of Natural Number
• Z=Set of Integer
• R=Set of Real Number
• E=Set of Even Number
• O=Set of Odd Number
• M=Set of Matrix
• +,-,×,÷ are the operations.

11. Set,
Operation
Algebraic
Structure
Semi
Group
Monoid Group
Abelian
Group
N,+ Y Y X X X
N,- X X X X X
N,× Y Y Y X X
N,÷ X X X X X
Z,+ Y Y Y Y Y
Z,- Y X X X X

12. Z,× Y Y Y X X
Z,÷ X X X X X
R,+ Y Y Y Y Y
R,- Y X X X X
R,× Y Y Y X X
R,÷ X X X X X
E,+ Y Y Y Y Y
M,+ Y Y Y Y Y
M,× Y Y Y X X
Set,
Operation
Algebraic
Structure
Semi
Group
Monoid Group
Abelian
Group

13. PROBLEMS
1. Show that the set of integer forms an abelian group
under addition.
2. Show that the cube root of unity is an abelian group
under multiplication.
3. G is the set of rational except -1 binary operation * is
defined as a*b= a+b+ab show that it is a group.
4. In Z we define a*b= a+b+1 show that (Z,*) is an abelian
group.
5. G is the set of all positive rational number and binary
operation * is defined as a*b= ab/7. Prove that it is an
abelian group.

14. Solving Algebraic Structures Problems by Composition Table
• Problem-1:
Set G = { 1, ω, ω2
} i.e., three roots of unity and form a
finite abelian group with respect to multiplication, also
prove this statement by composition table.
• Explanation :
Given, Set=G={1, ω, ω2
} , operation=‘*’ i.e.
multiplication.
• To prove that three roots of unity form a finite abelian
group we must satisfy the following five properties that is
Closure Property, Associative Property, Identity Property,
Inverse Property, and Commutative Property.
• Note-: ω3
=1

15. • 1) Closure Property –
• ∀ a , b G a * b G a=1 , b=
∈ ⇒ ∈ ω ∈ G 1 * (
⇒ ω ) = ω =
ω ∈ G Hence, Closure Property is satisfied.
• 2) Associative Property –
• (a* b) * c = a*(b *c) a , b , c G Let a=1, b=ω and
∀ ∈
c=ω2 So, LHS = ( a * b )*c = (1* ω ) *ω2
= ω3
=1
• RHS = a * ( b * c) = 1*( ω* ω2
) = ω3
= 1
• Hence, RHS = LHS Associative Property is also Satisfied
• 3) Identity Property –
• a *e = a a G e=identity=1 (in case of multiplication) 1
∀ ∈
G Let a=1*1= 1
∈
• 1 G Identity property is also satisfied.
∈

16. • 4) Inverse Property –
Here we can see that inverse of 1 is 1, inverse of ω is ω2
and inverse of ω2 is ω . These inverse belong to set G.
So, Inverse property is also satisfied.

17. 5) Commutative Property –
• a * b = b * a a , b G
∀ ∈
• Let a=1, b=ω
• LHS = a * b
• = 1*ω = ω
• RHS = b * a
• = ω *1= ω
• LSH=RHS
• Commutative Property is also satisfied.
• We can see that all five property is satisfied. Hence, Three roots
of unity form a finite abelian group with operation multiplication.
•

18. Forming Composition Table :
• Step-1:
Write all elements of set in row and column and given
operation ( * ) on the corner and multiply the elements of
the column with row element one by one and write it in the
row as shown in the figure given below.

19. • Step-2:
After multiplying each element of column with row
elements our composition table will look like figure given
below,

20. • Step-3:
We know that,
• ω3
=1 So, ω4
=ω3
.ω=1.ω=ω so our composition table
becomes

21. • Step-4:
Finding inverse of elements.
• Draw horizontal and vertical line from identity elements in
each row, the vertical line provides the inverse of row
elements, we can clearly see that inverse of 1 is 1,
inverse of ω is ω2 and inverse of ω2 is ω.

22. • Step-5:
Satisfying Properties of Abelian Group from Composition Table
• We see in the composition table all numbers are in set G, Hence
Closure Property is satisfied.
• We see that all numbers in composition table belong to set G,
Hence Associative Property is satisfied.
• In composition table in each row there is identity element 1,
Identity Property is satisfied.
• We see that inverse of 1 is 1, inverse of ω is ω2
and inverse of
ω2
is ω. All belongs to set G, hence Inverse Property is also
satisfied.
• All numbers in composition table belongs to set G , Commutative
Property is also satisfied.
• Hence, G = { 1, ω, ω2
} is an abelian group with respect to
multiplication.

23. • Problem-2:
Set G = { 1, -1 , i , -i } i.e., four roots of unity and form a
finite abelian group with respect to multiplication.