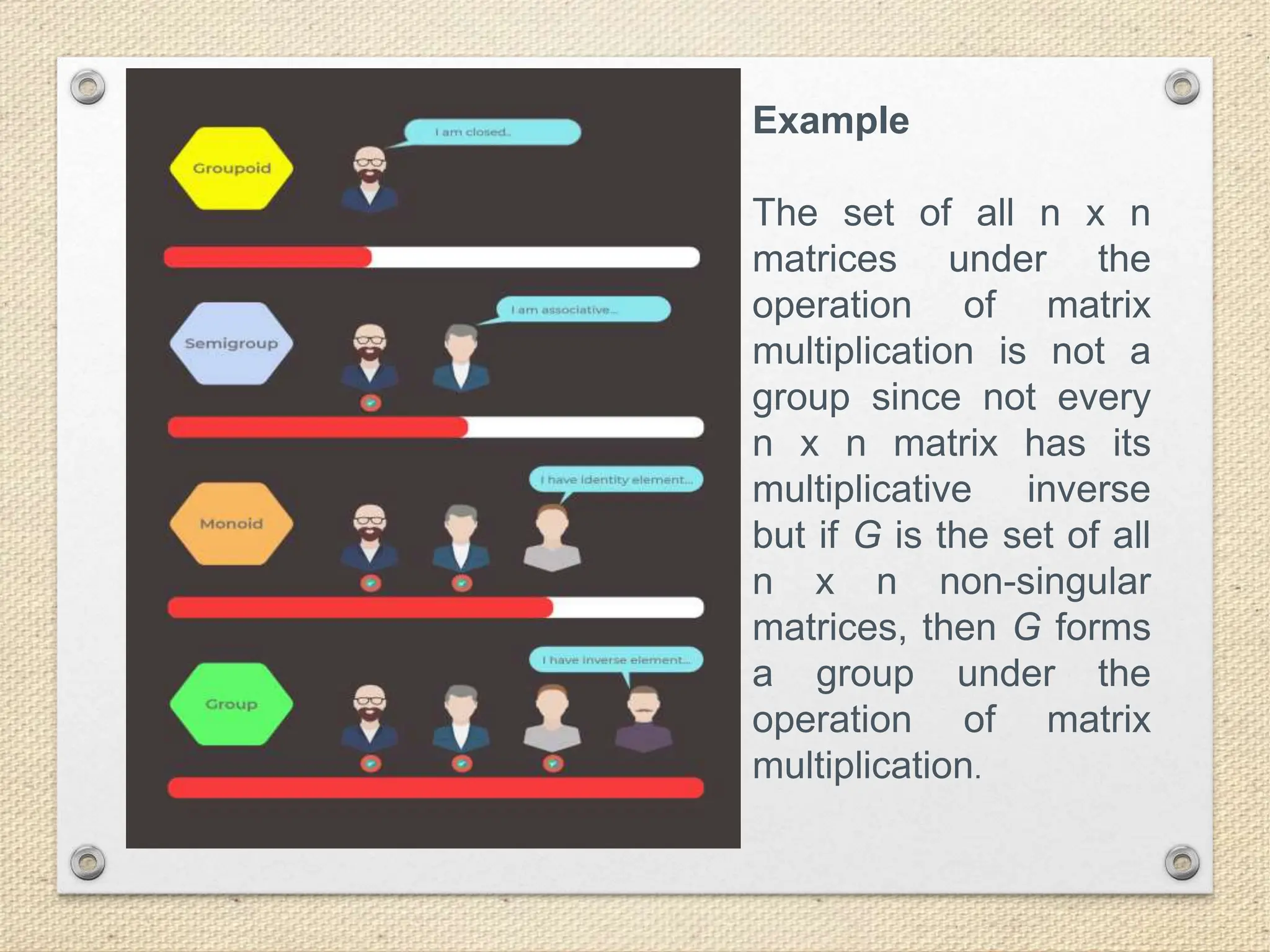
A group in abstract algebra is defined as a set of elements equipped with a binary operation that satisfies closure, associativity, identity, and inverses. The document elaborates on group properties, such as the distinction between abelian and non-abelian groups, and provides examples of closure and inverse properties in various mathematical contexts. Additionally, it discusses the concept of subgroups and the particular case of finite abelian groups, highlighting their group characteristics.

1. Abstract Algebra

2. Definition of a Group
A Group G is a collection of elements
together with a binary operation* which
satisfies the following properties:
Closure
Associativity
Identity
Inverses
* A binary operation is a function on G
which assigns an element of G to each
ordered pair of elements in G. For
example, multiplication and addition are
binary operations.
rubic cube permutation group
http://en.wikipedia.org/wiki/Permutation_group

3. Properties of a Group:
Closure [groupoid]
Example:
The Integers under Addition, (Z, +)
1 and 2 are elements of Z,
1+2 = 3, also an element of Z
Non-Examples:
The Odd Integers are not closed under
Addition. For example, 3 and 5 are odd
integers, but 3+5 = 8 and 8 is not an odd
integer.
The Integers lack inverses under
Multiplication, as do the Rational numbers
(because of 0.) However, if we remove 0 from
the Rational numbers, we obtain an infinite
closed group under multiplication.
“If we combine any two elements in the group under the binary
operation, the result is always another element in the group.” -- Geoff
"members only"
http://en.wikipedia.org/wiki/index.html?curid=12686
870

4. Properties of a Group:
Associativity [semigroup]
The Associative Property, familiar from
ordinary arithmetic on real numbers,
states that (ab)c = a(bc). This may be
extended to as many elements as
necessary.
For example:
In Integers,
a+(b+c) = (a+b)+c.
In Matrix Multiplication,
(A*B)*C=A*(B*C).
In function composition,
f*(g*h) = (f*g)*h.
This is a property of all groups.
Caution:
The Commutative Property, also familiar
from ordinary arithmetic on real numbers,
does not generally apply to all groups!
Only Abelian groups are commutative.
associative loop
http://en.wikipedia.org/wiki/List_of_algebraic_structures

5. Properties of a Group:
Identity [monoid]
The Identity Property, familiar from
ordinary arithmetic on real numbers,
states that, for all elements a in G,
a+e = e+a = a.
For example,
in Integers, a+0 = 0+a = a.
In (Q*, X), a*1 = 1*a = a.
In Matrix Multiplication, A*I = I*A = A.
This is a property of all groups.
The Identity is Unique!
There is only one identity
element in any group.
This property is used in
proofs.
|1 0|
|0 1|
= I

6. Properties of a Group:
Inverses
The inverse of an element, combined with that element, gives the identity.
Inverses are unique. That is, each element has exactly one inverse, and no two
distinct elements have the same inverse.
The uniqueness of inverses is used in proofs.
For example...
In (Z,+), the inverse of x is -x.
In (Q*, X), the inverse of x is 1
/x.
In abstract algebra, the inverse of an element a is usually written a-1
.
This is why (GL,n) and (SL, n) do not include singular matrices; only nonsingular
matrices have inverses.
In Zn, the modular integers, the group operation is understood to be addition, because
if n is not prime, multiplicative inverses do not exist, or are not unique.
The U(n) groups are finite groups under modular multiplication.

7. Example
The set of all n x n
matrices under the
operation of matrix
multiplication is not a
group since not every
n x n matrix has its
multiplicative inverse
but if G is the set of all
n x n non-singular
matrices, then G forms
a group under the
operation of matrix
multiplication.

8. Abelian Groups
Abelian Groups are groups which have the
Commutative property, a*b=b*a for all a and b in G.
This is so familiar from ordinary arithmetic on Real
numbers, that students who are new to Abstract
Algebra must be careful not to assume that it
applies to the group on hand.
Abelian groups are named after Neils Abel, a
Norwegian mathematician.
Abelian groups may be recognized
by a diagonal symmetry in their
Cayley table (a table showing the
group elements and the results of
their composition under the group
binary operation.)
This symmetry may be used in
constructing a Cayley table, if we
know that the group is Abelian.
Neils Abel postage stamp http://en.wikipedia.org/wiki/Neils_Abel
Cayley tables for Z4 and U8
http://www.math.sunysb.edu/~joa/MAT313/hw-VIII---313.html

9. Subgroups
A subgroup H of a group G is a subset of G together
with the group operation, such that H is also a group.
1. A semi group satisfies associative
2. A monoid is a semi group with an identity elements
3. A group is a monoid with Inverse property.
4. An Abelian group is a group with commutative
property.
5. A sub group inherits all the properties of group.
euler portrait
http://www.math.o
hio-
state.edu/~sinnott/
ReadingClassics/h
omepage.html

10. Consider binary relation * defined
on set A={A,B,C,D} by following
table and check commutative and
Associative
euler portrait
http://www.math.o
hio-
state.edu/~sinnott/
ReadingClassics/h
omepage.html
* A B C D
A A C B D
B D A B C
C C D A A
D D B A C
Commutative
Associative

11. Prove the set ß={0,1,2,3,4} is a
finite abelian group of order 5
under addition
euler portrait
http://www.math.o
hio-
state.edu/~sinnott/
ReadingClassics/h
omepage.html
+5 0 1 2 3 4
0
1
2
3
4
Closure Property
Associative Property
Addition is an associative operation, and this property holds
for all elements in β.
Identity Property
The element 0 is the identity element because, for all a in β, 0
+ a = a + 0 = a. This fulfills the requirement for an identity
element.
Inverse Property
Commutative Property
0 + 0 = 0
0 + 1 = 1
0 + 2 = 2
0 + 3 = 3
0 + 4 = 4
1 + 1 = 2
1 + 2 = 3
1 + 3 = 4
1 + 4 = 0
2 + 2 = 4
2 + 3 = 0
2 + 4 = 1
3 + 3 = 1
3 + 4 = 2
4 + 4 = 3
•For 0, its inverse is 0.
•For 1, its inverse is 4 (1 + 4 = 4 + 1 = 0).
•For 2, its inverse is 3 (2 + 3 = 3 + 2 = 0).
•For 3, its inverse is 2 (3 + 2 = 2 + 3 = 0).
•For 4, its inverse is 1 (4 + 1 = 1 + 4 = 0).

12. Prove the set ß={0,1,2,3,4} is a
finite abelian group of order 5
under addition
euler portrait
http://www.math.o
hio-
state.edu/~sinnott/
ReadingClassics/h
omepage.html
+5 0 1 2 3 4
0
1
2
3
4
Closure Property
Associative Property
Identity Property
Inverse Property
Commutative Property

13. Let Z={1,2,..n-1} let
euler portrait
http://www.math.o
hio-
state.edu/~sinnott/
ReadingClassics/h
omepage.html
*7 1 2 3 4 5 6
1
2
3
4
5
6
Closure Property
Associative Property
Identity Property
Inverse Property
Commutative Property