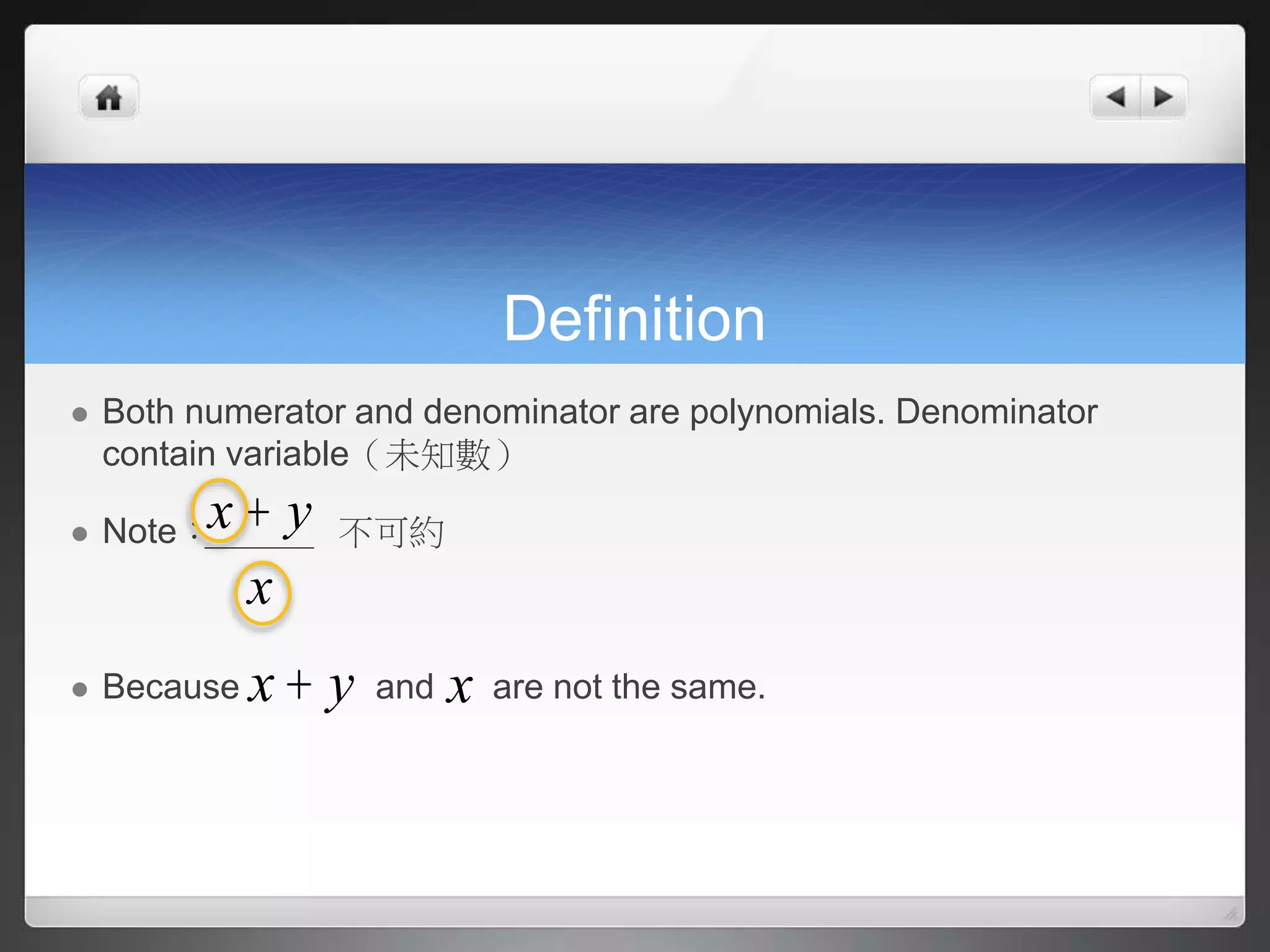
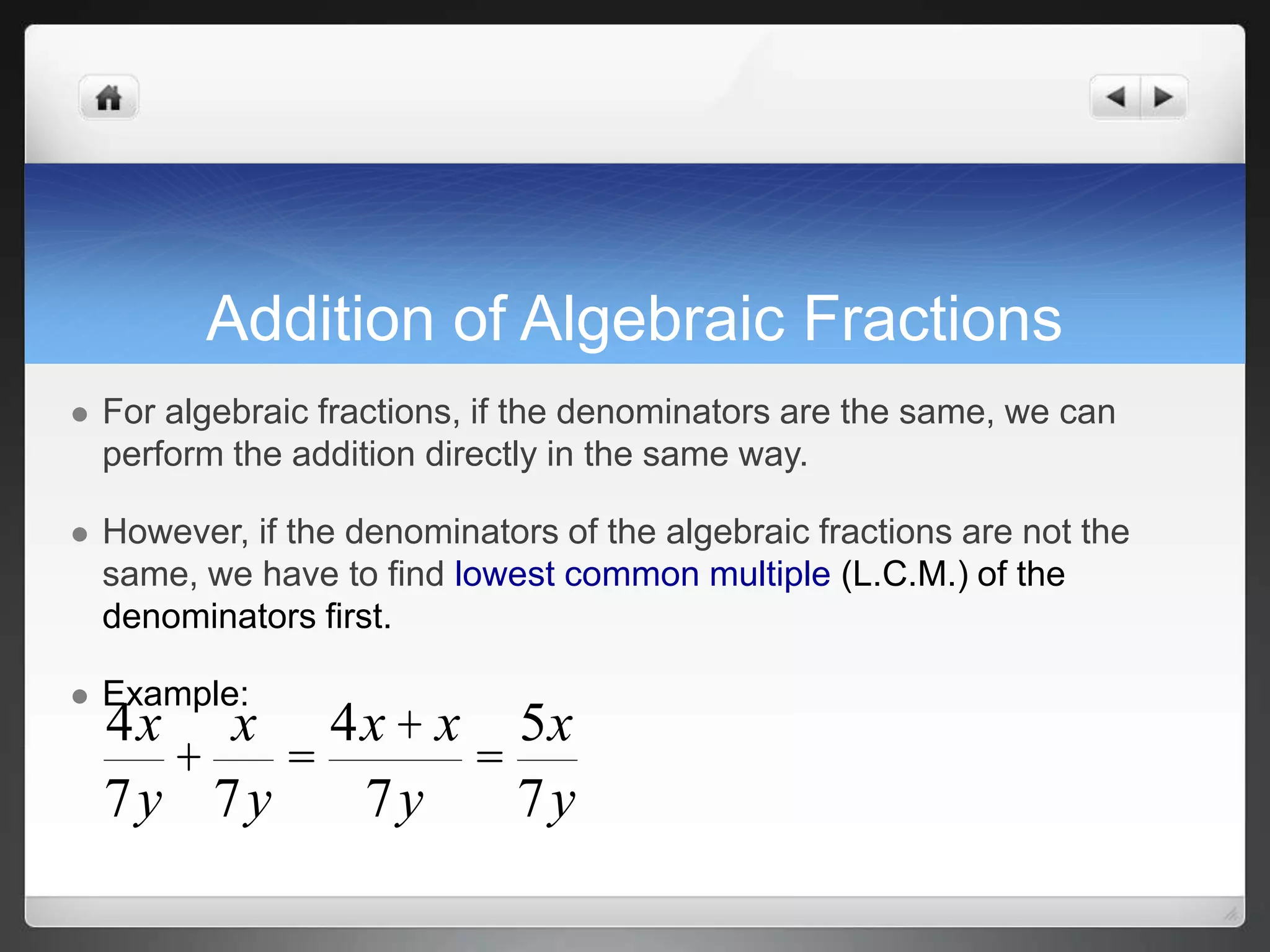
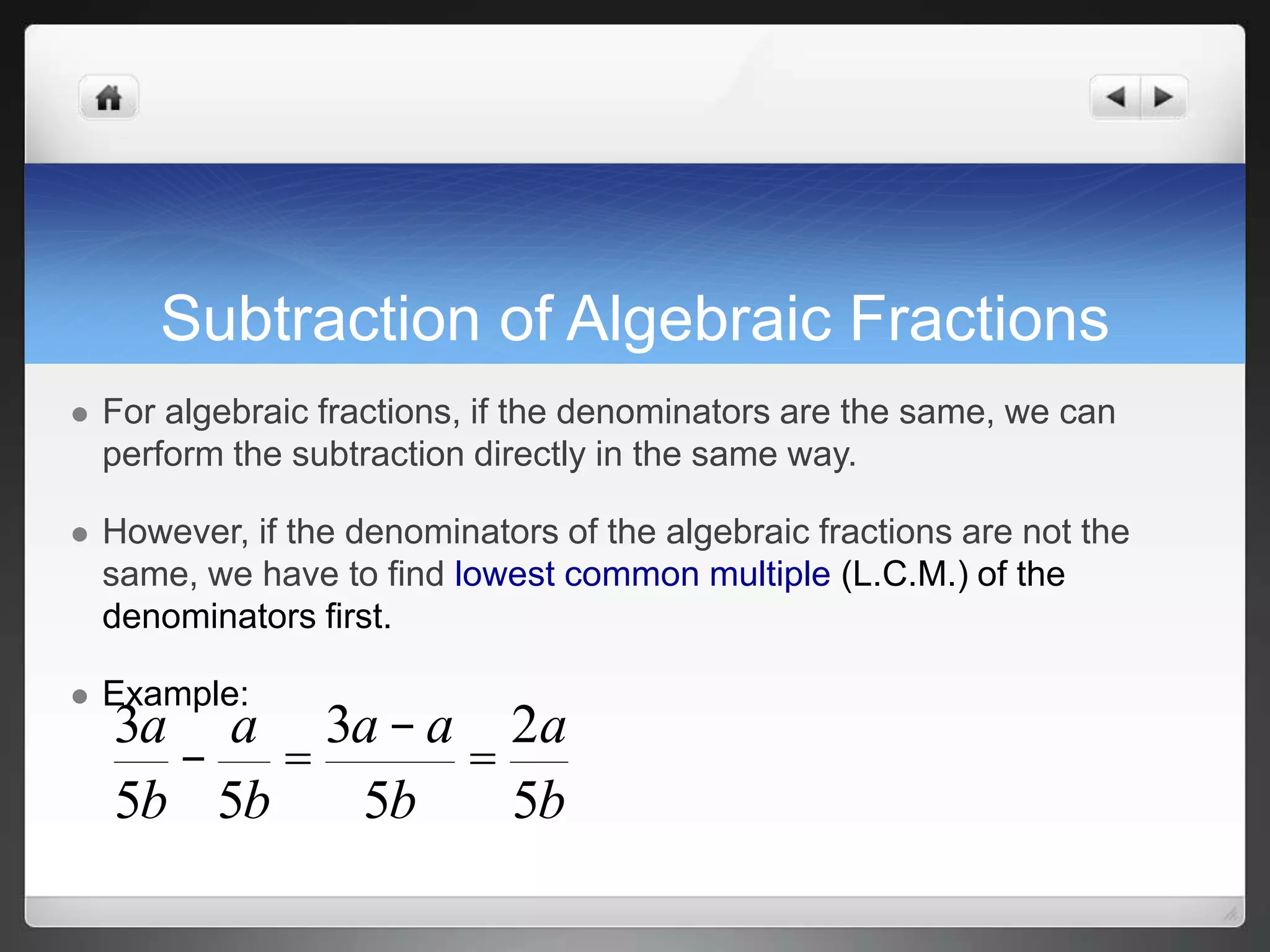
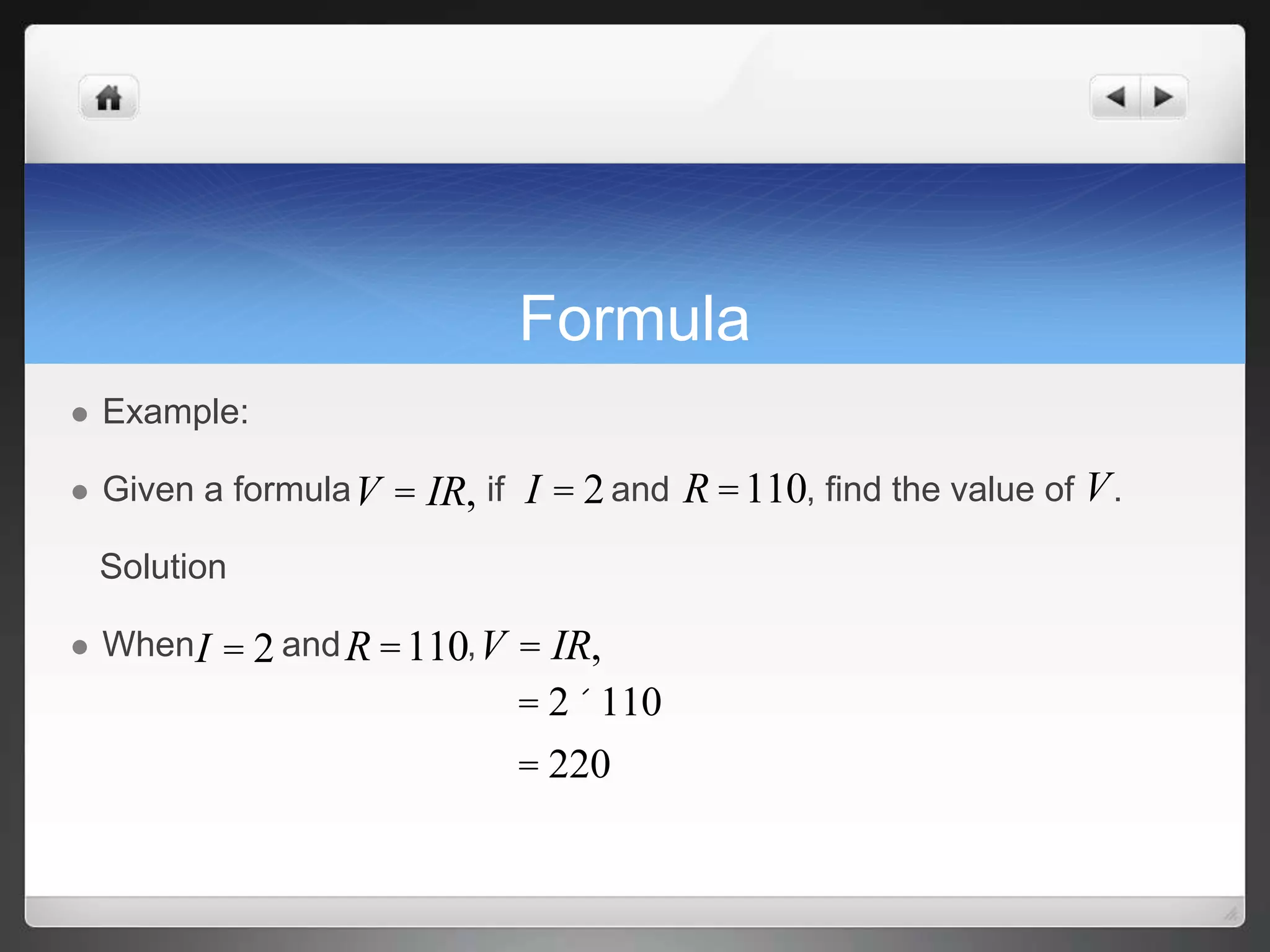
This document discusses algebraic fractions including: 1) Definitions of algebraic fractions where both the numerator and denominator are polynomials. 2) Methods for multiplying, dividing, adding, and subtracting algebraic fractions by treating them similar to regular fractions but using the lowest common multiple of denominators when needed. 3) Examples of using formulas to solve for unknown variables by substituting given values into the formula.

1. Chapter 3
Algebraic Fraction and
Formulars
組員：蔡敬霈（5）
羅力恆（6）
楊曉泓（8）
羅祖耀（9）
李啟駿（12）
梁啟章（13）

2. Definition
 Both numerator and denominator are polynomials. Denominator
contain variable（未知數）
x + y
x
x + y x
 Note： 不可約
 Because and are not the same.

3. Multiplication of Algebraic Fractions
 In multiplication of fractions, we
multiply the numerators and
denominators separately to get
the product.
 Example:3
5
´
7
4
=
3´7
5´ 4
=
21
20
 The same method can be
applied to the multiplication of
algebraic fractions.
 Example:
a
c
´
c
d
=
a ´ c
b´ d

4. Division of Algebraic Fractions
 The principle of division of algebraic fractions is the same as that of
fractions.
 Example:
a
b
¸
c
d
=
a
b
´
d
c
=
a ´ d
b´ c
=
ad
bc

5. Addition of Algebraic Fractions
 For algebraic fractions, if the denominators are the same, we can
perform the addition directly in the same way.
 However, if the denominators of the algebraic fractions are not the
same, we have to find lowest common multiple (L.C.M.) of the
denominators first.
 Example:
4x
+
7y
x
7y
=
4x + x
7y
=
5x
7y

6. Subtraction of Algebraic Fractions
 For algebraic fractions, if the denominators are the same, we can
perform the subtraction directly in the same way.
 However, if the denominators of the algebraic fractions are not the
same, we have to find lowest common multiple (L.C.M.) of the
denominators first.
 Example:
3a
-
5b
a
5b
=
3a - a
5b
=
2a
5b

7. Formula
h
b
A = BH
If B = 4, H = 6
A = BH
= 4 X 6 = 24
In fact, when the values of two
variables are given, the values of
the remaining variable is fixed and
can be found by substitution.

8. Formula
 Example:
V = IR, I = 2 R = 110 V
 Given a formula if and , find the value of .
Solution
I = 2 R =110 V = IR,
 When and ,
= 2´110
= 220

9. Change of Subject