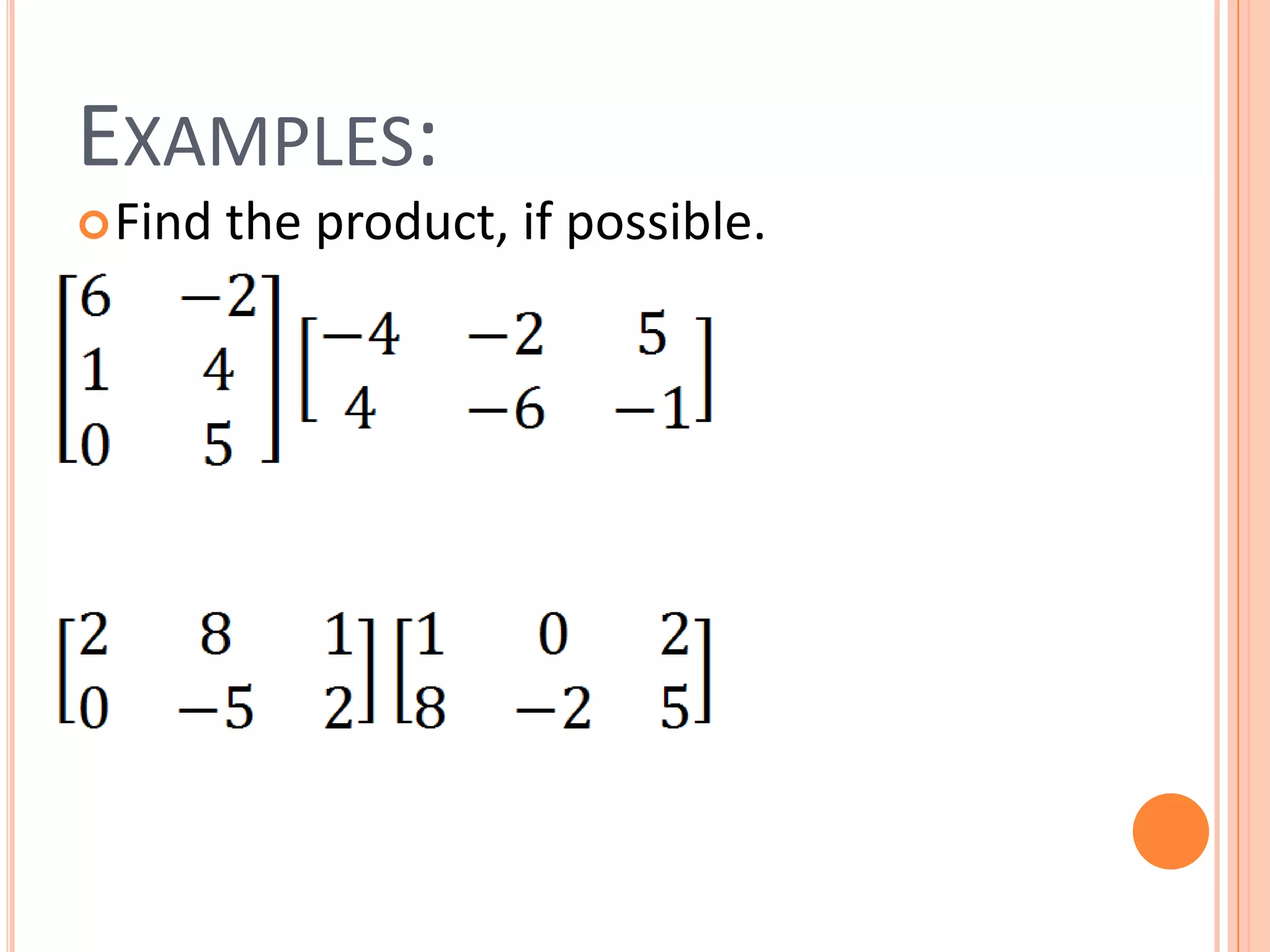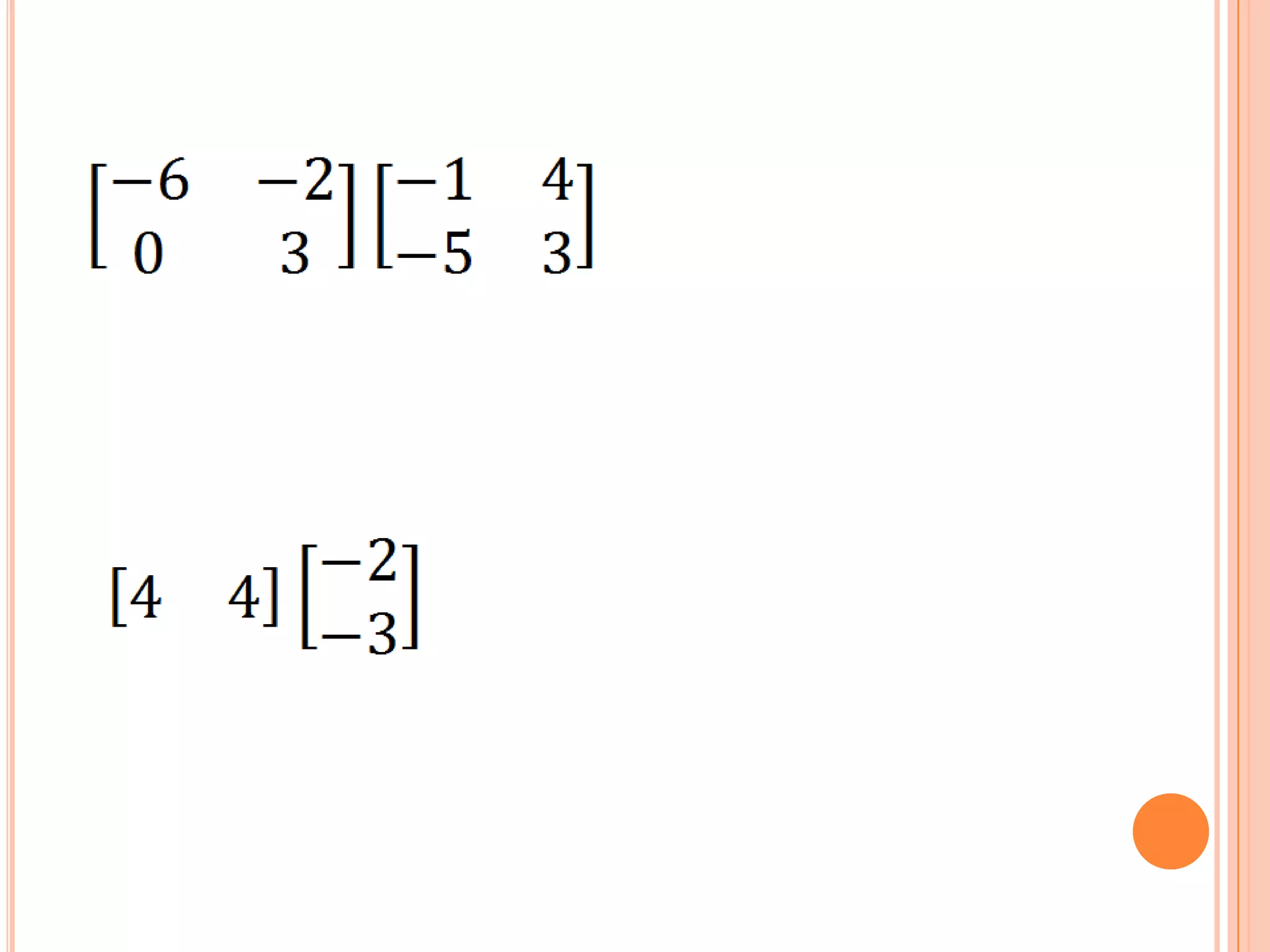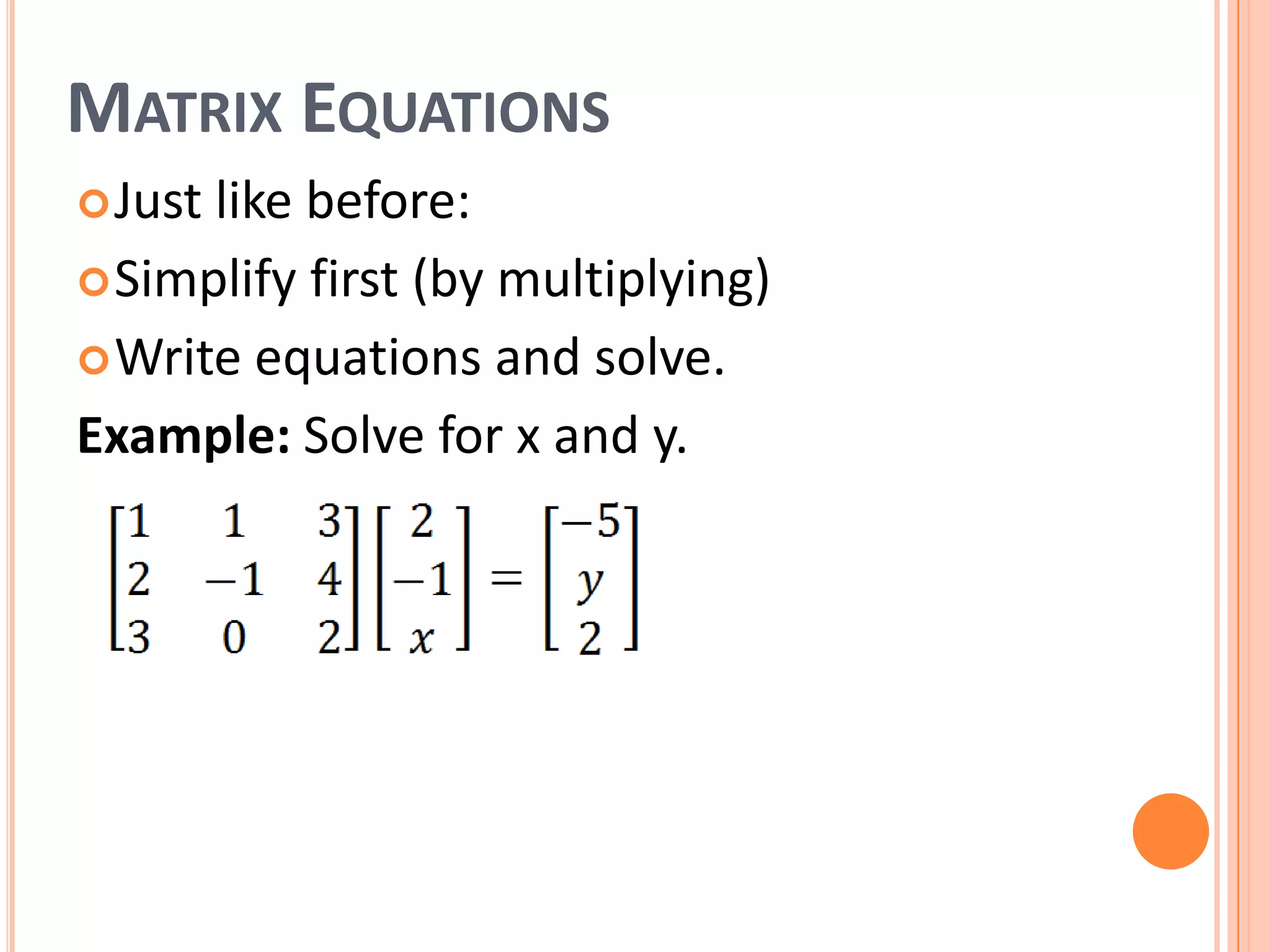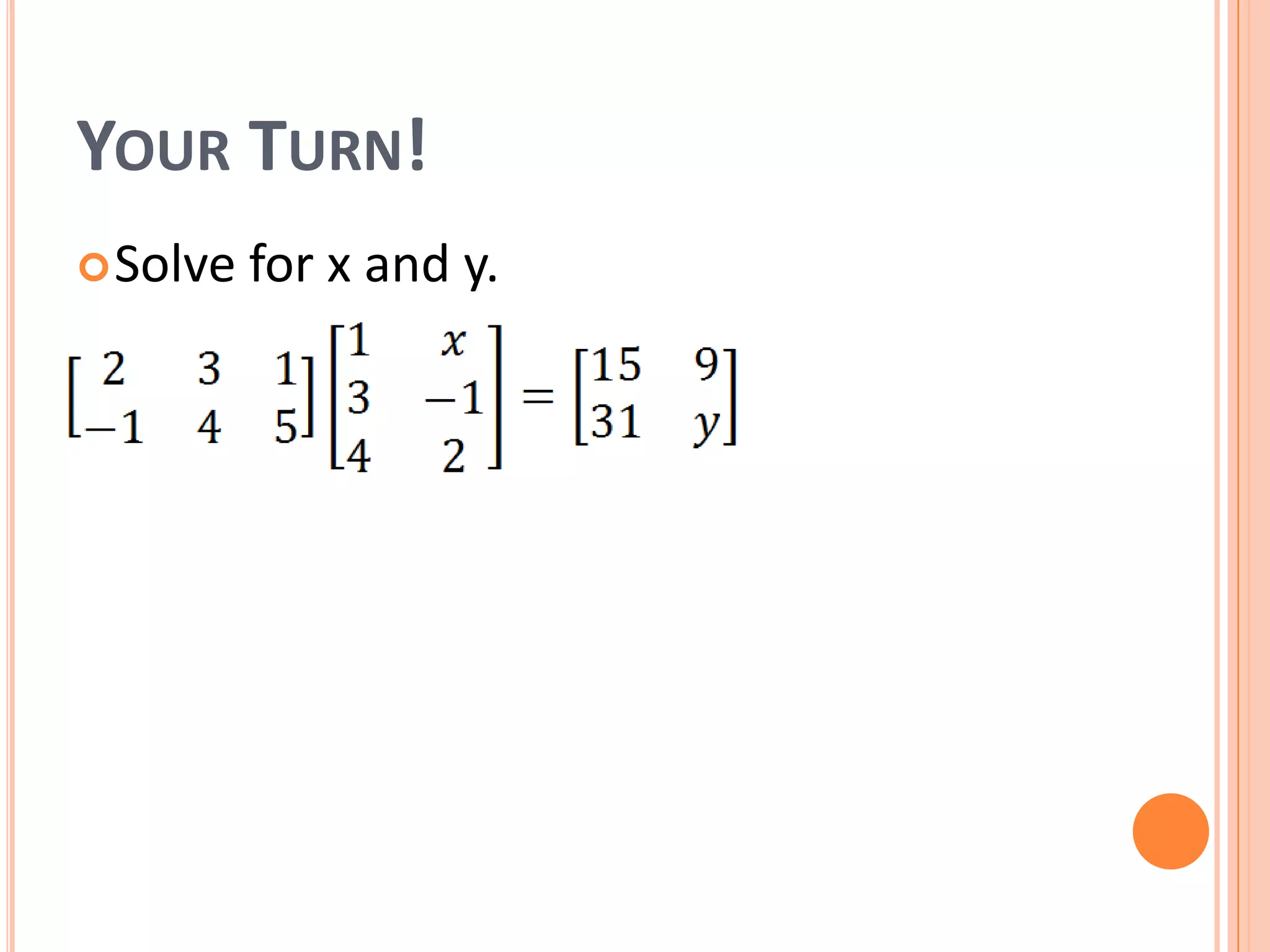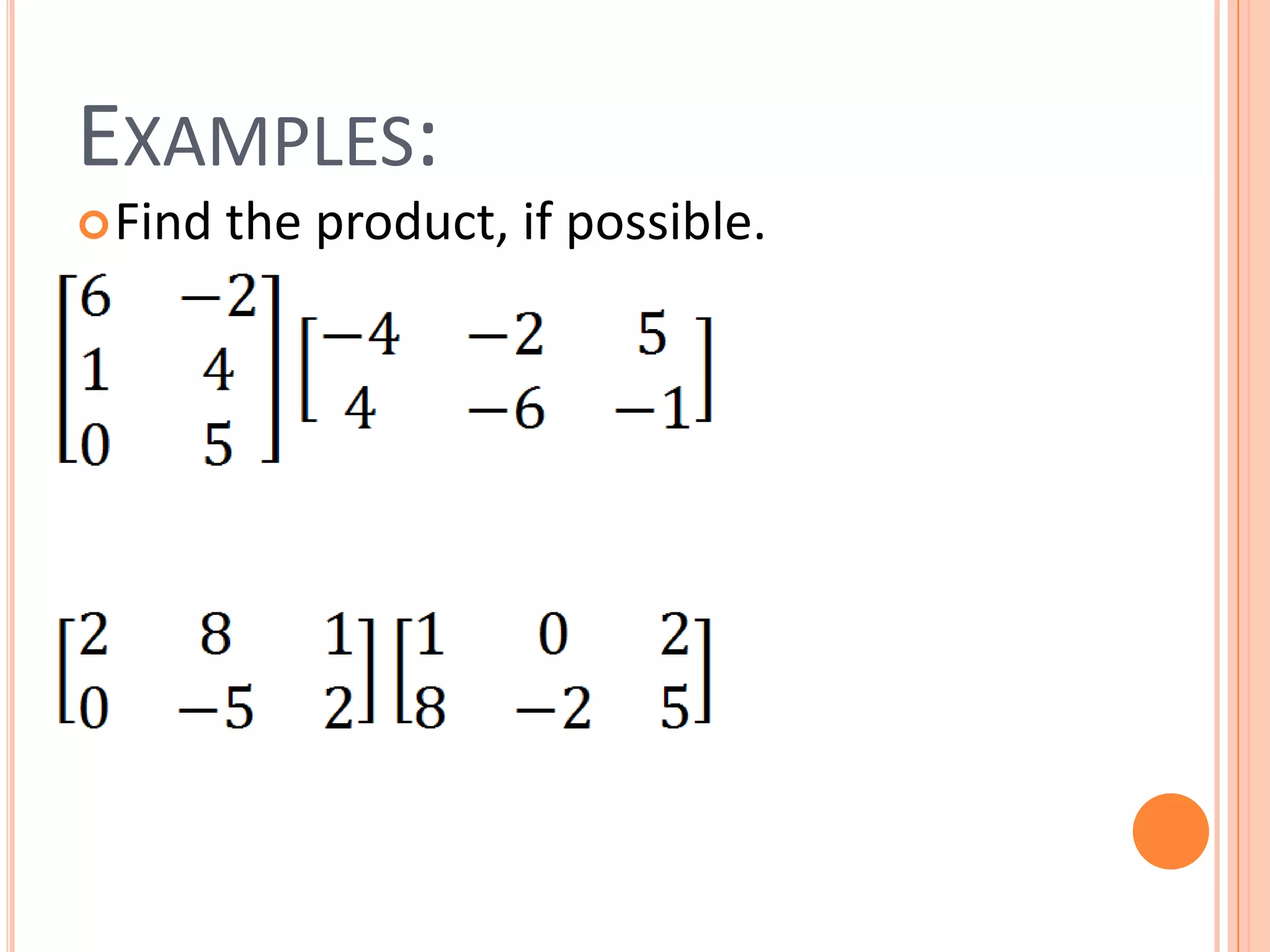
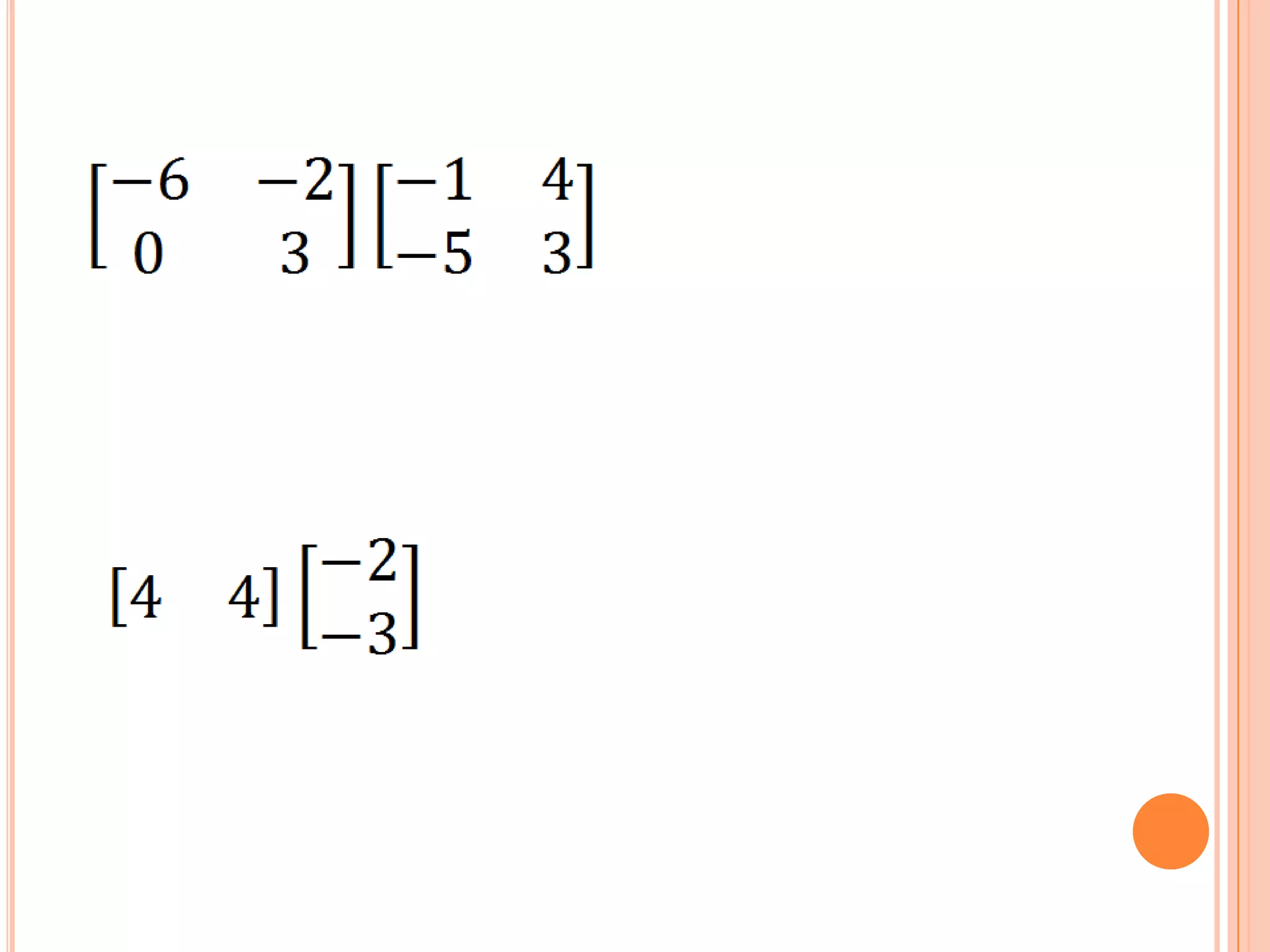
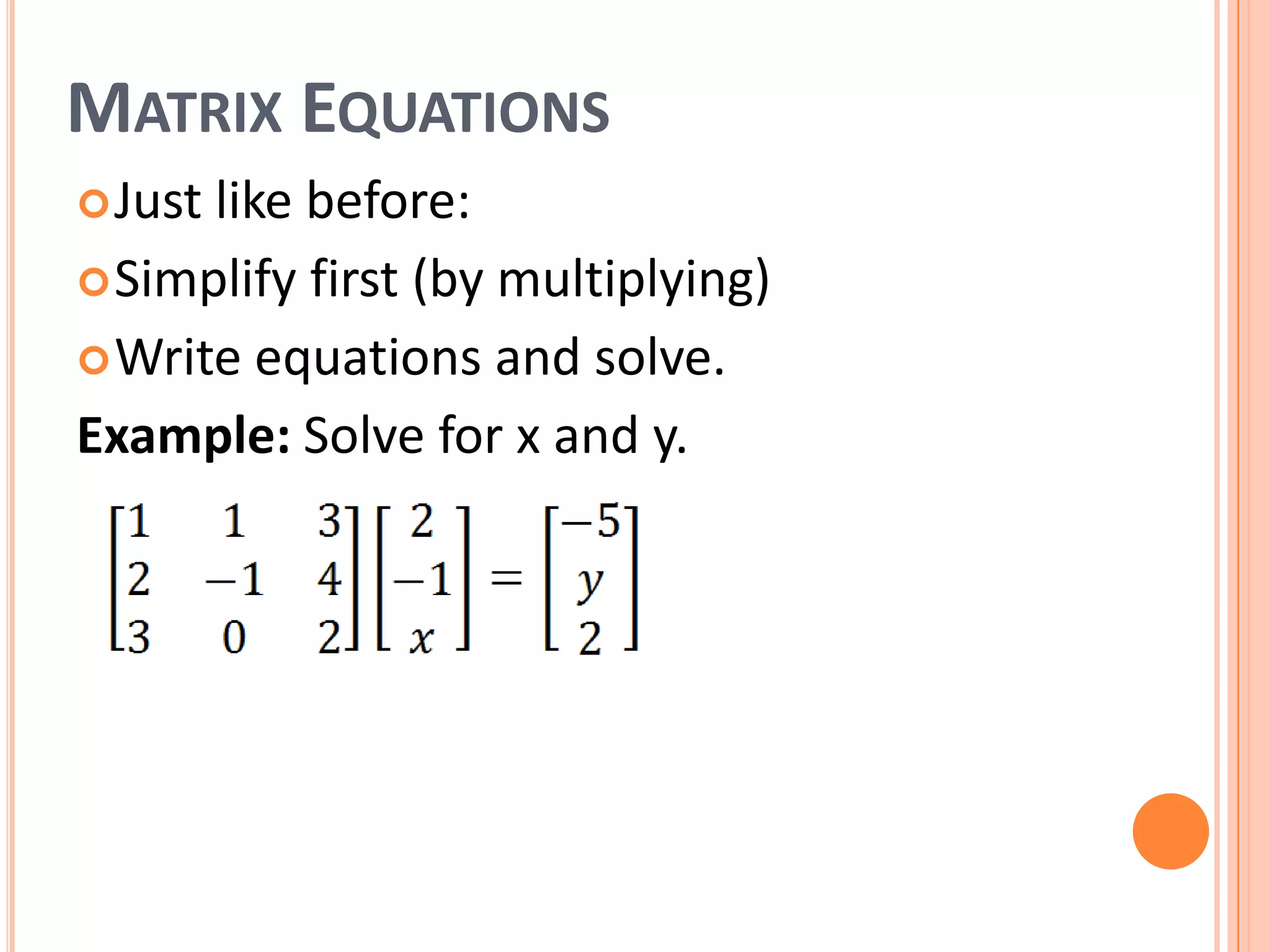
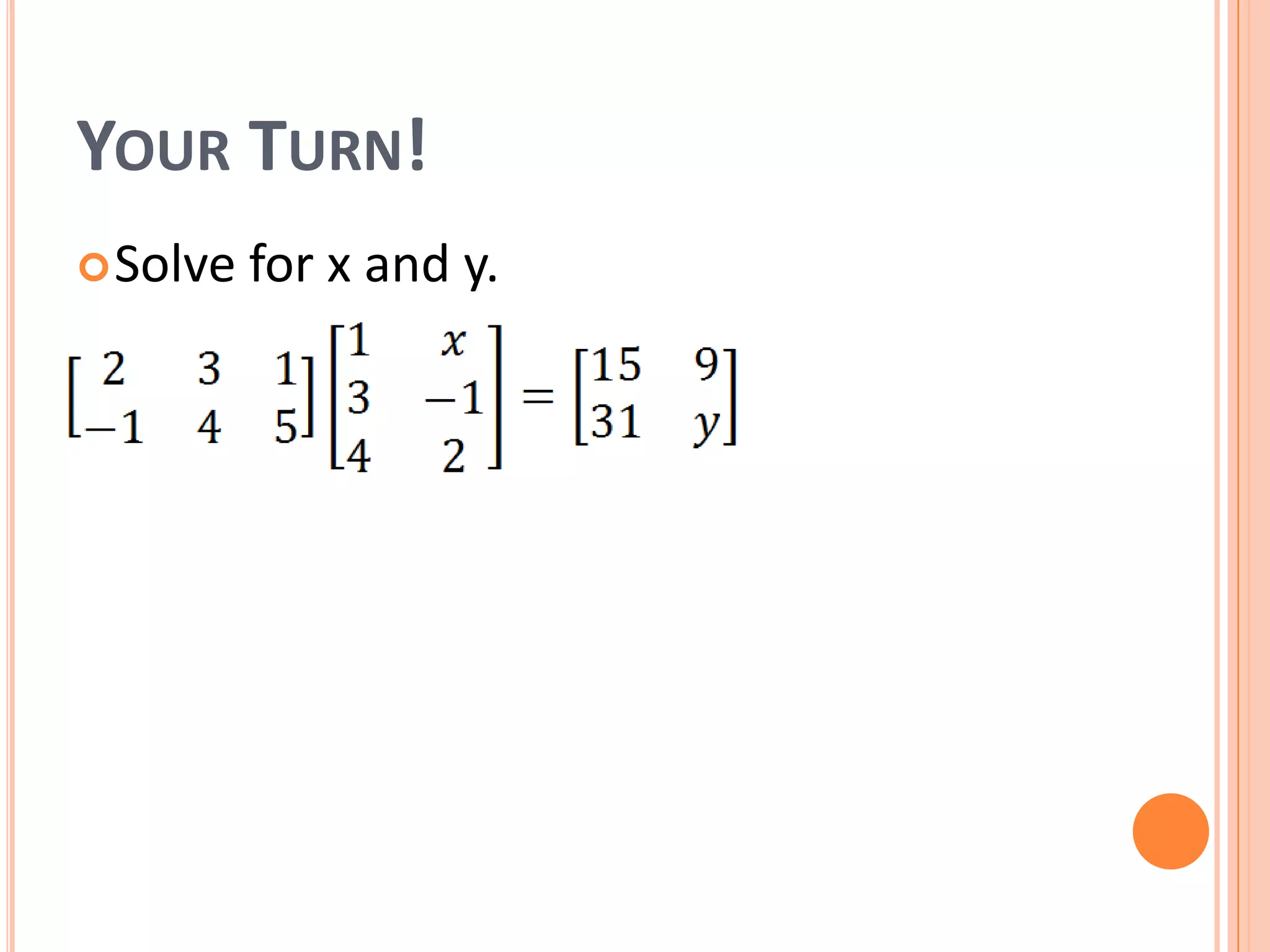
The document discusses multiplying matrices and describes that: 1) The number of columns in the first matrix must equal the rows of the second matrix for them to be multiplied. 2) The result of multiplying matrices A and B will be a matrix with the number of rows of A and columns of B. 3) To find each entry of the product matrix, multiply corresponding entries across rows of the first and down columns of the second and sum the results.

1. 4.2 MULTIPLYING MATRICES

2. DESCRIBING MATRIX PRODUCTS
To multiply matrices A and B, the # of
columns in A must match the # of rows in B
If A is m x n and B is n x p, AB will be m x p.
A ∙ B = AB
mxn nxp mxp
What will be the dimensions of AB if:
A is 2 x 3 and B is 3 x 4?
A is 3 x 2 and B is 3 x 4?

3. FINDING THE PRODUCT
For each entry in AB:
Multiply entries across the same row of A,
by those down the same column of B,
then add.
Example:

4. EXAMPLES:
 Find the product, if possible.

6. YOUR TURN!
Find AB if:

7. MATRIX MULTIPLICATION PROPERTIES:
Find AB if:
Now find BA.
Is matrix multiplication commutative?

8. MORE PROPERTIES:
Simplify each expression if:
1. A(B + C)
2. AB + AC
The distributive property is still true
for matrices!

9. YOUR TURN!
 Find B(A + C)

10. MATRIX EQUATIONS
 Justlike before:
 Simplify first (by multiplying)
 Write equations and solve.
Example: Solve for x and y.

11. YOUR TURN!
 Solve for x and y.