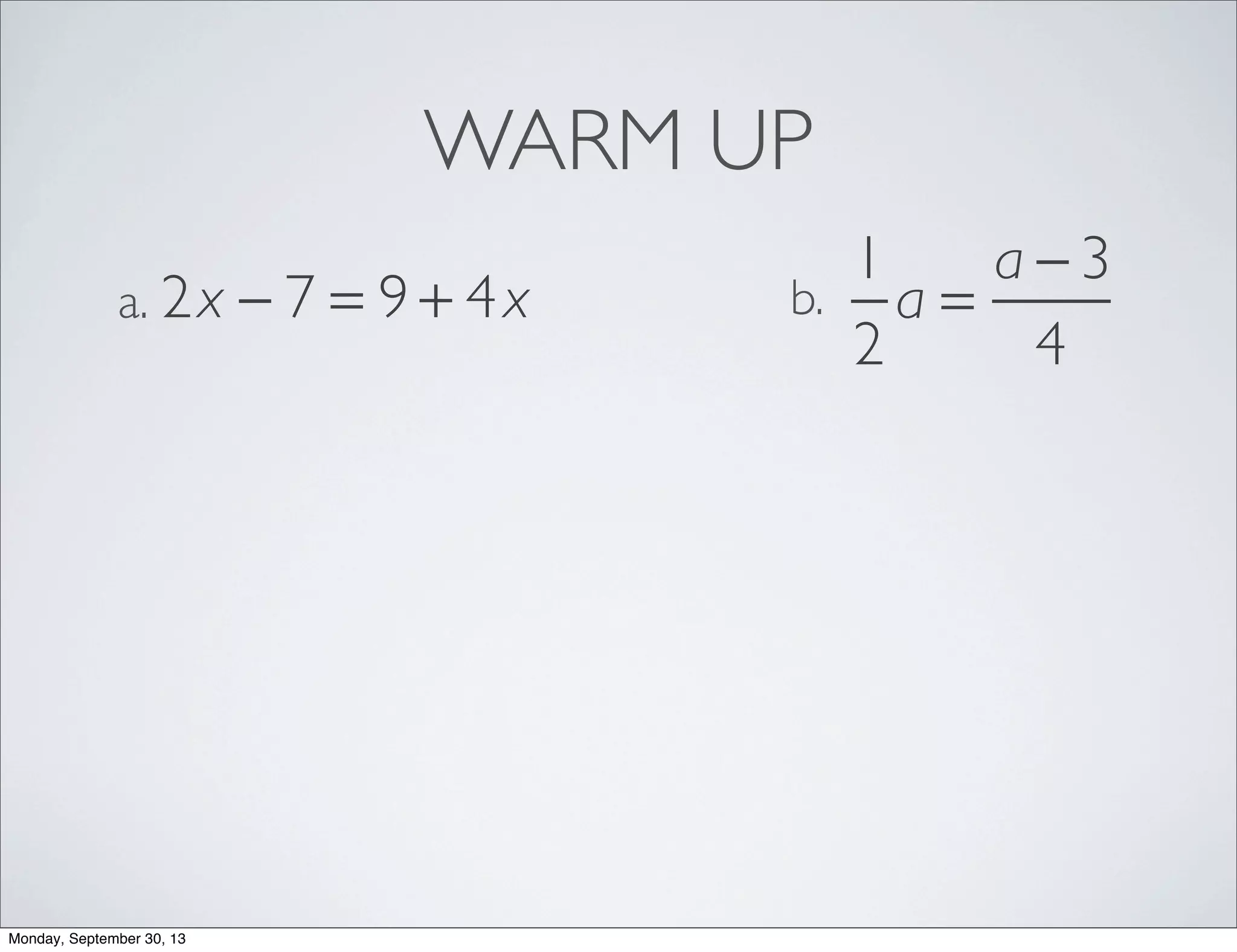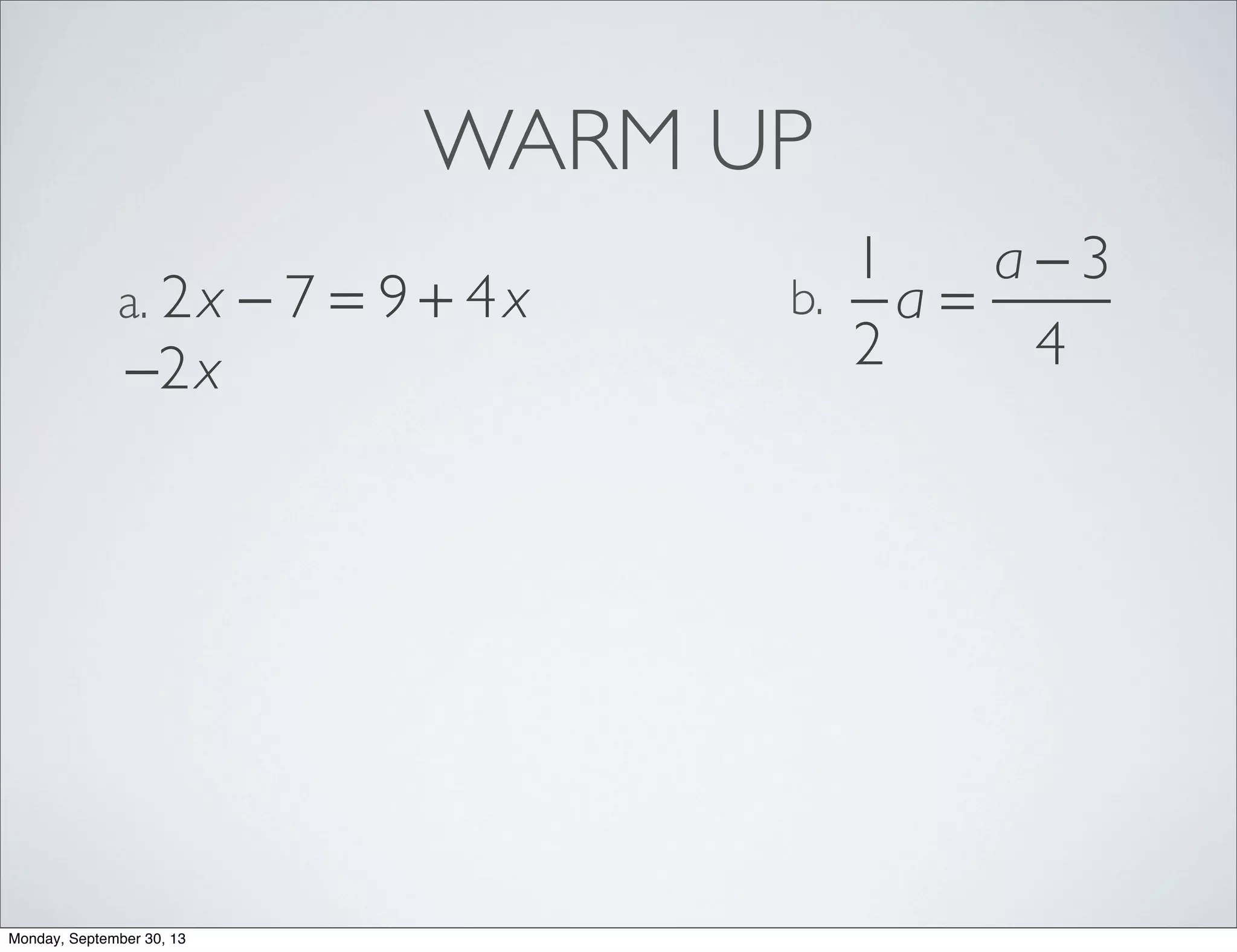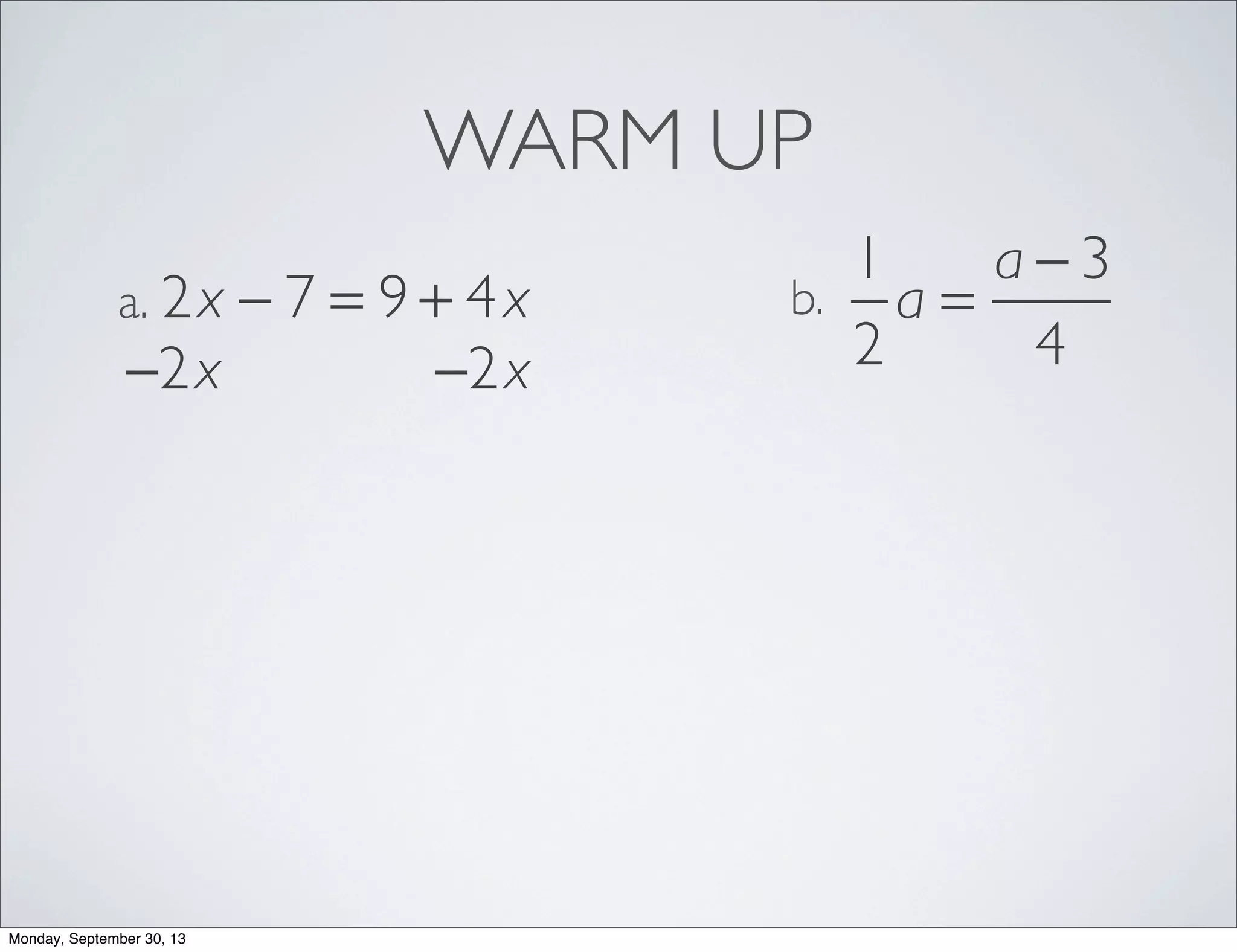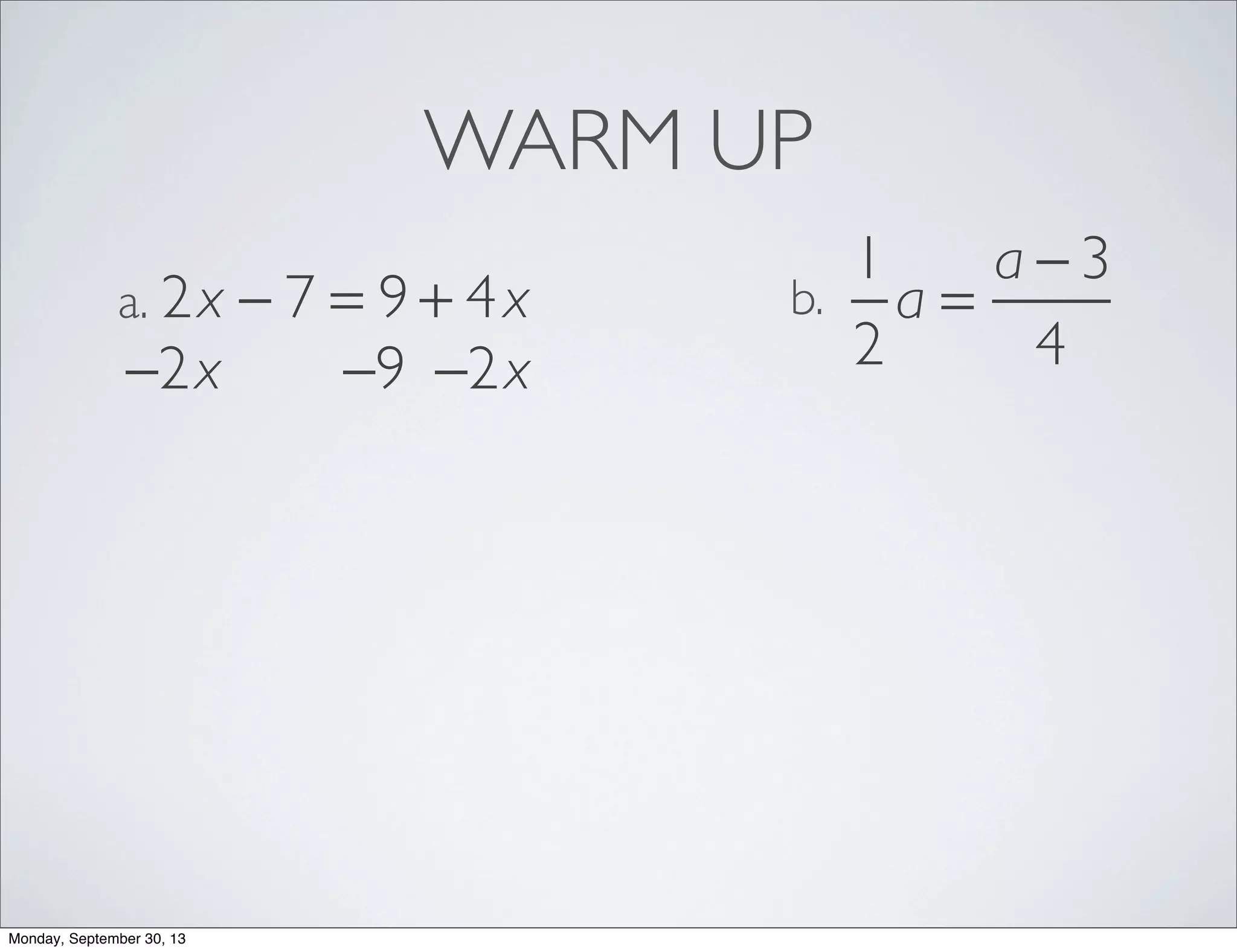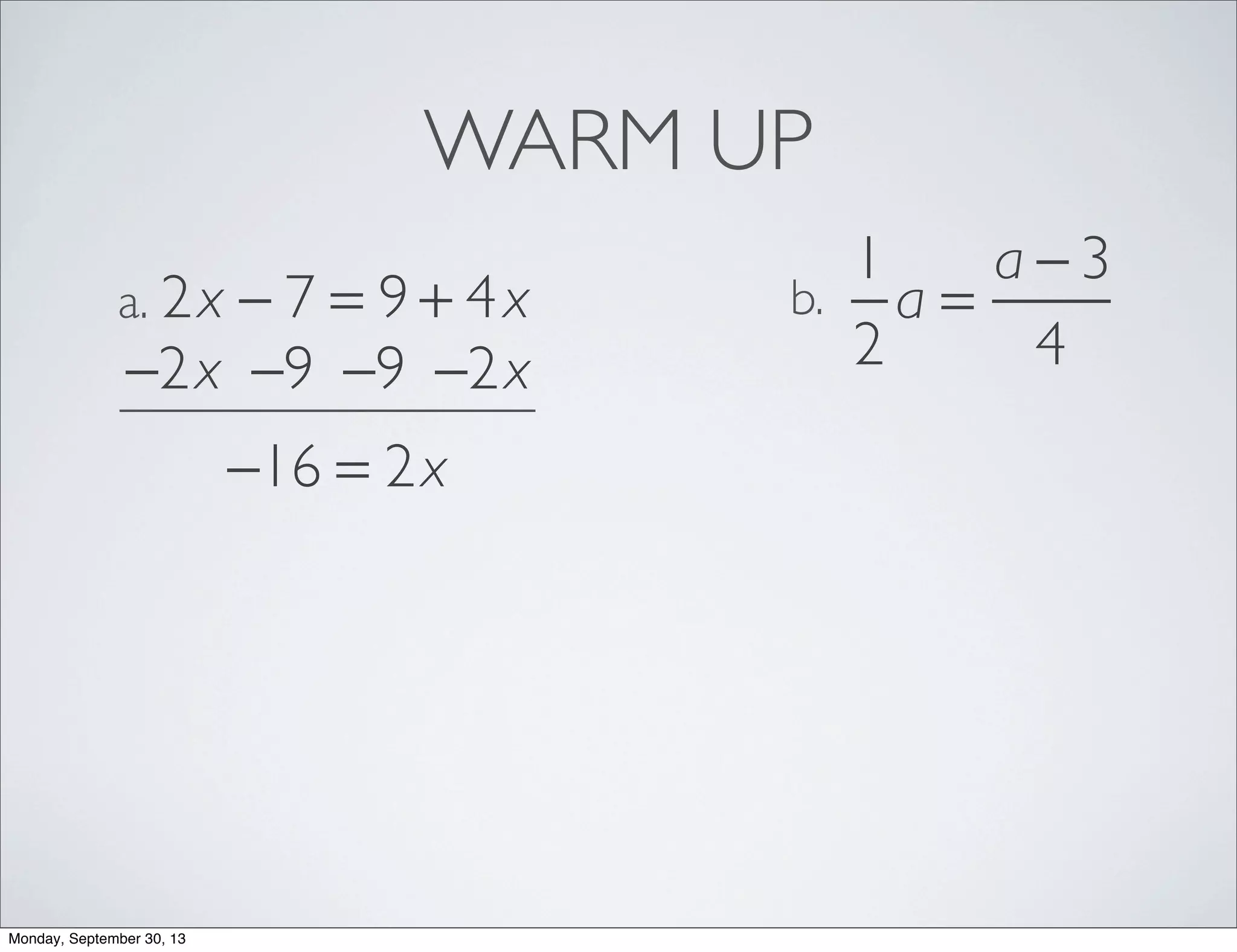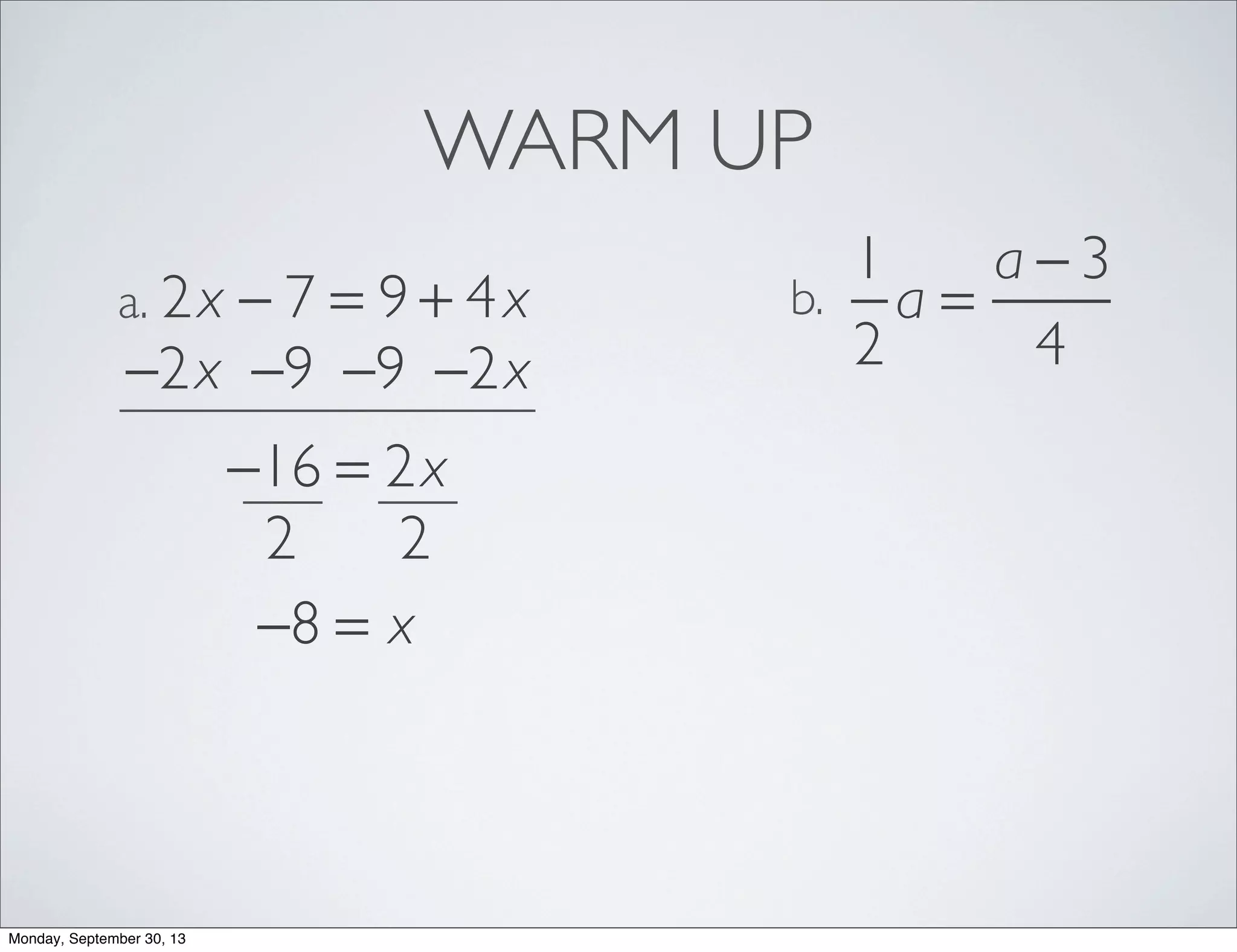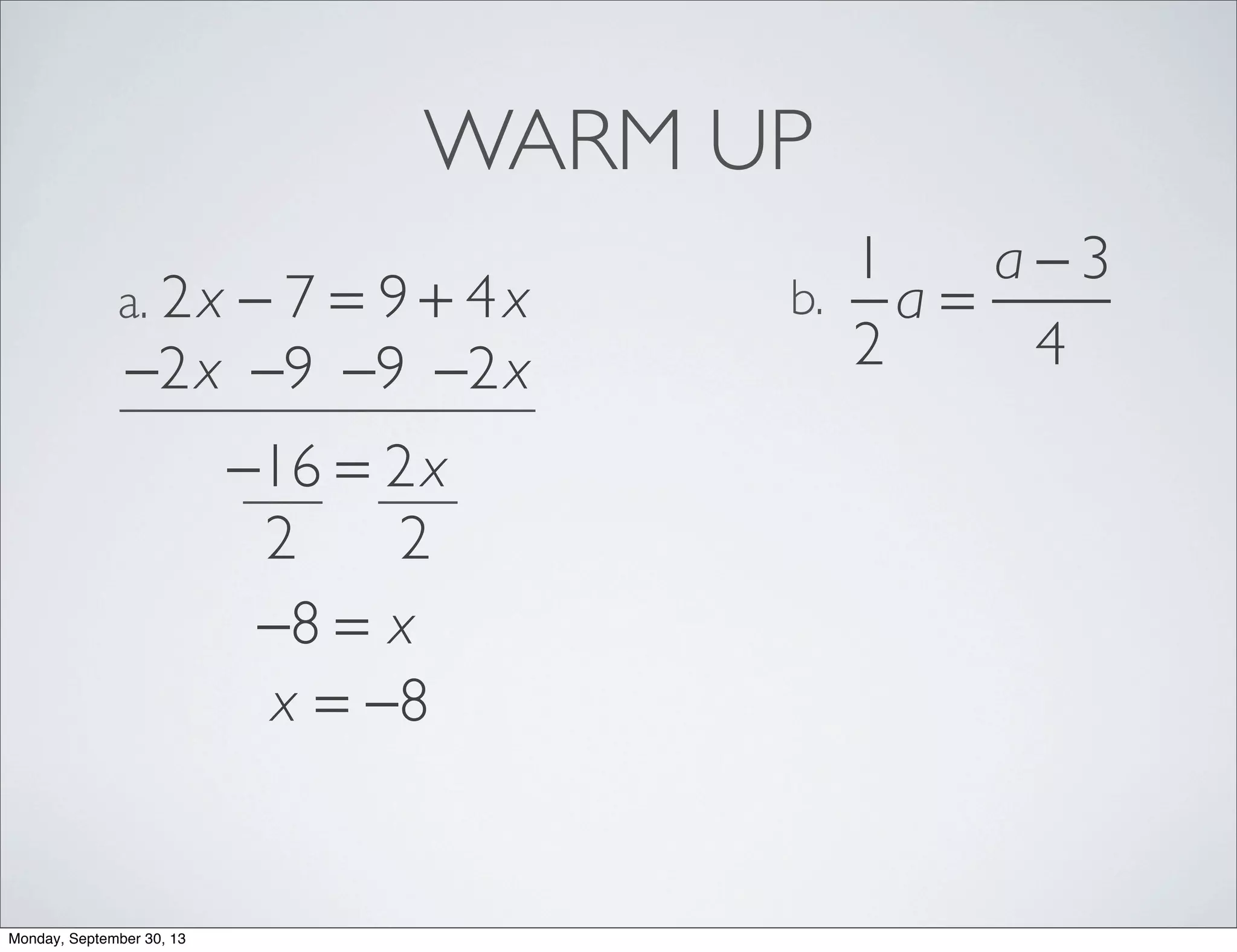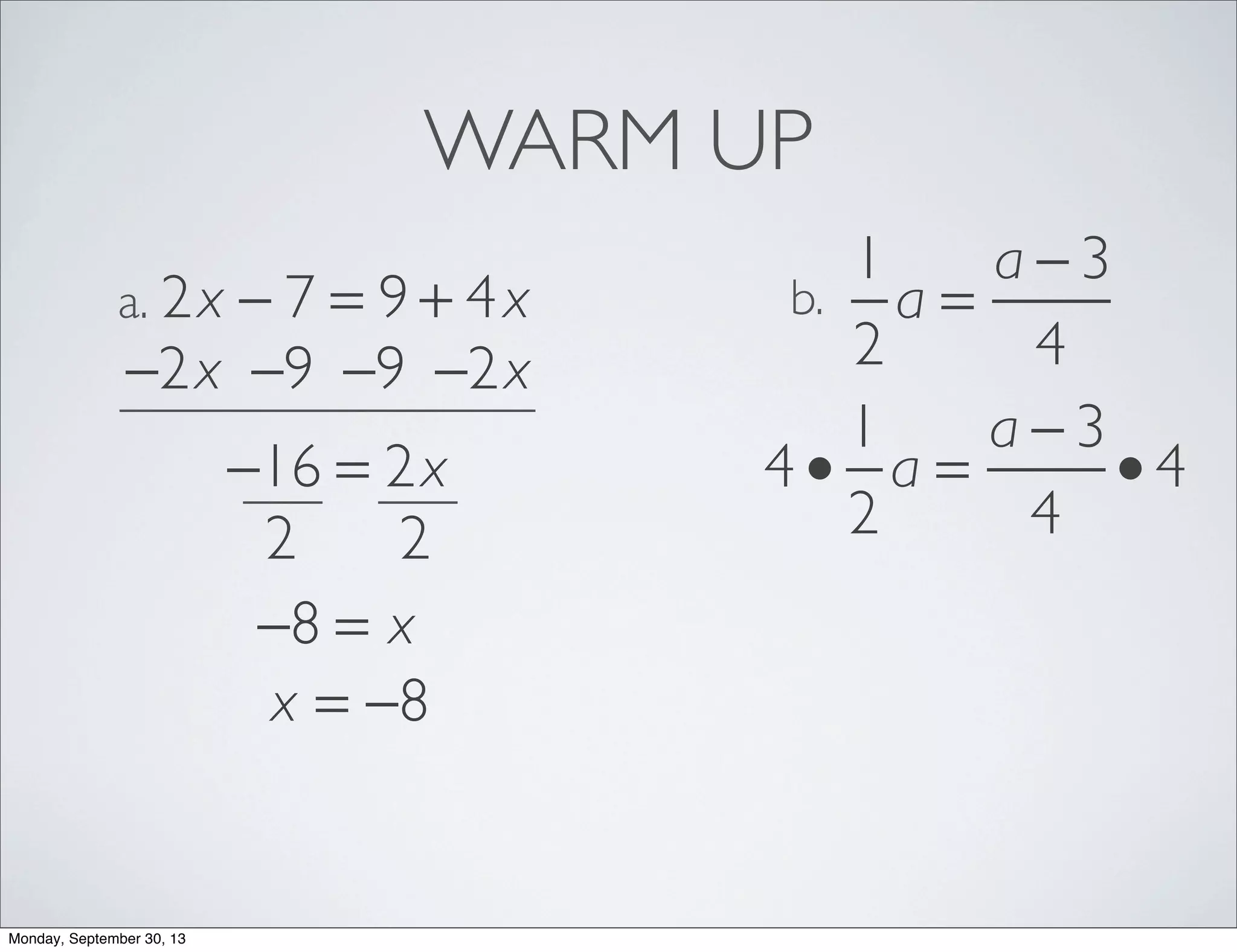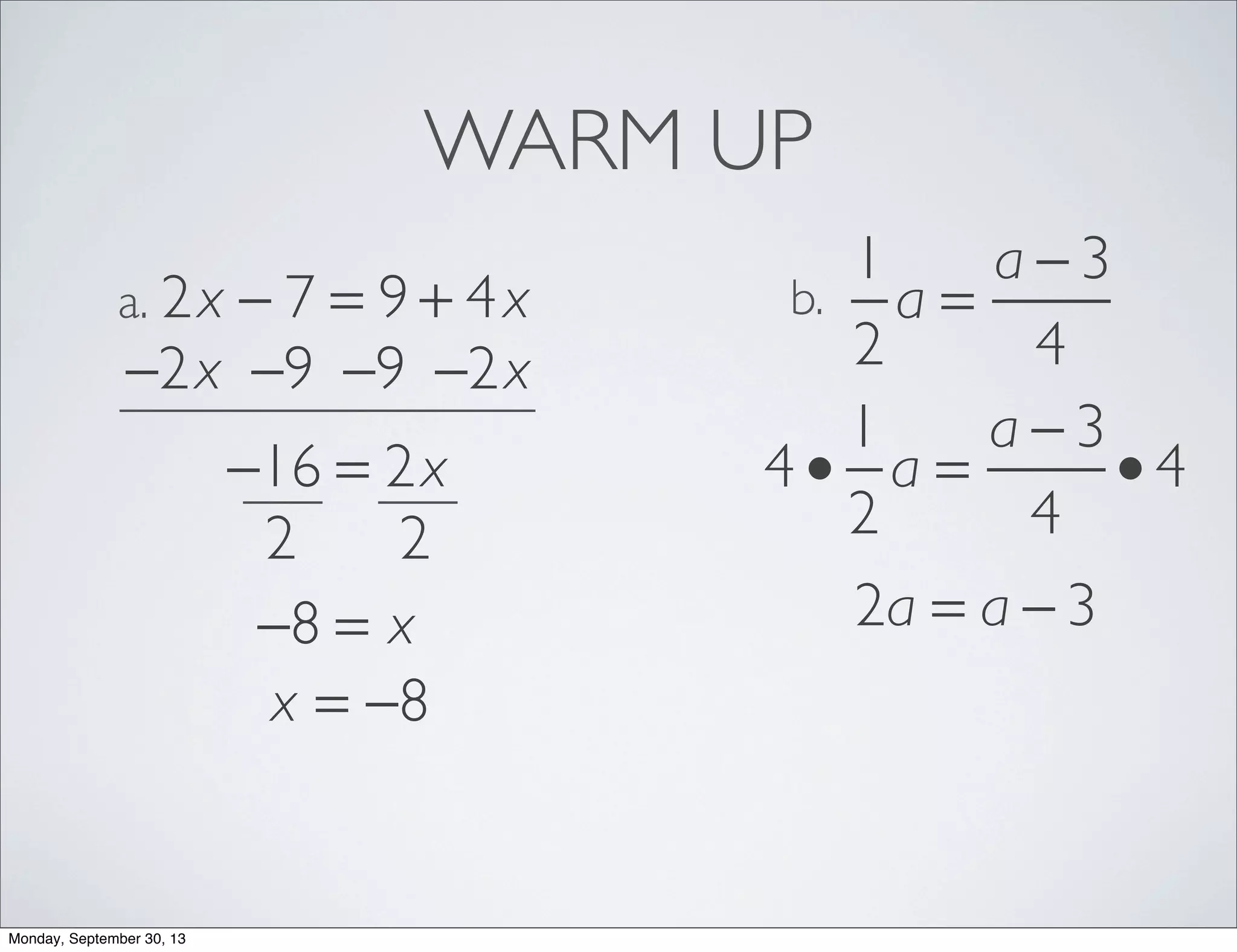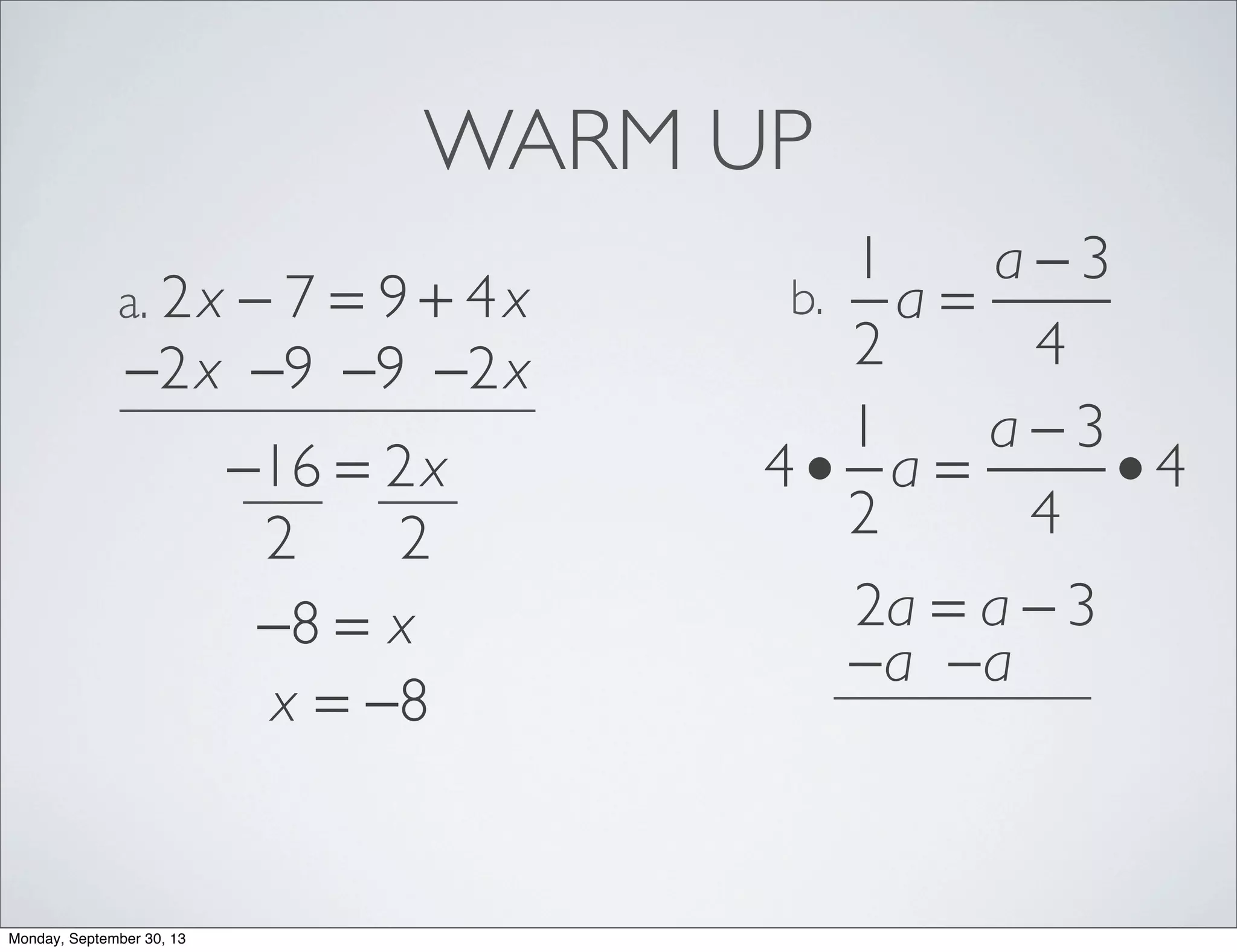The document provides examples for solving multi-step inequalities. It begins with a warm up problem solving a multi-step equation. It then provides 4 examples of setting up and solving multi-step inequalities, identifying a variable, writing an inequality, solving for the variable and interpreting the solution. The examples involve word problems relating to budgets, numbers and variables in algebraic expressions.

1. SECTION 5-3
Solving Multi-Step Inequalities
Monday, September 30, 13

2. ESSENTIAL QUESTION
• How do we solve multi-step inequalities?
Monday, September 30, 13

3. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
Monday, September 30, 13

4. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x
Monday, September 30, 13

5. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x
Monday, September 30, 13

6. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9
Monday, September 30, 13

7. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
Monday, September 30, 13

8. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
Monday, September 30, 13

9. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
Monday, September 30, 13

10. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
Monday, September 30, 13

11. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
Monday, September 30, 13

12. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
x = −8
Monday, September 30, 13

13. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
x = −8
4 •
1
2
a =
a − 3
4
• 4
Monday, September 30, 13

14. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
x = −8
4 •
1
2
a =
a − 3
4
• 4
2a = a − 3
Monday, September 30, 13

15. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
x = −8
4 •
1
2
a =
a − 3
4
• 4
2a = a − 3
−a−a
Monday, September 30, 13

16. WARM UP
2x − 7 = 9 + 4xa.
1
2
a =
a − 3
4
b.
−2x −2x−9−9
−16 = 2x
22
−8 = x
x = −8
4 •
1
2
a =
a − 3
4
• 4
2a = a − 3
−a−a
a = −3
Monday, September 30, 13

17. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
Monday, September 30, 13

18. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
Monday, September 30, 13

19. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
Monday, September 30, 13

20. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
Monday, September 30, 13

21. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
.08p ≤ 90
Monday, September 30, 13

22. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
.08p ≤ 90
.08 .08
Monday, September 30, 13

23. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
.08p ≤ 90
.08 .08
p ≤1125
Monday, September 30, 13

24. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
.08p ≤ 90
.08 .08
p ≤1125
p | p ≤1125{ }
Monday, September 30, 13

25. EXAMPLE 1
Maggie Brann has a budget of $115 for faxes.The fax
service she uses charges $25 to activate an account and
$0.08 per page to send faxes. How many pages can she
fax and stay within her budget? Identify a variable, then set
up and solve an inequality. Interpret your solution.
p = pages she can fax
25+ .08p ≤115
−25 −25
.08p ≤ 90
.08 .08
p ≤1125
p | p ≤1125{ }
Maggie can send up to
1125 faxes.
Monday, September 30, 13

26. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
Monday, September 30, 13

27. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
−13 −13
Monday, September 30, 13

28. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
−13 −13
−11d ≥ 66
Monday, September 30, 13

29. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
−13 −13
−11d ≥ 66
−11 −11
Monday, September 30, 13

30. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
−13 −13
−11d ≥ 66
−11 −11
d ≤ −6
Monday, September 30, 13

31. EXAMPLE 2
Solve the inequality.
13−11d ≥ 79
−13 −13
−11d ≥ 66
−11 −11
d ≤ −6
d | d ≤ −6{ }
Monday, September 30, 13

32. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
Monday, September 30, 13

33. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
Monday, September 30, 13

34. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
Monday, September 30, 13

35. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
Monday, September 30, 13

36. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
Monday, September 30, 13

37. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
Monday, September 30, 13

38. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
3n < −15
Monday, September 30, 13

39. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
3n < −15
3n < −15
Monday, September 30, 13

40. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
3n < −15
3n < −15
3 3
Monday, September 30, 13

41. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
3n < −15
3n < −15
3 3
n < −5
Monday, September 30, 13

42. EXAMPLE 3
Define a variable, write an inequality and solve the
problem.Then check your solution.
Four times a number increased by twelve is less than the
difference of that number and three.
n = the number
4n +12 < n − 3
−n −n
3n +12 < −3
−12 −12
3n < −15
3n < −15
3 3
n < −5
n | n < −5{ }
Monday, September 30, 13

43. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
Monday, September 30, 13

44. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
Monday, September 30, 13

45. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
Monday, September 30, 13

46. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
Monday, September 30, 13

47. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
Monday, September 30, 13

48. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
−6 −6
Monday, September 30, 13

49. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
−6 −6
5c > −5
Monday, September 30, 13

50. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
−6 −6
5c > −5
5 5
Monday, September 30, 13

51. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
−6 −6
5c > −5
5 5
c > −1
Monday, September 30, 13

52. EXAMPLE 4
6c + 3(2 − c) > −2c +1a.
6c + 6 − 3c > −2c +1
3c + 6 > −2c +1
+2c +2c
5c + 6 > +1
−6 −6
5c > −5
5 5
c > −1
c | c > −1{ }
Monday, September 30, 13

53. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
Monday, September 30, 13

54. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
Monday, September 30, 13

55. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
4k − 28 ≥ 4k −1
Monday, September 30, 13

56. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
4k − 28 ≥ 4k −1
−4k −4k
Monday, September 30, 13

57. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
4k − 28 ≥ 4k −1
−4k −4k
−28 ≥ −1
Monday, September 30, 13

58. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
4k − 28 ≥ 4k −1
−4k −4k
−28 ≥ −1
This is an untrue statement!
Monday, September 30, 13

59. EXAMPLE 4
−7(k + 4)+11k ≥ 8k − 2(2k +1)b.
−7k − 28 +11k ≥ 8k − 4k −1
4k − 28 ≥ 4k −1
−4k −4k
−28 ≥ −1
This is an untrue statement!
∅
Monday, September 30, 13

60. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
Monday, September 30, 13

61. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
Monday, September 30, 13

62. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
Monday, September 30, 13

63. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
Monday, September 30, 13

64. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
6 ≤ 6
Monday, September 30, 13

65. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
6 ≤ 6
This is a true statement!
Monday, September 30, 13

66. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
6 ≤ 6
This is a true statement!
r | r is any real number{ }
Monday, September 30, 13

67. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
6 ≤ 6
This is a true statement!
r | r is any real number{ }
or
Monday, September 30, 13

68. EXAMPLE 4
2(4r + 3) ≤ 22 + 8(r − 2)c.
8r + 6 ≤ 22 + 8r −16
8r + 6 ≤ 8r + 6
−8r −8r
6 ≤ 6
This is a true statement!
r | r is any real number{ }
r | r = { }
or
Monday, September 30, 13

69. SUMMARIZER
−3p + 7 > 2How could you solve without multiplying
or dividing each side by a negative number.
Monday, September 30, 13

70. PROBLEM SETS
Monday, September 30, 13

71. PROBLEM SETS
Problem Set 1: p. 298 #1-11
Problem Set 2: p. 298 #13-39 odd (skip #37),
"The secret of success in life is for a man to be ready for
his opportunity when it comes."
- Earl of Beaconsfield
Monday, September 30, 13