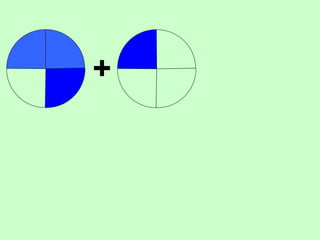
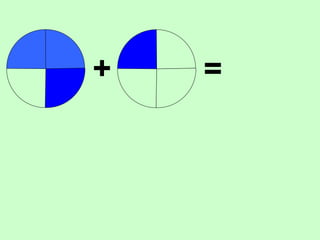
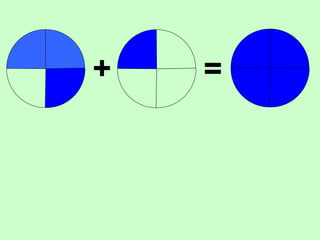
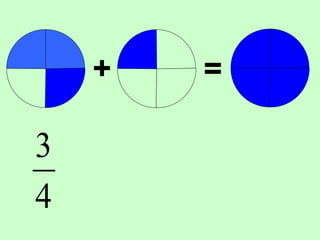
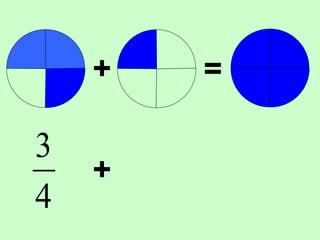
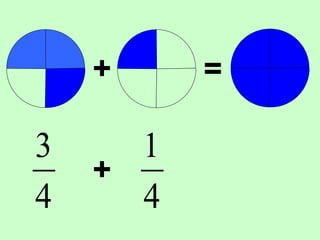
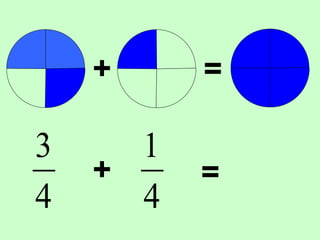
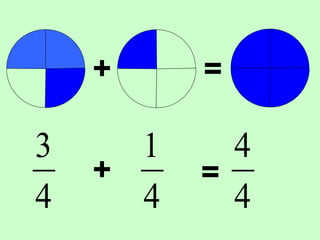
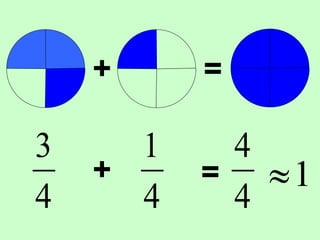
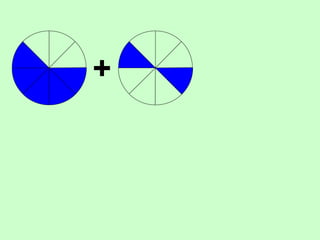
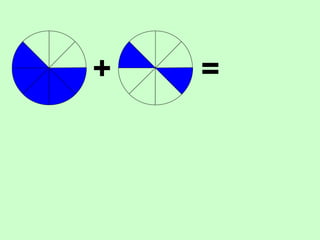
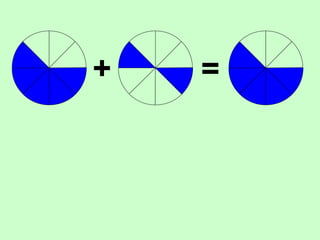
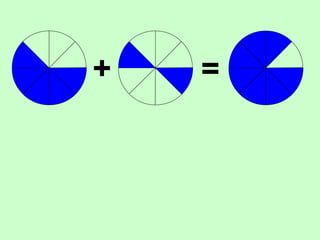
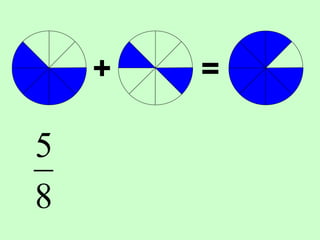
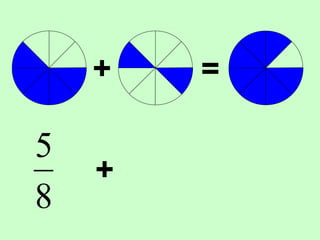
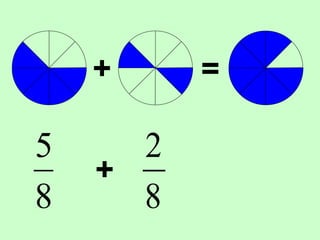
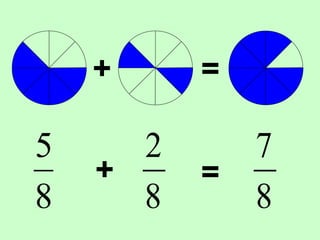
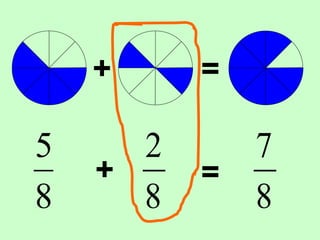
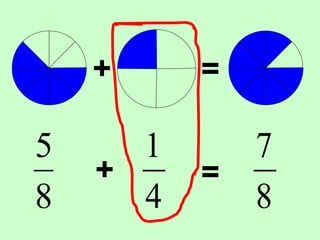
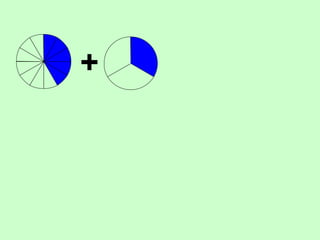
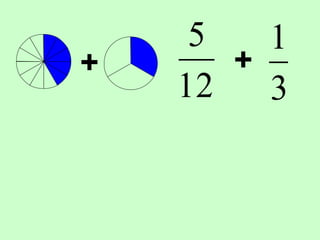
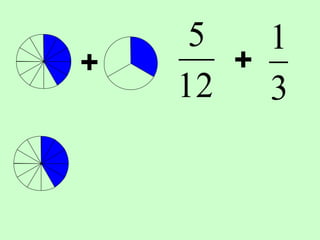
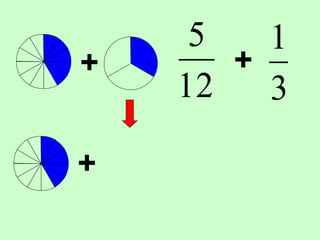
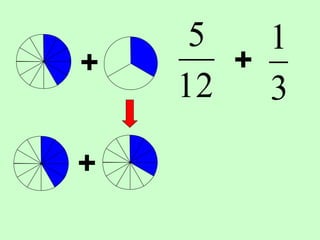
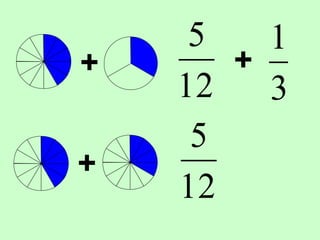
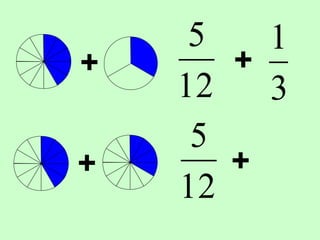
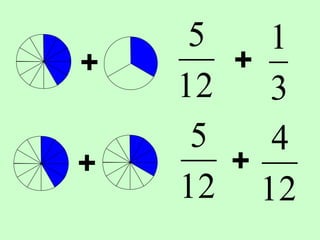
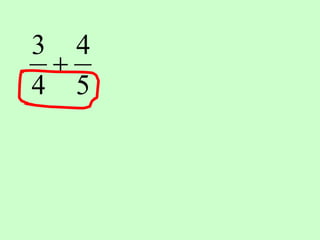
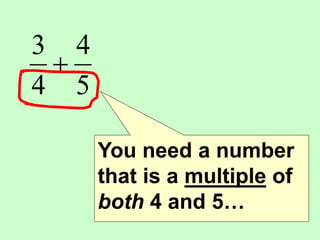
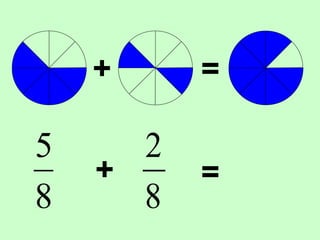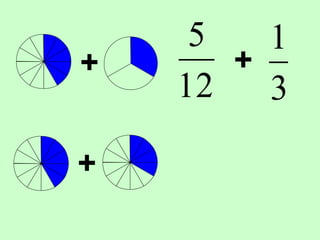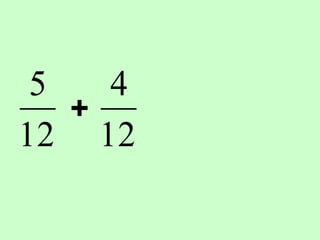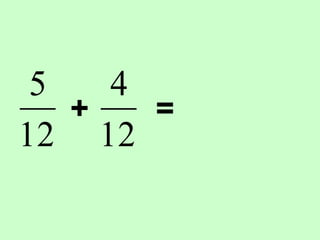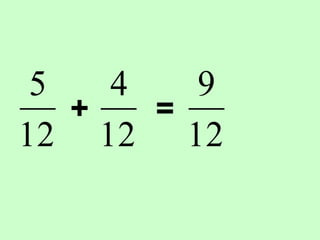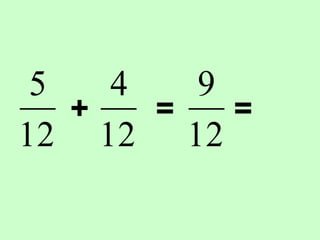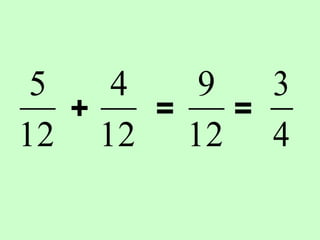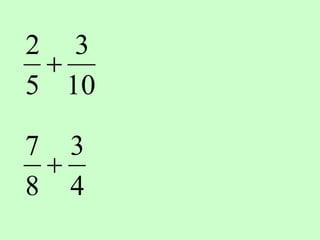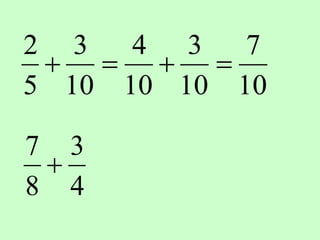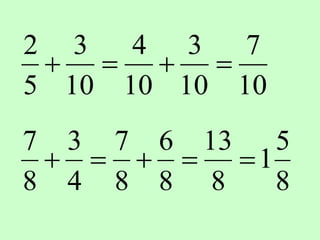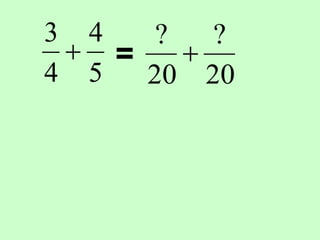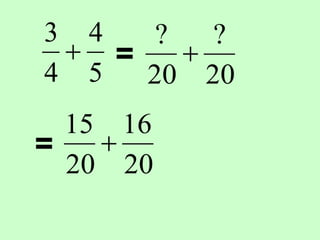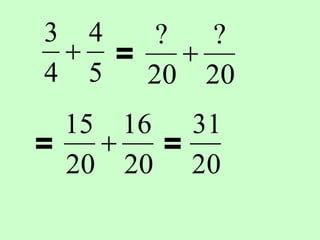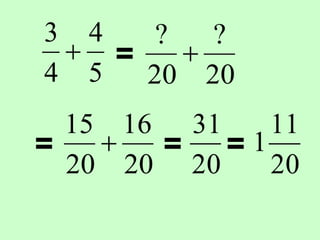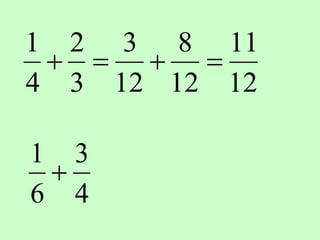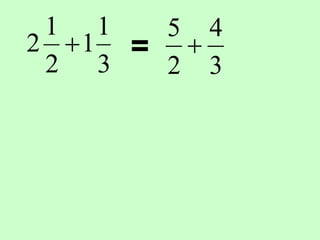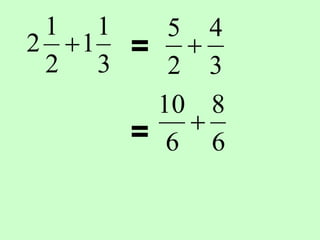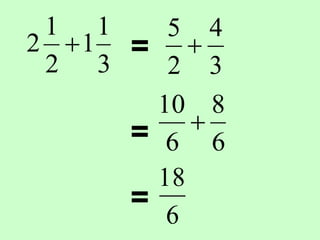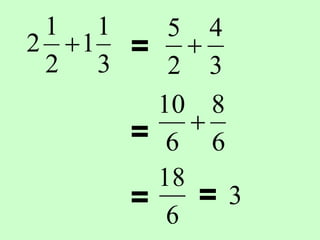The document covers the process of adding fractions, including how to handle fractions with the same and different denominators. It outlines steps such as checking denominators, finding equivalent fractions, and adding numerators. The document provides examples and encourages practice with exercises.

1. Adding Fractions

2. +

3. + =

4. + =

5. + =
4
3

6. + =
4
3
+

7. + =
4
3
4
1
+

8. + =
4
3
4
1
+ =

9. + =
4
3
4
1
+ =
4
4

10. + =
4
3
4
1
+ =
4
4
1

11. Same
denominators: add
the numerators!

12. +

13. + =

14. + =

15. + =

16. + =
8
5

17. + =
8
5
+

18. + =
8
5
8
2
+

19. + =
8
5
8
2
+ =

20. + =
8
5
8
2
+ =
8
7

21. + =
8
5
8
2
+ =
8
7

22. + =
8
5
4
1
+ =
8
7

23. If the denominators
are different, find
equivalent fractions,
then add numerators

24. +

25. +
12
5
+
3
1

26. +
12
5
+
3
1

27. +
+
12
5
+
3
1

28. +
+
12
5
+
3
1

29. +
+
12
5
+
3
1

30. +
+
12
5
+
3
1
12
5

31. +
+
12
5
+
3
1
12
5
+

32. +
+
12
5
+
3
1
12
5
+
12
4

33. 12
5
+
12
4

34. 12
5
+
12
4
=

35. 12
5
+
12
4
12
9
=

36. 12
5
+
12
4
12
9
= =

37. 12
5
+
12
4
12
9
= =
4
3

38. 1. Check denominators

39. 1. Check denominators
2. Find equivalent fractions so
denominators same

40. 1. Check denominators
2. Find equivalent fractions so
denominators same
3. Add numerators

41. 1. Check denominators
2. Find equivalent fractions so
denominators same
3. Add numerators
4. Cancel down if needed

42. 1. Check denominators
2. Find equivalent fractions so
denominators same
3. Add numerators
4. Cancel down if needed
5. Pull out the whole numbers
if needed

43. Your turn…

44. 10
3
5
2

4
3
8
7


45. 10
7
10
3
10
4
10
3
5
2

4
3
8
7


46. 10
7
10
3
10
4
10
3
5
2

8
5
1
8
13
8
6
8
7
4
3
8
7


47. Sometimes, you
have to change both
denominators…

48. 5
4
4
3


49. 5
4
4
3


50. 5
4
4
3

You need a number
that is a multiple of
both 4 and 5…

51. 5
4
4
3
 =
20
?
20
?


52. 5
4
4
3
 =
20
?
20
?

=
20
16
20
15


53. 5
4
4
3
 =
20
?
20
?

=
20
16
20
15
 =
20
31

54. 5
4
4
3
 =
20
?
20
?

=
20
16
20
15
 =
20
31
=
20
11
1

55. 1. Check denominators

56. 1. Check denominators
2. Find ‘common
denominator’ (LCM)

57. 1. Check denominators
2. Find ‘common
denominator’ (LCM)
3. Add numerators

58. 1. Check denominators
2. Find ‘common
denominator’ (LCM)
3. Add numerators
4. Cancel down if needed

59. 1. Check denominators
2. Find ‘common
denominator’ (LCM)
3. Add numerators
4. Cancel down if needed
5. Pull out the whole numbers
if needed

60. Your turn…

61. 4
3
6
1

3
2
4
1


62. 12
11
12
8
12
3
3
2
4
1

4
3
6
1


63. 12
11
12
9
12
2
4
3
6
1

12
11
12
8
12
3
3
2
4
1


64. Sometimes, you
have to add fractions
larger than one…

65. 3
2
1
2
1
2 
I suggest making
these fractions
‘top heavy’.

66. 3
1
1
2
1
2 

67. 3
1
1
2
1
2  =
3
4
2
5


68. 3
1
1
2
1
2  =
3
4
2
5

6
8
6
10
=

69. 3
1
1
2
1
2  =
3
4
2
5

6
8
6
10
=
= 6
18

70. 3
1
1
2
1
2  =
3
4
2
5

6
8
6
10
=
= 6
18
= 3

71. Now find an exercise in
the book or a work-
sheet and practice!