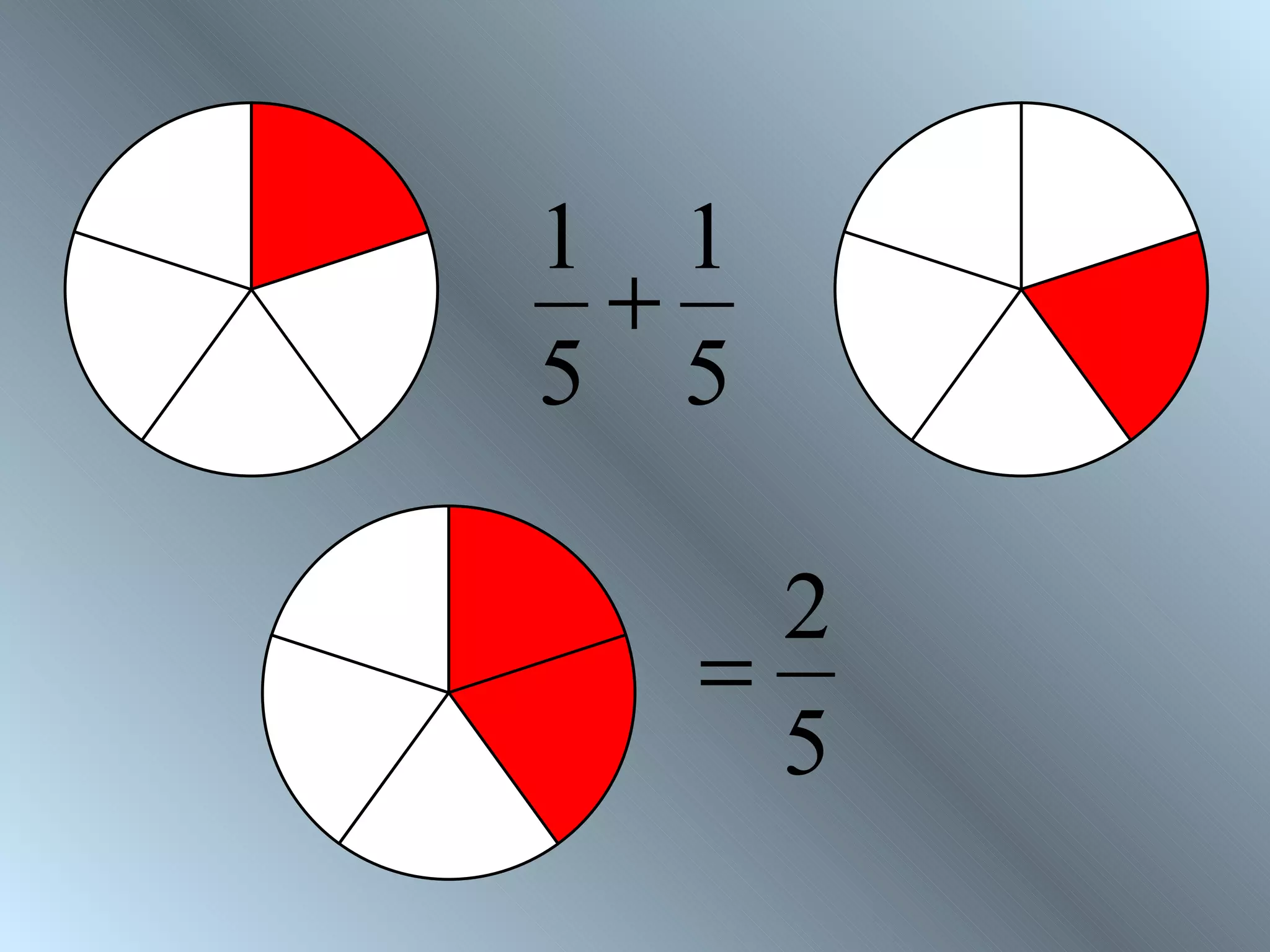
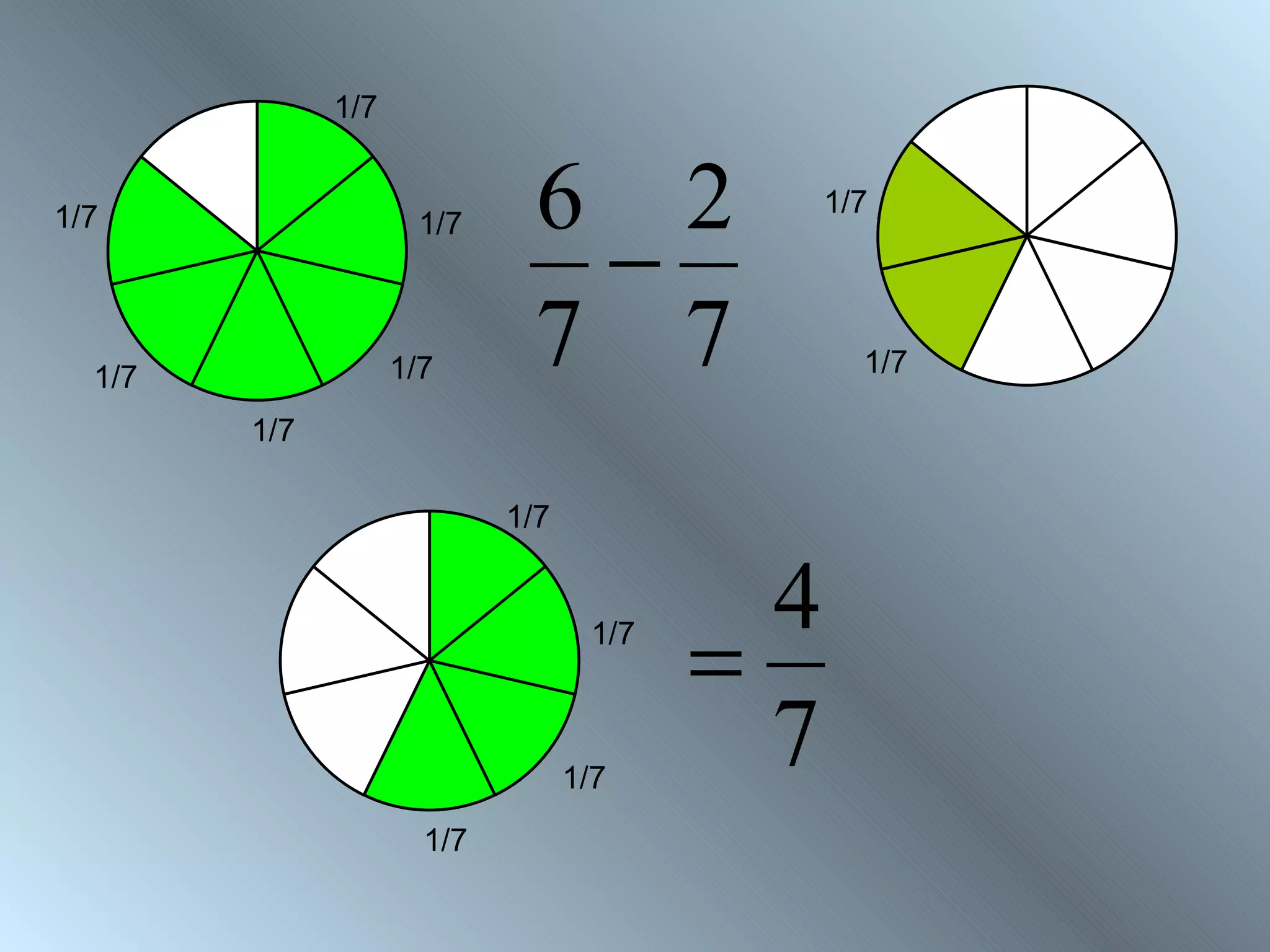
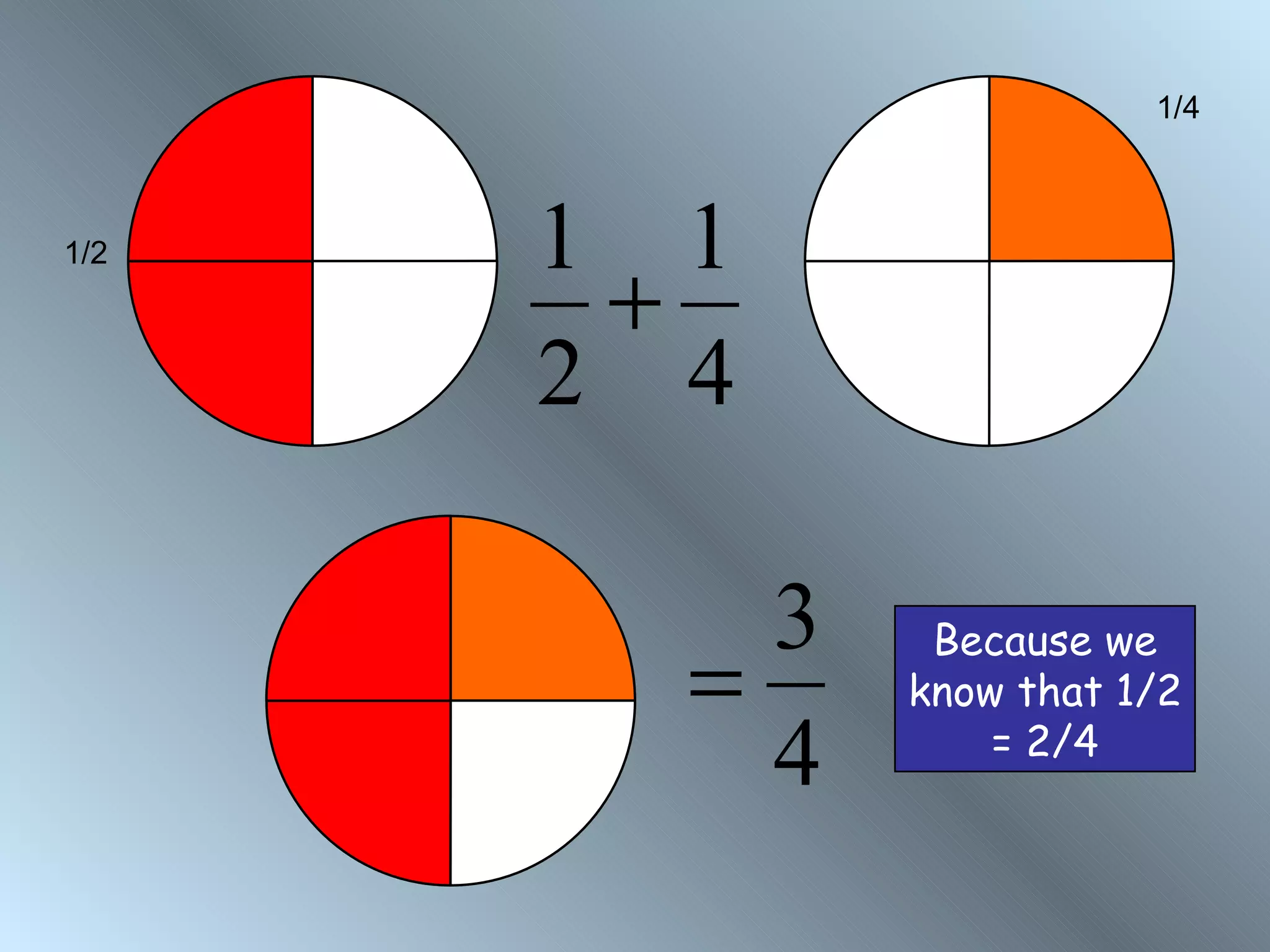
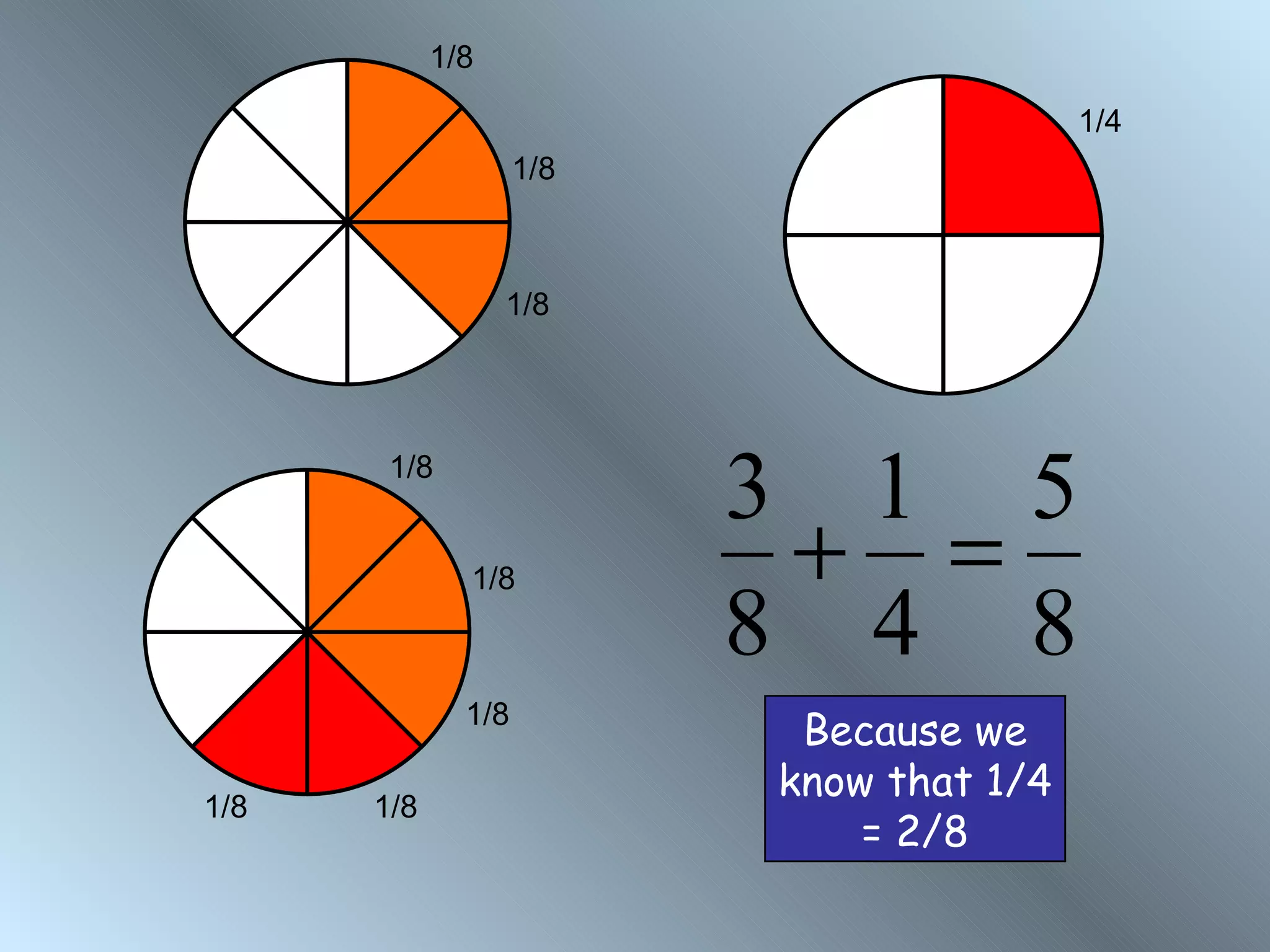
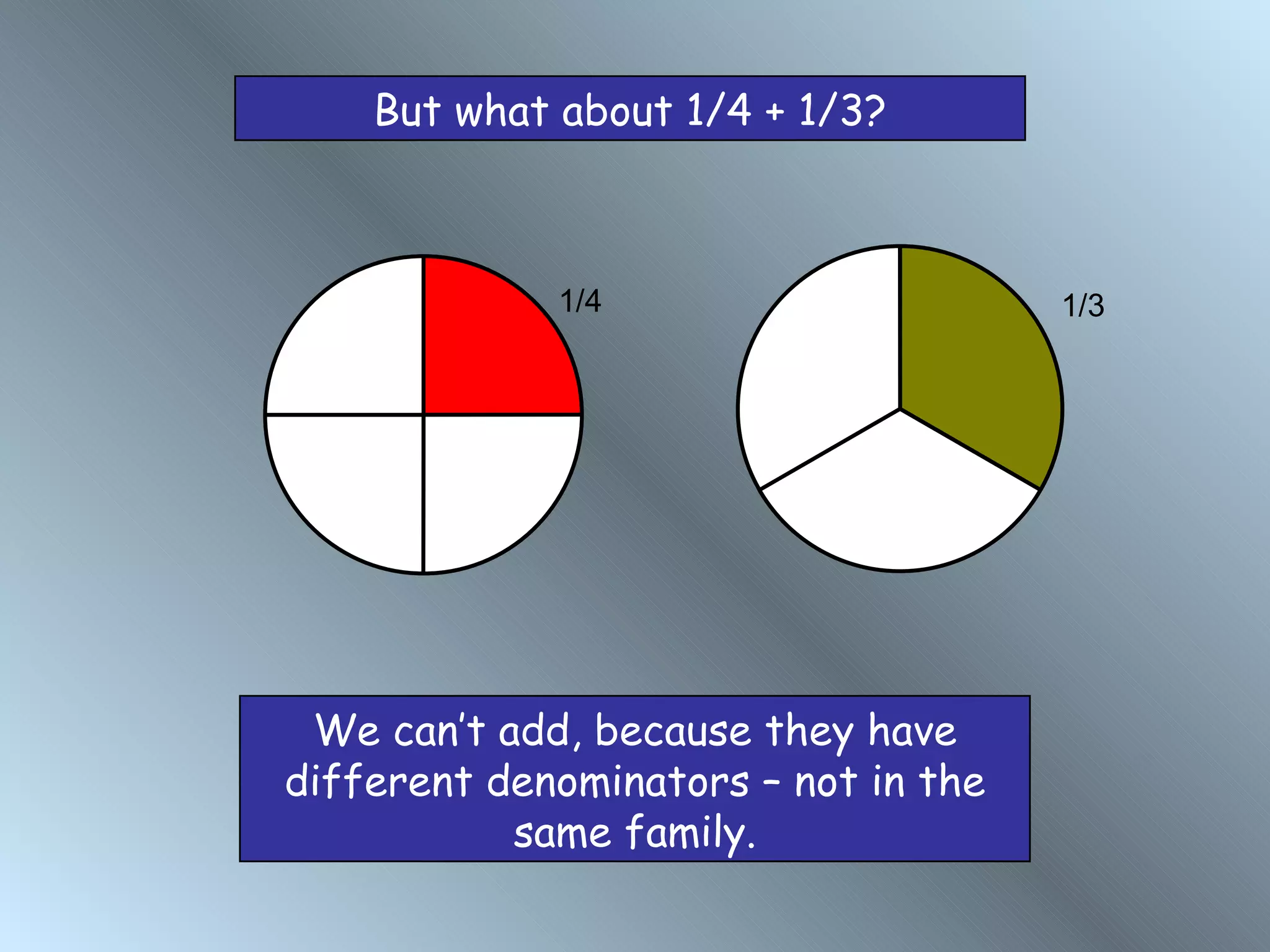
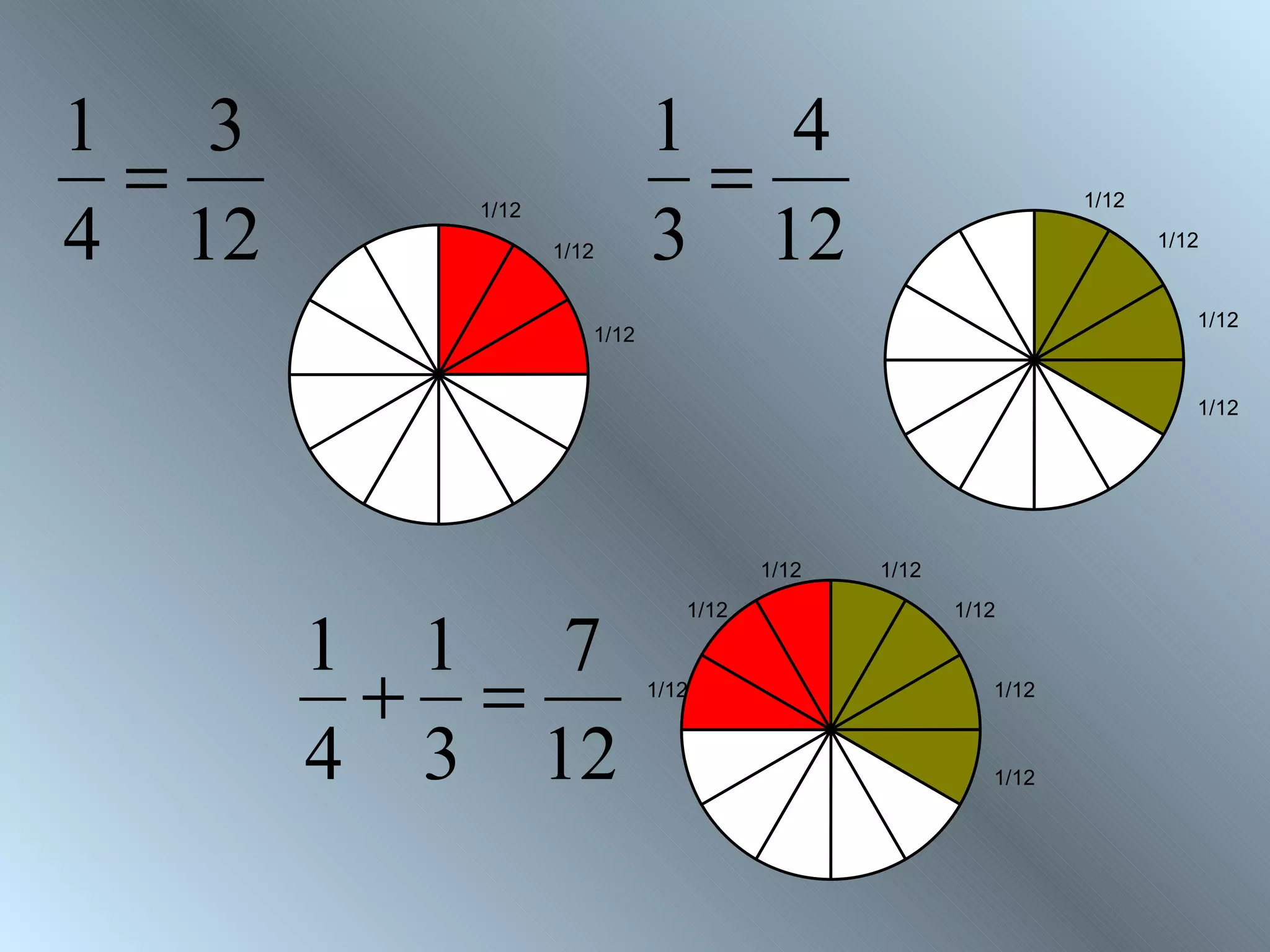
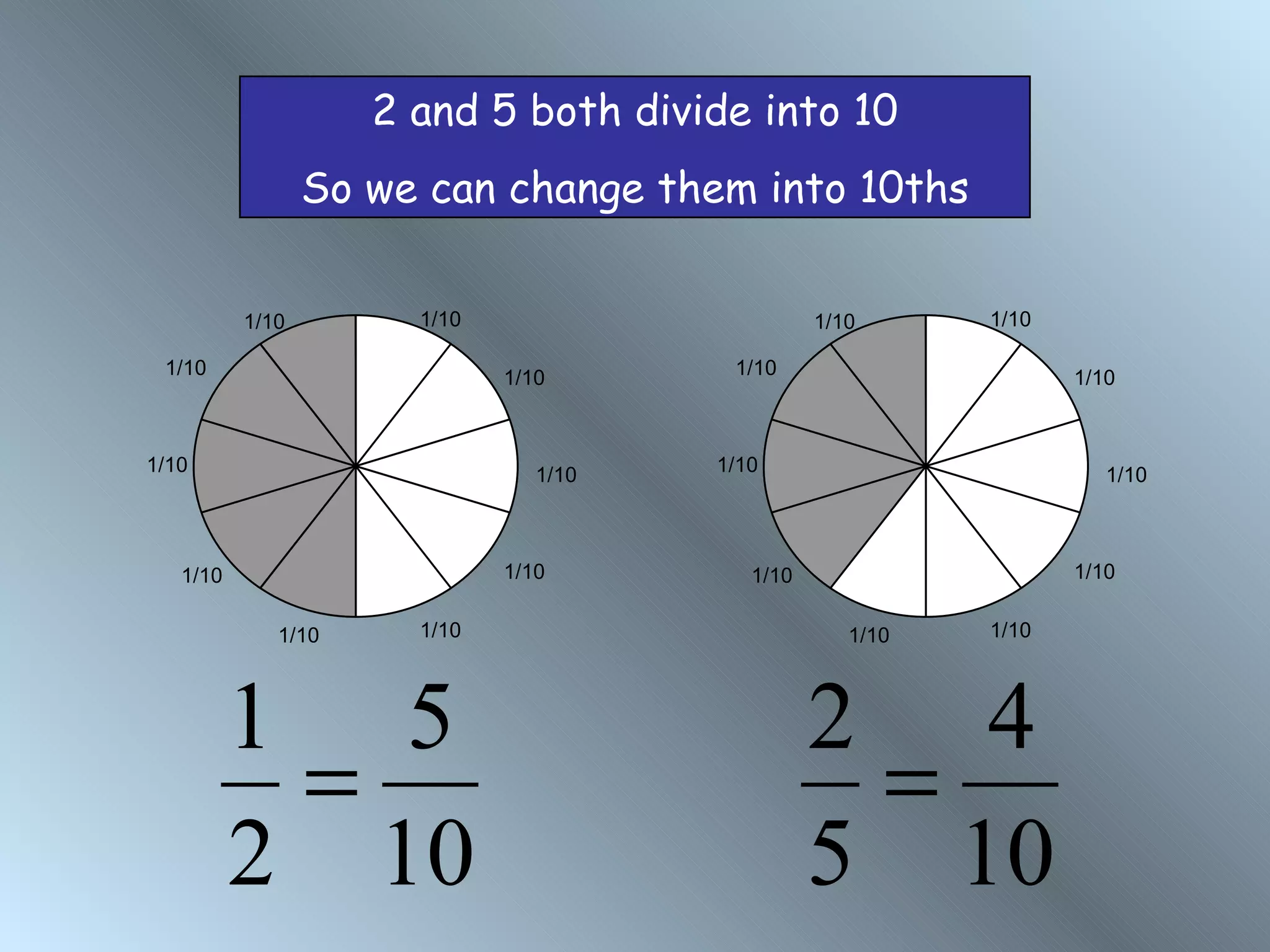
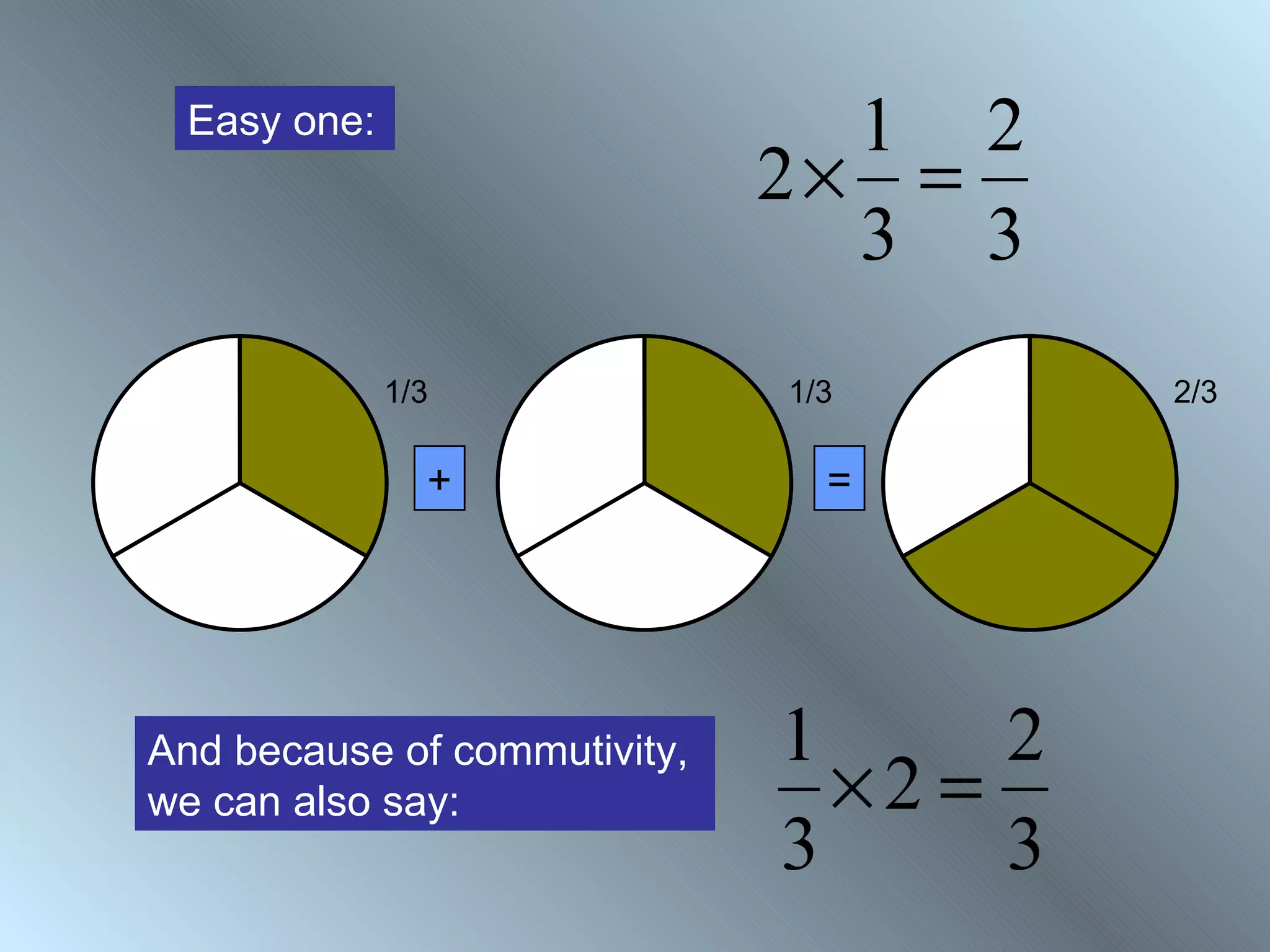
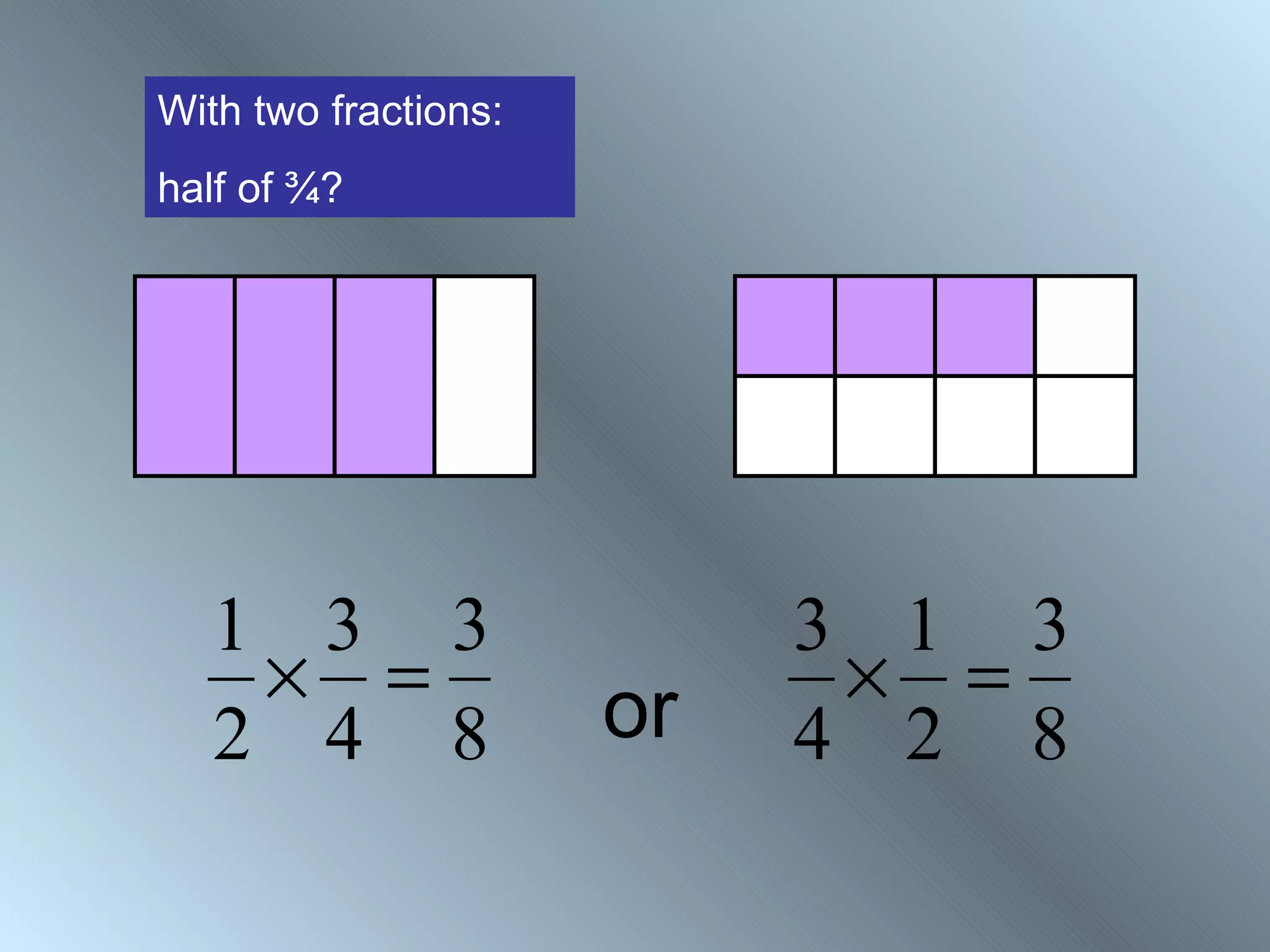
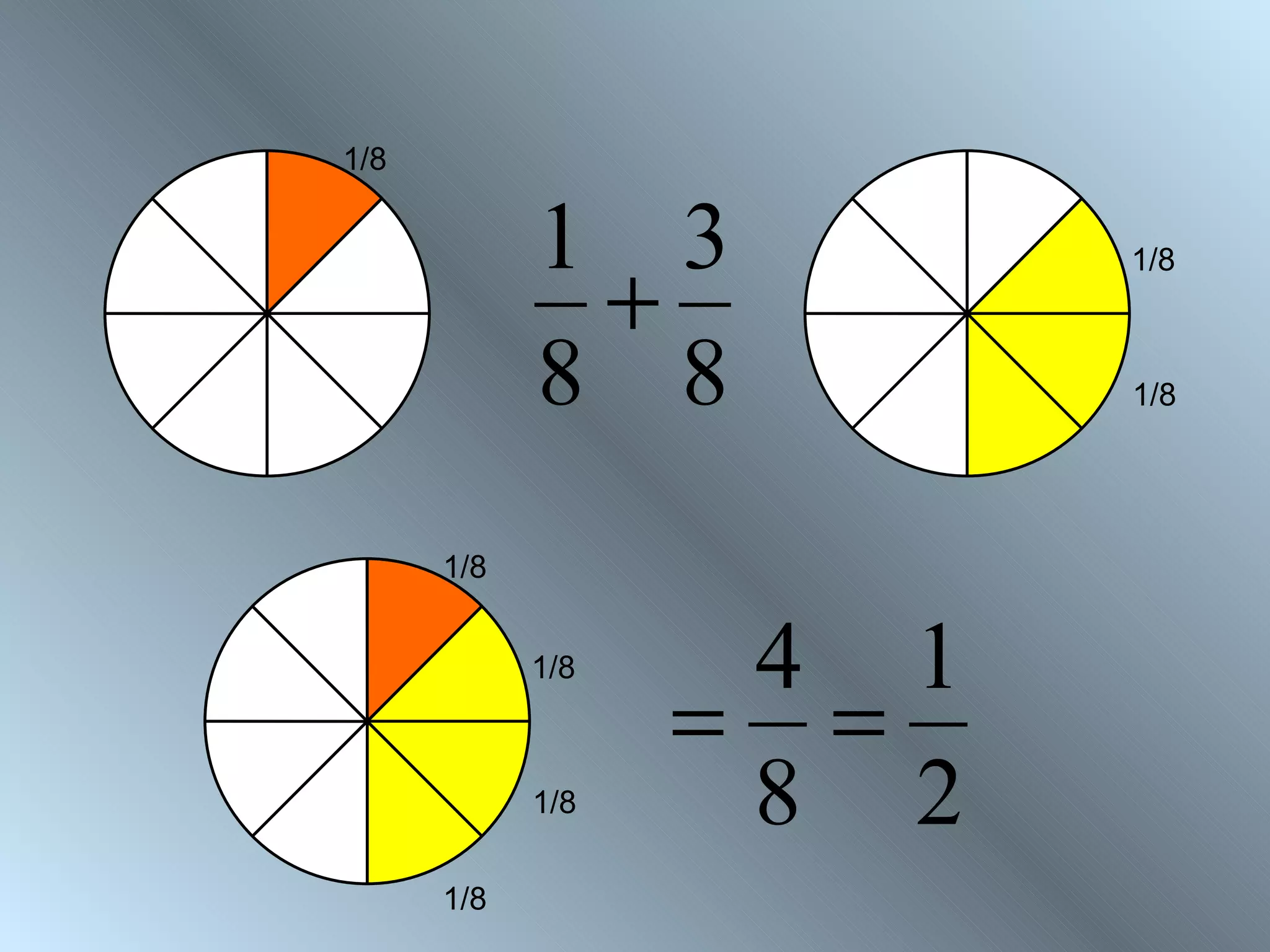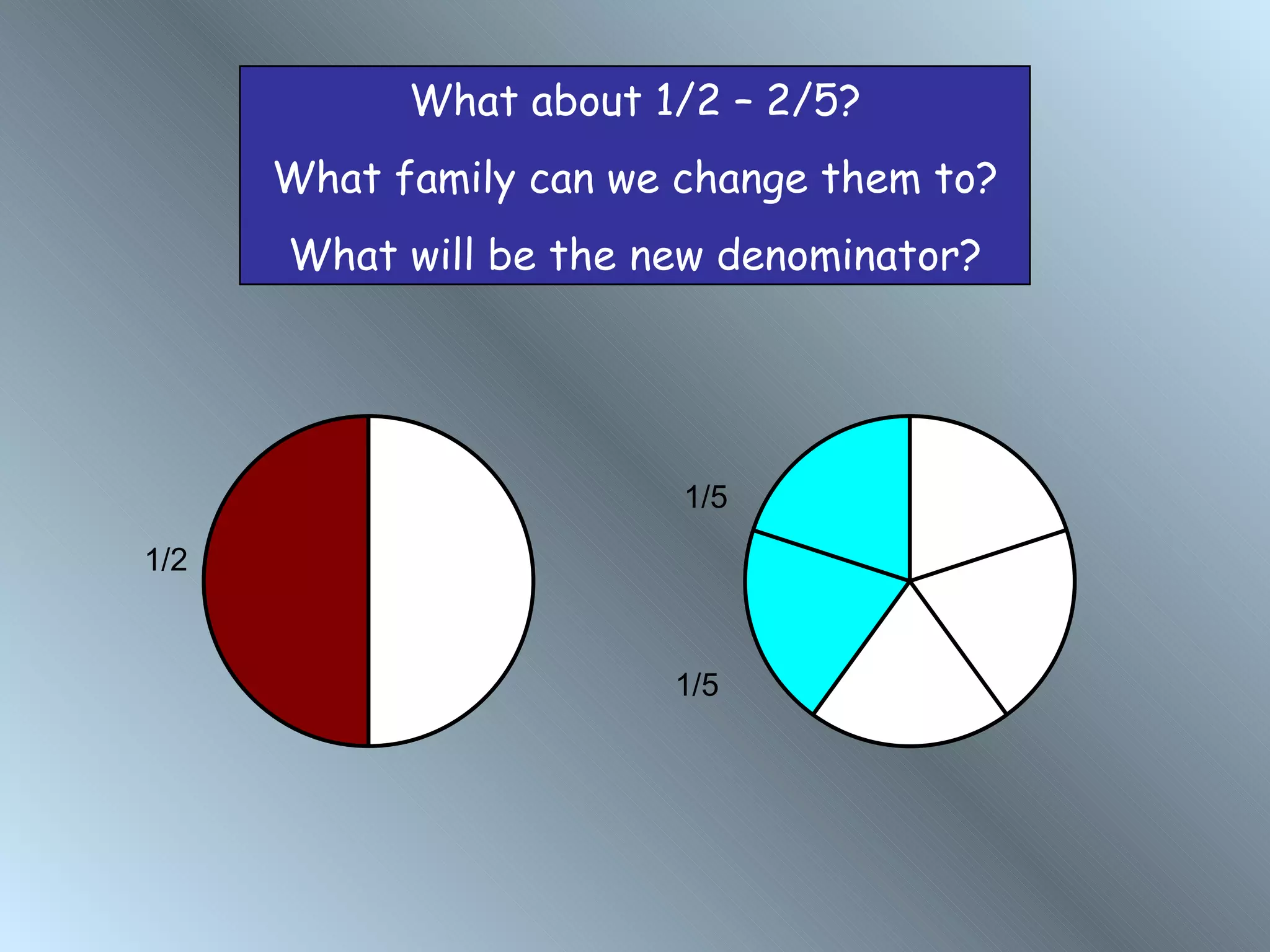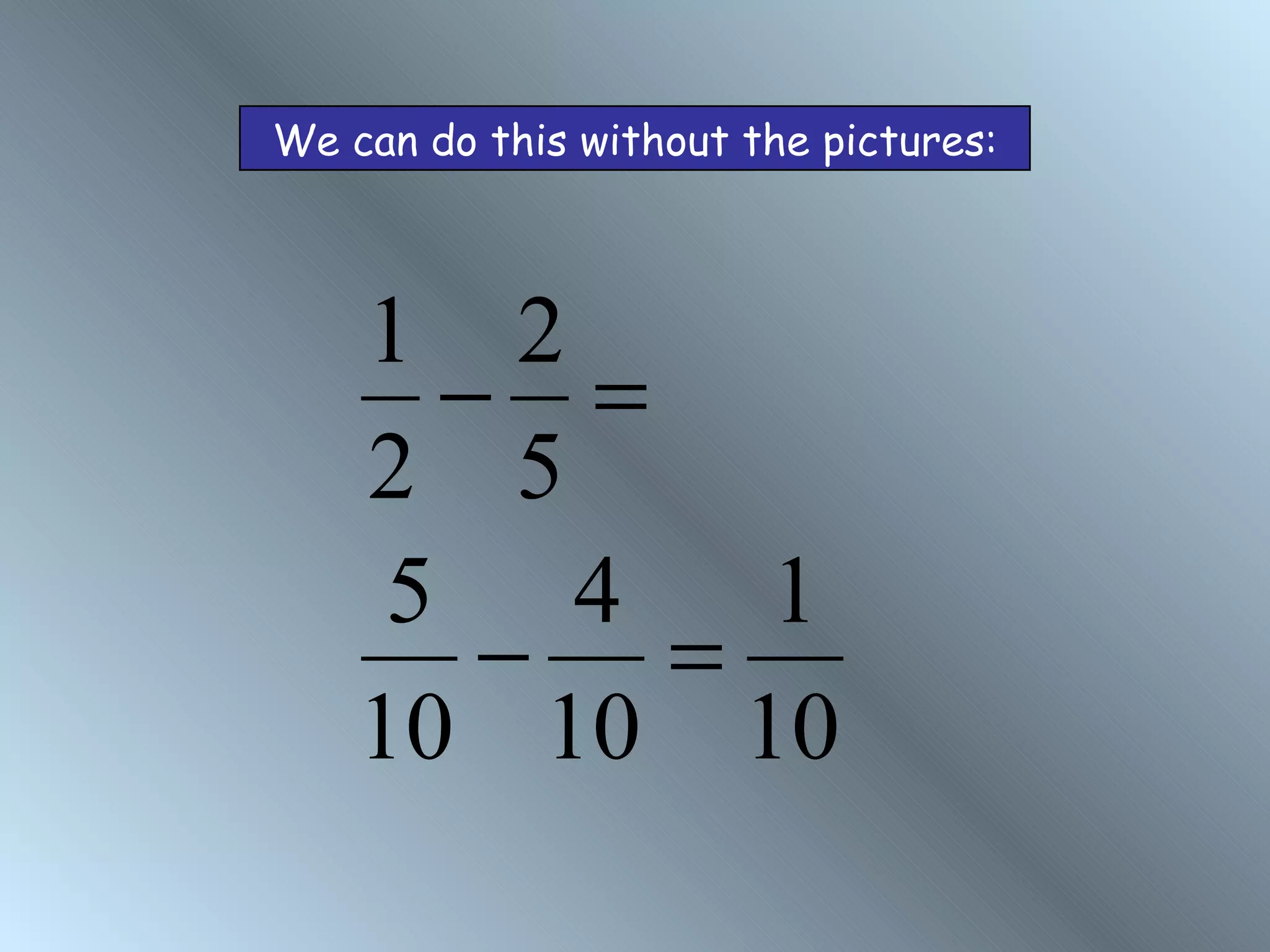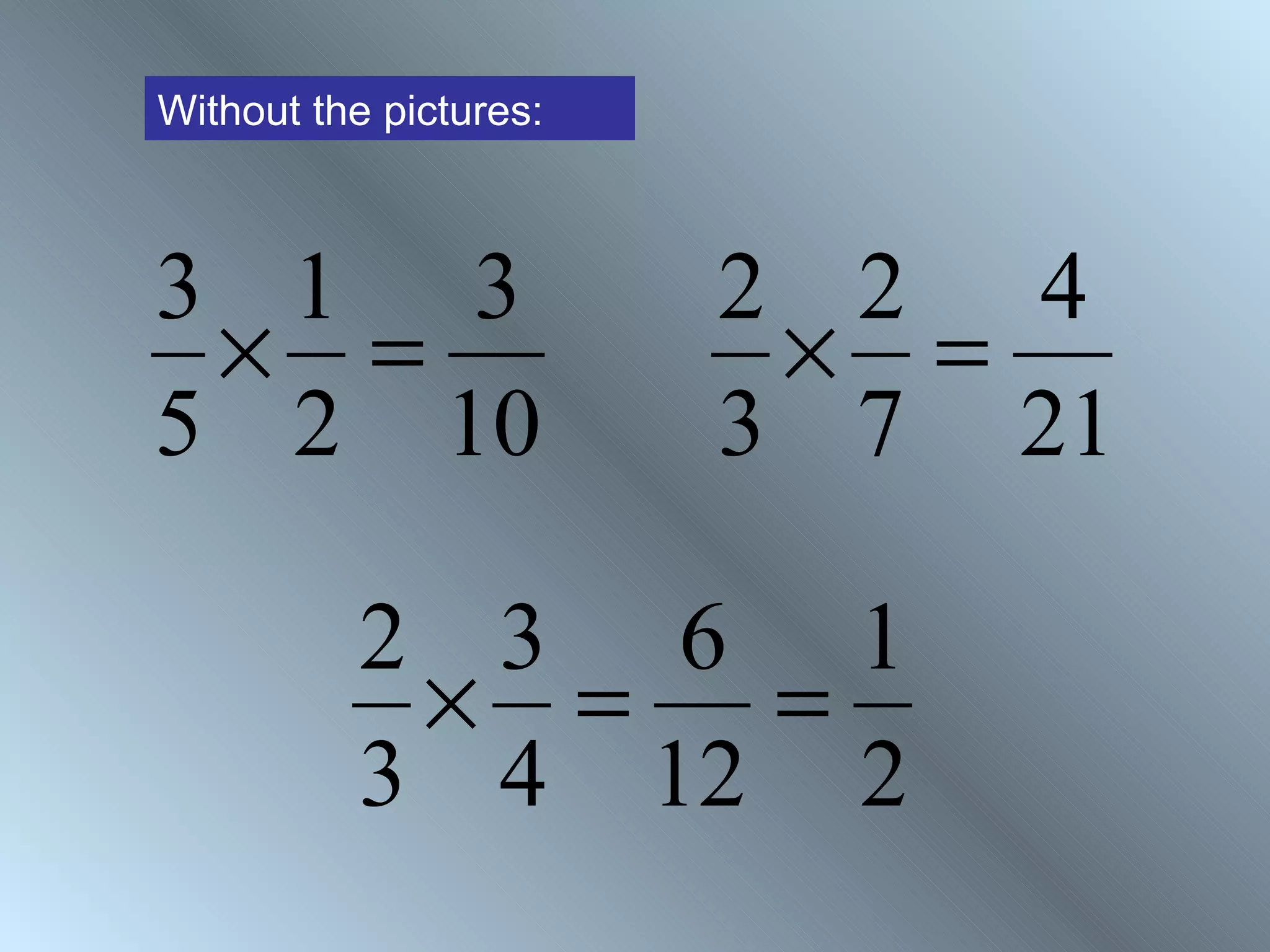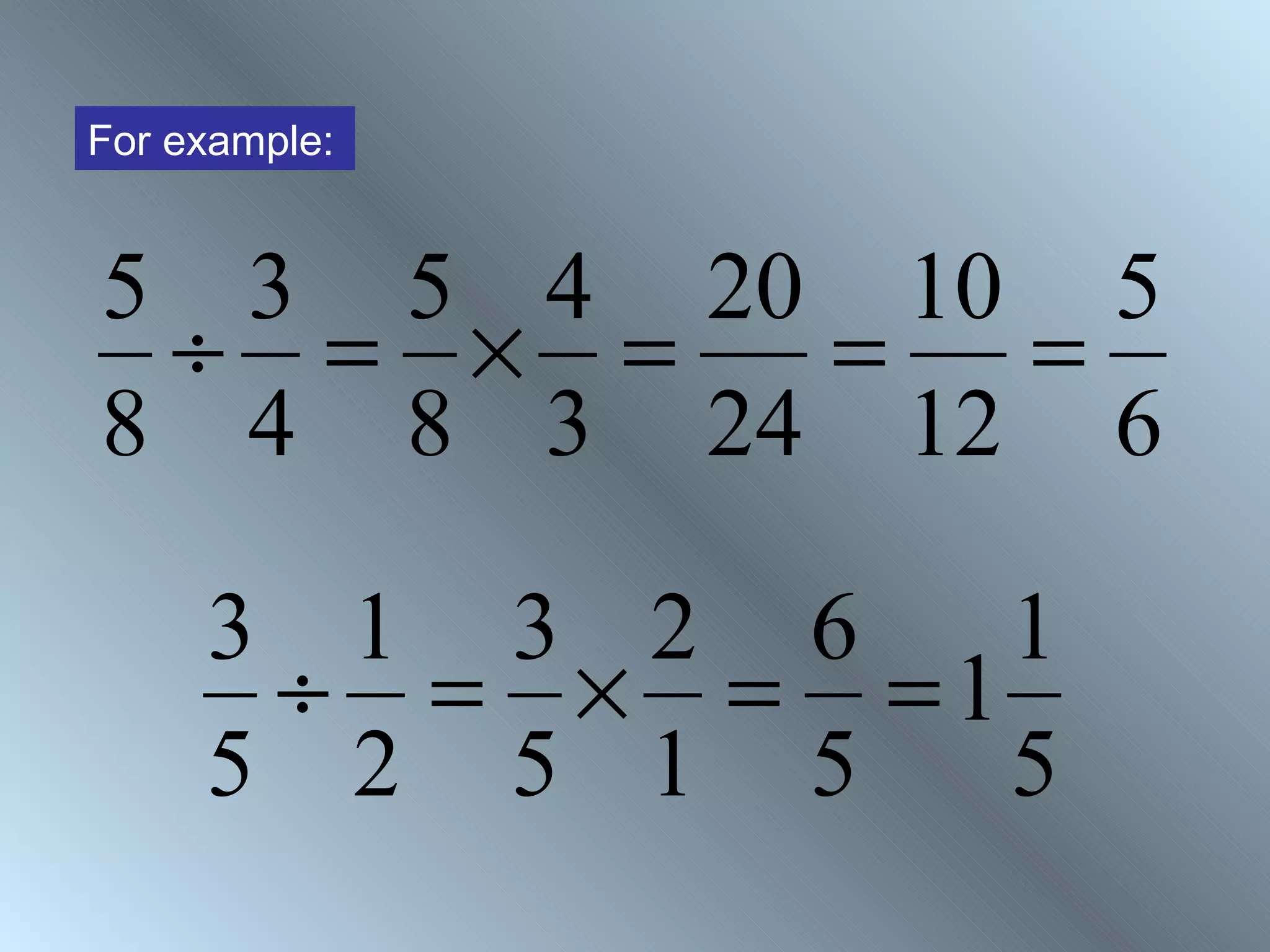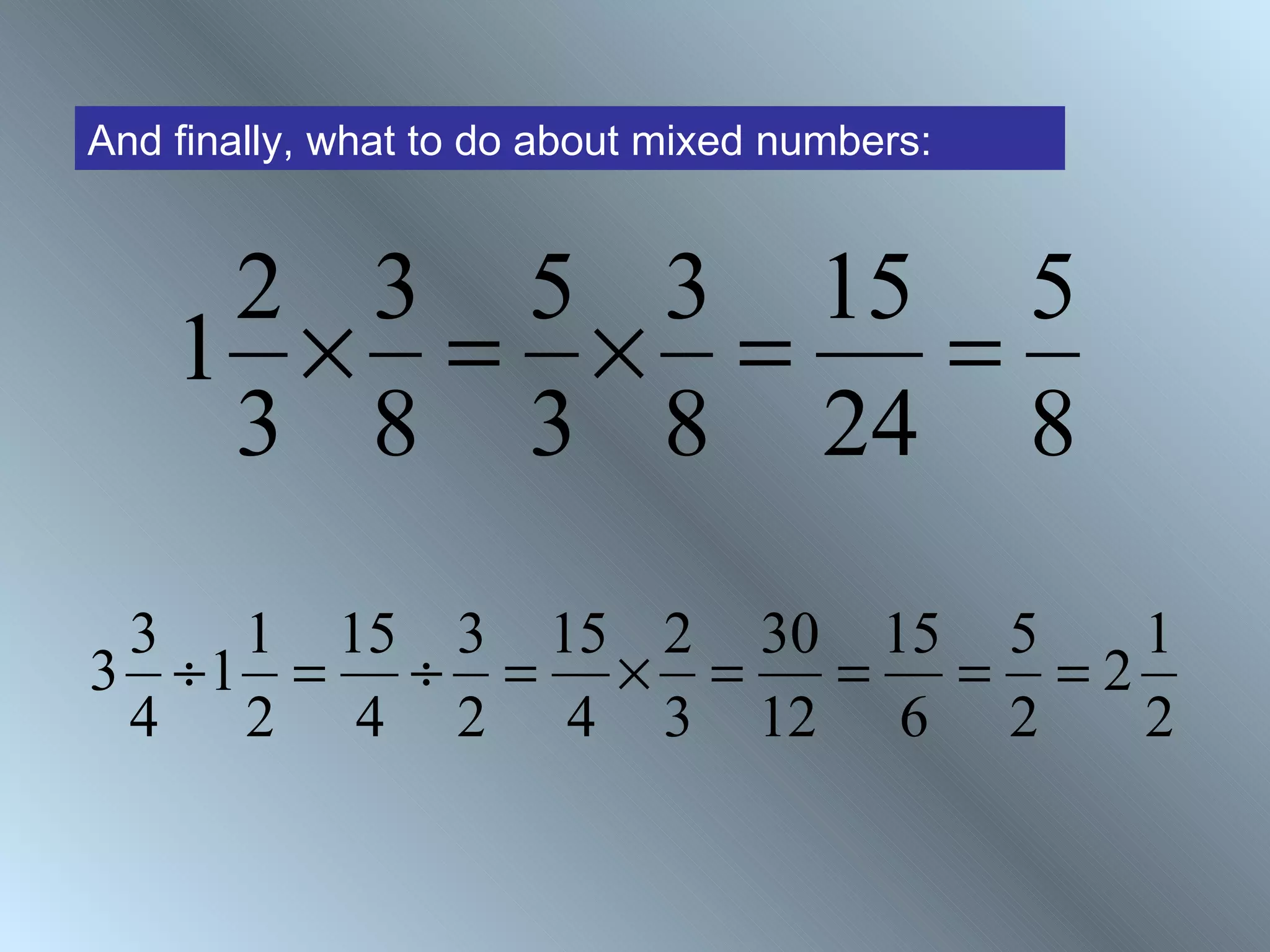The document discusses rules for adding, subtracting, multiplying, and dividing fractions. It explains that when adding or subtracting fractions, they must have a common denominator. It demonstrates converting fractions to equivalent fractions with a common denominator to allow for addition or subtraction. The document also covers multiplying and dividing fractions, showing examples like half of 3/4 and 3 1/3 divided by 4 2/3. It encourages practicing fraction operations with number cards and checking the work with a calculator.

1. Four rules of fractions
How to do

2. Addition and Subtraction
The simple bits

3. 1 1
+
5 5
2
=
5

4. 1/7
6 2 1/7
−
1/7 1/7
1/7 1/7 7 7 1/7
1/7
1/7
4
1/7
=
1/7
7
1/7

5. 1/8
1 3
+
1/8
8 8 1/8
1/8
1/8 4 1
= =
1/8 8 2
1/8

6. Why were they so simple?
• Because they all had the same
denominator
• They were all from the same families
What if they are of different
families?

7. 1/4
1 1
+
1/2
2 4
3 Because we
= know that 1/2
4 = 2/4

8. 1/8
1/4
1/8
1/8
1/8
3 1 5
1/8 + =
8 4 8
1/8
Because we
know that 1/4
1/8 1/8
= 2/8

9. But what about 1/4 + 1/3?
1/4 1/3
We can’t add, because they have
different denominators – not in the
same family.

10. What family can we change them to?
What will be the new denominator?
1/4 1/3
4 and 3 both divide into 12
So we can change them into 12ths

11. 1 3 1 4
= = 1/12
4 12 3 12
1/12
1/12
1/12
1/12
1/12
1/12
1/12 1/12
1/12 1/12
1 1 7
+ = 1/12 1/12
4 3 12 1/12

12. What about 1/2 – 2/5?
What family can we change them to?
What will be the new denominator?
1/5
1/2
1/5

13. 2 and 5 both divide into 10
So we can change them into 10ths
1/10 1/10 1/10 1/10
1/10 1/10 1/10 1/10
1/10 1/10 1/10 1/10
1/10 1/10 1/10 1/10
1/10 1/10 1/10 1/10
1 5 2 4
= =
2 10 5 10

14. We can do this without the pictures:
1 2
− =
2 5
5 4 1
− =
10 10 10

15. Make fractions using a
set of numbered cards,
and try some addition and
subtraction yourself.
Check them with a
calculator

16. Share one example from
your group with the rest
of the class.

17. Multiplication and Division

18. Easy one: 1 2
2× =
3 3
1/3 1/3 2/3
+ =
And because of commutivity, 1 2
we can also say: ×2 =
3 3

19. With two fractions:
half of ¾?
1 3 3 3 1 3
× = or × =
2 4 8 4 2 8

20. Without the pictures:
3 1 3 2 2 4
× = × =
5 2 10 3 7 21
2 3 6 1
× = =
3 4 12 2

21. And division?
Unfortunately, there is no easy way to
show diagrams for division of fractions.
Nor is there any obvious way of trying to make
sense of it.
The best thing is probably just to learn the
rule!

22. To divide by a fraction
• Do not change the first fraction
• Change the division sign into a
multiplication sign
• Turn the second fraction upside down
• Multiply the fractions

23. For example:
5 3 5 4 20 10 5
÷ = × = = =
8 4 8 3 24 12 6
3 1 3 2 6 1
÷ = × = =1
5 2 5 1 5 5

24. And finally, what to do about mixed numbers:
2 3 5 3 15 5
1 × = × = =
3 8 3 8 24 8
3 1 15 3 15 2 30 15 5 1
3 ÷1 = ÷ = × = = = =2
4 2 4 2 4 3 12 6 2 2

25. Make fractions using a
set of numbered cards,
and try some
multiplication and division
yourself.
Check them with a
calculator