The article investigates the role of third-order dispersion (TOD) and self-steepening in the propagation of higher-order optical solitons using accurate numerical simulations. It highlights how these higher-order effects influence soliton shape, center-shift, and lead to the decomposition of solitons into their constituents during propagation. The findings demonstrate that these effects are crucial for understanding nonlinear phenomena in optical fibers, especially for enhancing communication efficiency.

1. http://www.iaeme.com/IJARET/index.asp 54 editor@iaeme.com
International Journal of Advanced Research in Engineering and Technology
(IJARET)
Volume 7, Issue 1, Jan-Feb 2016, pp. 54-59, Article ID: IJARET_07_01_007
Available online at
http://www.iaeme.com/IJARET/issues.asp?JType=IJARET&VType=7&IType=1
Journal Impact Factor (2016): 8.8297 (Calculated by GISI) www.jifactor.com
ISSN Print: 0976-6480 and ISSN Online: 0976-6499
© IAEME Publication
___________________________________________________________________________
ACCURATE NUMERICAL SIMULATION OF
HIGHER ORDER SOLITON
DECOMPOSITION IN PRESENCE OF TOD
AND SELF- STEEPENING
RAJEEV SHARMA
Research Scholar, Mewar University, Rajasthan, India
HARISH NAGAR
AP, Mewar University, Rajashtan, India
G P SINGH
Govt. Dungar College Bikaner, Rajasthan, India
ABSTRACT
Generally, one considers only the group velocity dispersion (GVD) and
self-phase modulation (SPM) induced solitons in optical communication while
other higher order effects such as the third-order dispersion (TOD), self-
steepening, and stimulated Raman scattering are well thought-out only
perturbatively . In this article, we study the existence of the TOD and self-
steepening induced soliton solutions. The results have shown that, the
combination of the linear with nonlinear effects escort to new qualitative
feature as a shifting and the center-shift beside the deformation in the shape of
the soliton. To accomplish this purpose we used, the split-step Fourier
Method, in our simulations, that is broadly used to simulate numerical
solutions of the nonlinear Schrodinger equation.
Key words: Group Velocity Dispersion, Stimulated Raman Scattering, TOD,
Self-Steepening.
Cite this Article: Rajeev Sharma, Harish Nagar and G P Singh, Accurate
Numerical Simulation of Higher Order Soliton Decomposition In Presence of
TOD and Self- Steepening. International Journal of Advanced Research in
Engineering and Technology, 7(1), 2016, pp. 54-59.
http://www.iaeme.com/IJARET/issues.asp?JType=IJARET&VType=7&IType=1

2. Accurate Numerical Simulation of Higher Order Soliton Decomposition in Presence of TOD
and Self- Steepening
http://www.iaeme.com/IJARET/index.asp 55 editor@iaeme.com
1. INTRODUCTION
Optical solitons are the matter of broad theoretical and experimental studies
throughout the last four decades owing to their prospective applications in large
distance communication and all-optical ultrafast switching devices. The revolutionary
works of Hasegawa and Tappert, who predicted solitons theoretically, and Mollenauer
etal. [1] , who observed them experimentally, made solitons a practical instrument for
this cause. The solitons, confined-in-time optical pulse, evolve from a nonlinear
variation in the refractive index of the material, known as Kerr effect, stimulated by
the light intensity distribution. When the collective effects of the intensity-reliant
refractive index nonlinearity and the frequency-reliant pulse dispersion exactly
balance for one another, the pulse propagates without any change in its shape, being
self-trapped by the waveguide nonlinearity [2]. The transmission of picosecond
optical pulses in mono mode optical fibers is paragon by the totally integrable
nonlinear Schrodinger equation. This equation regulates the general condition of
dispersion propagation of a pulse envelope with a high carrier frequency in a weakly
nonlinear medium. even though the NLS equation includes only two substantial
effects, group velocity dispersion (GVD) and self-phase modulation (SPM), it
describes a range of nonlinear optical phenomena. Pivot on the relative signs of linear
group-velocity dispersion and nonlinearity stimulated self-phase modulation, they
coalesce to allow bright solitons [1], modulation instability and dark solitons. In order
to boost the bit rate in fiber optic communication systems to greater than 100 Gbit/s
for a single carrier frequency, it is obligatory to decrease the pulse width.
2. MODIFICATION IN NLSE
As light pulses become shorter, the standard NLS equation
i + +| 2
u = 0 (1)
Becomes inadequate. Thus extra terms which describe the effects of third-order
dispersion (TOD), self-steepening and intrapulse Raman scattering required to be
added to that equation
i + +| 2
u = -is (| 2
u) + u (2)
= (3)
s = 1/ T0 (4)
= TR/T0 (5)
3. SIMULATION AND RESULT
The propagation of optical signal along an optical fiber is described by the NLSE,
which has no analytical solutions except for some special cases. One can conclude
that a numerical approach is often necessary for understanding nonlinear effects in
dispersive media such as optical fibers [6-9]. Generally, a numerical approach is
required to solve all pulse-propagation problems in optical fibers. The most
commonly used method for solving these problems in nonlinear dispersive media is
SSFM [3].

3. Rajeev Sharma, Harish Nagar and G P Singh
http://www.iaeme.com/IJARET/index.asp 56 editor@iaeme.com
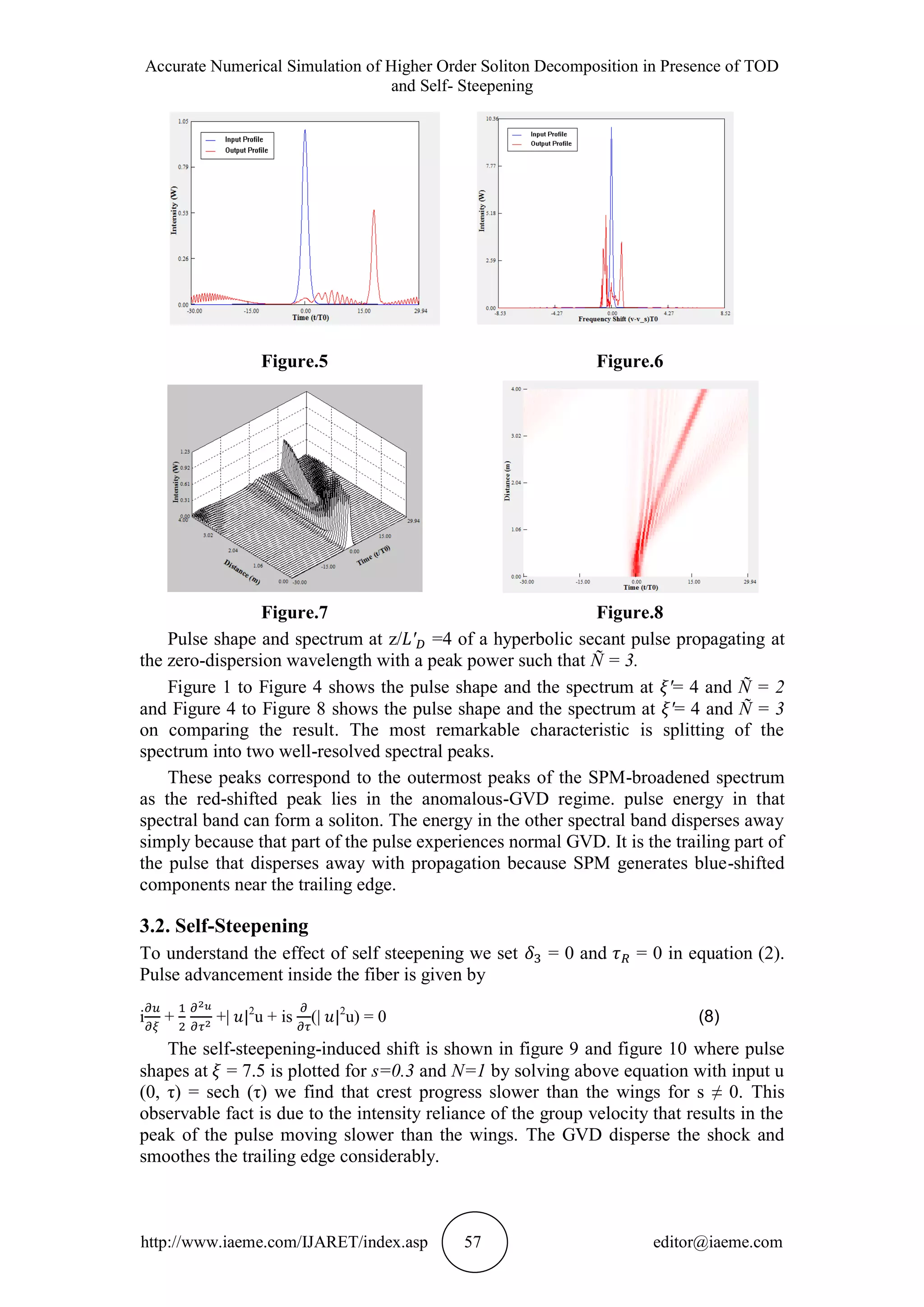
3.1. TOD
What happens if an optical pulse propagates at or near the zero-dispersion wavelength
of an optical fiber such that 2 is nearly zero [4]. Equation (2) cannot be used in this
case because the normalization scheme used for it becomes inappropriate.
Normalizing the propagation distance to = T0
3
/β3 through = z/ , we get
i - sgn (β3) + | 2
u = (6)
where u = ÑU with Ñ is defined by
Ñ
2
= = P0T0
3
/ (7)
The effect of TOD shown in figure 1 to figure 8 where pulse shapes at = 4 is are
plotted for Ñ = 2 and Ñ = 3 by solving above equation with input u (0,τ)= sech (τ)
Figure.1 Figure.2
Figure.3 Figure.4
Pulse shape and spectrum at z/ =4 of a hyperbolic secant pulse propagating at
the zero-dispersion wavelength with a peak power such that Ñ = 2.

4. Accurate Numerical Simulation of Higher Order Soliton Decomposition in Presence of TOD
and Self- Steepening
http://www.iaeme.com/IJARET/index.asp 57 editor@iaeme.com
Figure.5 Figure.6
Figure.7 Figure.8
Pulse shape and spectrum at z/ =4 of a hyperbolic secant pulse propagating at
the zero-dispersion wavelength with a peak power such that Ñ = 3.
Figure 1 to Figure 4 shows the pulse shape and the spectrum at = 4 and Ñ = 2
and Figure 4 to Figure 8 shows the pulse shape and the spectrum at = 4 and Ñ = 3
on comparing the result. The most remarkable characteristic is splitting of the
spectrum into two well-resolved spectral peaks.
These peaks correspond to the outermost peaks of the SPM-broadened spectrum
as the red-shifted peak lies in the anomalous-GVD regime. pulse energy in that
spectral band can form a soliton. The energy in the other spectral band disperses away
simply because that part of the pulse experiences normal GVD. It is the trailing part of
the pulse that disperses away with propagation because SPM generates blue-shifted
components near the trailing edge.
3.2. Self-Steepening
To understand the effect of self steepening we set = 0 and = 0 in equation (2).
Pulse advancement inside the fiber is given by
i + +| 2
u + is (| 2
u) = 0 (8)
The self-steepening-induced shift is shown in figure 9 and figure 10 where pulse
shapes at = 7.5 is plotted for s=0.3 and N=1 by solving above equation with input u
(0, τ) = sech (τ) we find that crest progress slower than the wings for s ≠ 0. This
observable fact is due to the intensity reliance of the group velocity that results in the
peak of the pulse moving slower than the wings. The GVD disperse the shock and
smoothes the trailing edge considerably.

5. Rajeev Sharma, Harish Nagar and G P Singh
http://www.iaeme.com/IJARET/index.asp 58 editor@iaeme.com
Figure.9 Figure.10
Pulse shapes for a fundamental soliton in the presence of self-steepening (s=0.3).
The result of self-steepening on higher-order solitons is leads to division of such
solitons into their constituents, a fact known as soliton decay as shown in simulation
results in figure.11 to figure.14
Figure.11 Figure.12
Decay of a second-order soliton N=2 induced by self-steepening (s=0.3).
Figure.13 Figure.14
Decay of a third-order soliton N=3 induced by self-steepening (s=0.3).
The second order soliton N=2 decompose into two solitons and third-order soliton
(N=3) decompose into three solitons whose peak heights are again in agreement with
inverse scattering theory.
4. CONCLUSION
In this paper, we have investigated through simulation two key phenomena’s one is
TOD and the other is self steepening on solitonic propogation. While studying TOD
The vital point to note is that, because of SPM-induced spectral broadening, the input
pulse does not actually propagate at the zero-dispersion wavelength even if β2 =0
initially. In effect, the pulse creates its own β2j through SPM. Simulation result shows

6. Accurate Numerical Simulation of Higher Order Soliton Decomposition in Presence of TOD
and Self- Steepening
http://www.iaeme.com/IJARET/index.asp 59 editor@iaeme.com
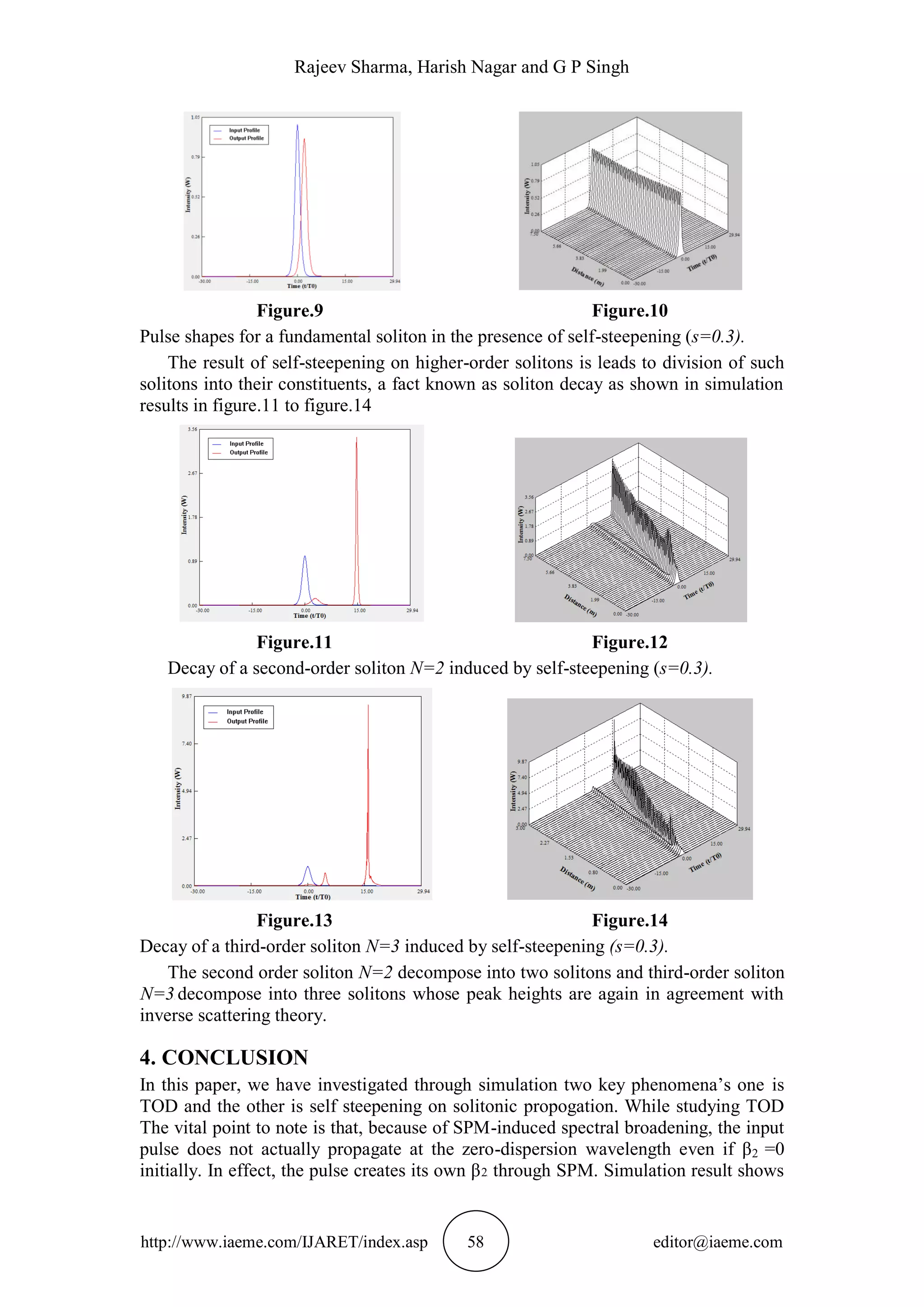
that for Ñ >1, a “sech” pulse progress over a length ~ 10/ Ñ
2
 into a soliton that
contains about half of the pulse energy. The remaining energy is carried by an
wavelike structure near the trailing edge that disperses away with propagation. The
effect of self-steepening on higher-order solitons is significant in that it leads to
disintegration of such solitons into their constituents.
REFRENCES
[1] G. P. Agrawal Nonlinear Fiber Optics, Academic Press (2001).
[2] K. Ohkuma, Y.H. Ichikawa, and Y. Abe, Soliton propagation along optical
fibers, Opt. Lett., 12, 516-518, 1987.
[3] S. Siddamal, R. Banakar, and B. Jinaga, Split Step Method in the Analysis
and Modeling of Optical Fiber Communication System, Springer Verlag
Heidelberg, 254-261, 2011.
[4] P. K. Wai, C. R. Menyuk, Y. C. Lee, and H. H. Chen, Nonlinear pulse
propagation in the neighborhood of the zero-dispersion wavelength of
monomode optical fibers, Opt. Lett. 11, 464-466, 1986.
[5] S.R. Clarke, R.H.J. Grimshaw, and B.A. Malomed, Soliton formation from a
pulse passing the zero dispersion point in a nonlinear Schödinger equation,
Phys. Rev. E 61, 5794-5801, 2000.
[6] E. A. Golovchenko, E. M. Dianov, A. M. Prokhorov, and V. N. Serkin,
Decay of optical solitons, JETP Lett. 42, 87-91, 1985.
[7] Kuochou Tai and Akira Hasegawa, Fission of optical solitons induced by
stimulated Raman Effect, Opt. Lett. 13, 392-394, 1988.
[8] Jing Wang, Shanshan Wang, Xiaoliang Chu, Meiling Sun, Numerical Study
on Optical Solitons Transmission System with 40 Gbit/s in the Photonic
Crystal Fiber, Optics and Photonics Journal, 3,141-146, 2013.
[9] Elham Jasim Mohammad and Gaillan H. Abdullah, Soliton Optical Fibers
Super continuum Generation near The Zero Dispersion. International Journal
of Industrial Engineering research and Development 4(1), 2013, pp. 52-58.
[10] Tarnveer Kaur, Kamaljit Singh Bhatia, and Kulwinder Singh, Factors
Affecting Higher Order Solitons in Soliton Transmission, International
Conference on Innovations in Engineering and Technology (ICIET'2013)
Dec. 25-26, 2013 Bangkok.