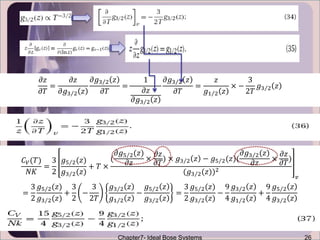
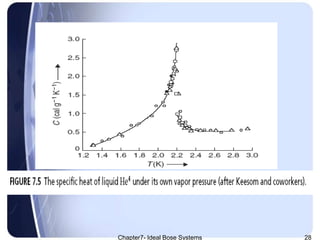
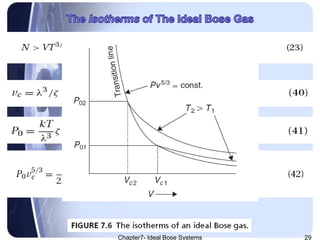
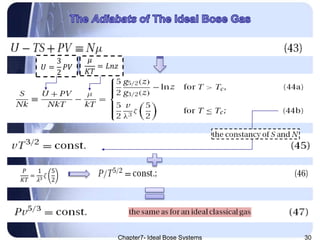
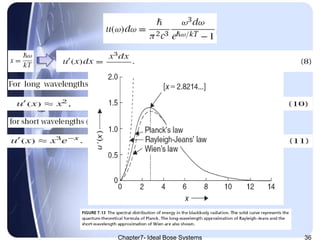
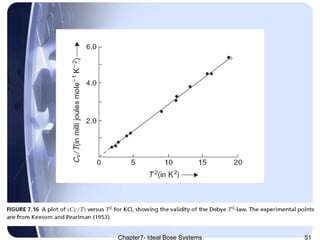
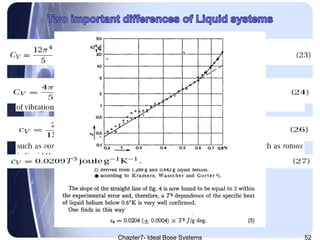
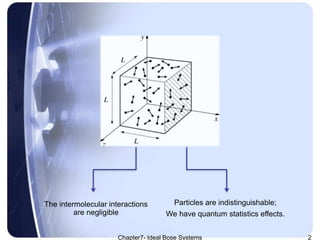
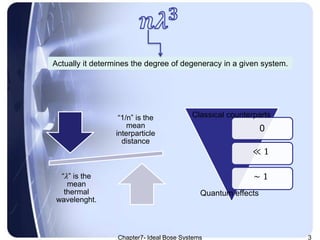
The document discusses Ideal Bose systems, emphasizing the negligible intermolecular interactions and the indistinguishability of particles under quantum statistical mechanics. It explains various equations and concepts such as mean interparticle distance, thermal wavelength, and particle excitations, detailing how these factors influence the behavior of the systems. Additionally, the document presents mathematical formulations related to pressure, volume, and temperature dynamics in the context of Bose systems.













![Chapter7- Ideal Bose Systems 24
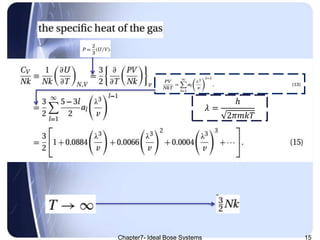
𝐶 𝑉
𝑁𝐾
=
1
𝑁𝐾
𝜕𝑈
𝜕𝑇 𝑁,𝑉
=
3
2
𝜕
𝜕𝑇
𝑃𝑉
𝑁𝐾 𝑣
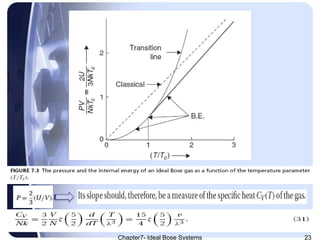
𝑃 𝑇 =
𝐾𝑇
𝜆3
𝜁
5
2
𝐶 𝑉
𝑁𝐾
=
3
2
[
𝜕
𝜕𝑇
𝐾𝑇
𝜆3
𝜁
5
2
×
𝑉
𝑁𝐾
] 𝑣 =
3
2
𝑉
𝑁
𝜁
5
2
×
𝑑
𝑑𝑇
𝑇
𝜆3
=
3
2
𝑣𝜁
5
2
×
𝑑
𝑑𝑇
𝑇
5
2
2𝜋𝑚𝐾
3
2
ℎ3
=
3
2
𝑣𝜁
5
2
×
5
2
×
1
𝜆3 =
15
4
𝜁
5
2
𝑣
𝜆3](https://image.slidesharecdn.com/idialbosesystems-180921093401/85/Ideal-Bose-Systems-24-320.jpg)