The document is a project report on vibration analysis of a wheelchair. It analyzes the wheelchair as a single degree of freedom (SDOF) system, then a two degree of freedom (TDOF) system, and finally as a multi degree of freedom (MDOF) system to account for increased complexity. Key steps include developing models of the wheelchair as a SDOF system, calculating natural frequency and response, then expanding the analysis to a TDOF and MDOF model considering additional masses and degrees of freedom. Graphs and equations are provided to analyze vibration properties at each level of complexity.

1. 1
In the fulfill of the requirement of the
Vibration of machines and structures
(MECH 6311)
Summer 15
A project report on
Vibration analysis of wheelchair
Submitted to
Dr. R Ganesan, Ph.D., Eng
By
Aniruddhsinh barad [7180217]
Bhoomirajsinh barad [7180225]
Viral kale [7677871]
Department of Mechanical and Industrial Engineering
Faculty of Engineering & Computer Science

2. 2
Abstract
In this project, we concerned the vibration analysis of half portion of
the wheel chair. First we considered the different properties of the system and get
the values for all parameters from the real life examples. Then, we considered the
whole system as one equivalent SDOF model system and developed one
elementary model and we calculated the all the parameters and responses of
system. In the next step we analyzed magnification factor and transmissibility of
the system. At last the whole system is studied for multi degree of freedom system
for more complexity.

3. 3
Index
1. Vibration model of wheel chair…………………………………4
2. SDOF system of wheelchair …………………………………….6
3. Two DOF system analysis……………………………………...11
4. MDOF system analysis…………………………………………13
5. References……………………………………………………….20
Figures
1. Wheelchair suspension system….………………………………4
2. SDOF suspension system………….…………………………….6
3. Two DOF suspension system……...………………………...…11
4. MDOF suspension system...……………………………………13

4. 4
1. Vibration model of wheel chair:
Fig.1 Wheelchair suspension system

5. 5
Contractions:
 Mh = mass of human
 Mf = mass of frame
 Mu = mass of tyre(wheel)
 Kc = stifness of tyre
 Kc = stifness of cushion
 Kf = stifness of frame suspension
 Cf = damping of frame
 Cc = damping of cushion
 v = velocity
 ξ = Damping Ratio
Data:
 Mh = 50 kg
 Mf = 13 kg
 Mu = 1.2 kg
 Ku = 56 ∗ 104 N
m
 Kc = 1.161 ∗ 104 N
m
 Kf = 104 N
m
 Kcf = 2.16 ∗ 104 N
m
 Cf = 150
Ns
m
 Cc = 115
Ns
m
 Ccf = 265
Ns
m
 v = 0.5
m
s
 ξ = 0(no damping)
y = 0.01sin(
2πvt
2.5
)
= 0.01sin(
2π ∗ 0.5 ∗ t
2.5
)
ω = (
2πv
2.5
)

6. 6
= (
2π ∗ 0.5
2.5
)
∴ ω = 1.256 rad/sec
2. SDOF system of wheelchair:
Fig.2 SDOF suspension system
Kinetic energy:
T =
1
2
Muẋ 2
t+
1
2
Mhfẋ 2
t
=
1
2
(Mu + Mhf)ẋ 2
t

7. 7
Meq = (Mu + Mhf)
= (1.2 + 63)
∴ Meq = 64.2 kg
Potential energy:
U =
1
2
Kuẋ2
t +
1
2
Kcfẋ 2
t
=
1
2
(Ku + Kcf)ẋ2
t
Keq = (Ku + Kcf)
Keq = 2.16 ∗ 104
N
m
Damping:
C = ∫ Ccf xt
2̇
Ceq = Ccf
Ceq = 265 Ns/m
Natural frequency:
ωn = √
Keq
Meq
= √
58.16 ∗ 104
64.2
ωn = 95.18 rad/sec

8. 8
Frequency ratio:
r =
ω
ωn
=
1.256
95.18
r = 0.01319
Damped frequency:
ωd = ωn√1 − ξ2
ωn = 95.15 rad/sec
Critical Damping ratio:
Cc =2Meqωn
=2*64.2*95.18
Cc = 1.2 ∗ 104
Ns/m
Damping ratio:
ξ =
C
Cc
ξ =0.022
Amplitude of Vibration:
X
Y
= √
1 + (2ƺr)2
(1 − r2)2 + (2ƺr)2

9. 9
Neglect damping,
X
Y
=
1
1 − r2
X
0.01
=
1
1 − 0.013192
X = xu=0.01000174 m
Magnification:
MF =
1
√(1 − r2)2 + (2ξr)2
MF = 1.00356
Case-1
For minimum magnification r = 1.5,
(𝑇𝑅) =
𝑋
𝑌
= √
1 + (2ƺ𝑟)2
(1 − 𝑟2)2 + (2ƺ𝑟)2
(TR) = 0.80
MFmin =
1
√(1 − r2)2 + (2ξr)2
MFmin = 0.799
Case-2
For maximum magnification ξ=0.022
MFmax =
1
2ξ√1 − ξ2
MFmax = 22.732
rmax = √1 − 2ξ2
rmax = 1.0009

10. 10
Free undammed condition:
∴ ξ = 0, F(t) = 0
Meqẍ + Ceqẋ + Keqx = 0
Total response
x(t) =
ẋ(0)
ωn
sinωnt + x(0)cosωnt
x(t) =
ẋ(0)
95.18
sin95.18t + x(0)cos95.18t
For damped response:
F(t)=0
Meqẍ + Ceqẋ + Keqx = F(t)
Meqẍ + Ceqẋ + Keqx = 0
Total Response:
x(t) = e−ξωnt
(
ẋ(0) + ξωnx(0)
ωd
sinωdt + x(0)cosωdt)
x(t) = e−2.09t
(
ẋ(0) + 2.09x(0)
95.15
sin95.15t + x(0)cos95.15t)
For harmonic response:
Meqẍ + Ceqẋ + Keqx = F0sinωt
64.2ẍ + 265ẋ + 2.16 ∗ 104
x = F0sinωt
Total harmonic response
x(t) =
F0
K
(
sin(ωt − ∅)
√(1 − r2)2 + (2ξr)2
+ Xe−ξωnt
(sin(ωdt + ∅)

11. 11
3. Two degree of freedom system [TDOF]:
Fig.3 Two DOF suspension system
Mu 𝑥 𝑢̈ = −Kuxu − Kcf(xu − xhf) − Ccf(𝑥 𝑢̇ − 𝑥ℎ𝑓)̇
Mhf 𝑥ℎ𝑓̈ = Kcf(xu − xhf) + Ccf(𝑥 𝑢̇ − 𝑥ℎ𝑓)̇
[
Mu 0
0 Mhf
] [
𝑥 𝑢̈
𝑥ℎ𝑓̈ ] + [
Ccf −Ccf
−Ccf Ccf
] ⌈
𝑥 𝑢̇
𝑥 𝑐𝑓̇ ⌉ + [
(Ku + Kcf) −Kcf
−Kcf Kcf
] ⌈
xu
xhf
⌉ = 0
[
xu
xhf
] = [
A1
A2
] 𝑠𝑖𝑛𝜔𝑡
⌈
𝑥 𝑢̇
𝑥 𝑐𝑓̇ ⌉ = 𝜔 [
A1
A2
] 𝑐𝑜𝑠𝜔𝑡
[
𝑥 𝑢̈
𝑥ℎ𝑓̈ ] = −𝜔2
[
A1
A2
] 𝑠𝑖𝑛𝜔𝑡

12. 12
−𝜔2
𝑠𝑖𝑛𝜔𝑡 [
Mu 0
0 Mhf
] [
A1
A2
] + 𝜔𝑐𝑜𝑠𝜔𝑡 [
Ccf −Ccf
−Ccf Ccf
] ⌈
A1
A2
⌉
+ 𝑠𝑖𝑛𝜔𝑡 [
(Ku + Kcf) −Kcf
−Kcf Kcf
] ⌈
A1
A2
⌉ = [
0
0
]
−𝜔2
[
1.2 0
0 63
] [
A1
A2
] + 𝜔 [
265 −265
−265 265
] ⌈
A1
A2
⌉
+ [
581600 −21600
−21600 21600
] ⌈
A1
A2
⌉ = [
0
0
]
𝜔2
[−1.2𝜔2
+ 265𝜔 + 581600 −265𝜔 + 21600
−265𝜔 − 21600 −63𝜔2
+ 265𝜔 + 21600
] ⌈
A1
A2
⌉ = [
0
0
]
Solving the matrix we get the Eigen Values,
𝜆1 = 4.8468 ∗ 105
𝜆2 = 0.0033 ∗ 105
Using the Eigen values, we find out the Eigen vectors as below,
∅1 = {
0.999
−0.0007
}
∅2 = {
0.037
0.999
}

13. 13
4. MDOF system of wheelchair:
Fig.4 MDOF suspension system
Kinetic energy,
T=
1
2
𝑀 𝑢 𝑋̇2
𝑢+
1
2
𝑀ℎ𝑓 𝑋̇2
ℎ𝑓+
1
2
𝐽 𝑜Ɵ̇ 2
Potential energy,
U=
1
2
𝐾 𝑢 𝑋2
𝑢+
1
2
𝐾 𝑐𝑓
2
(𝑋 𝑢 − (𝑋ℎ𝑓 − 𝑙1Ɵ))2
+
1
2
𝐾 𝑐𝑓
2
(𝑋 𝑢 − (𝑋ℎ𝑓 + 𝑙2Ɵ))2

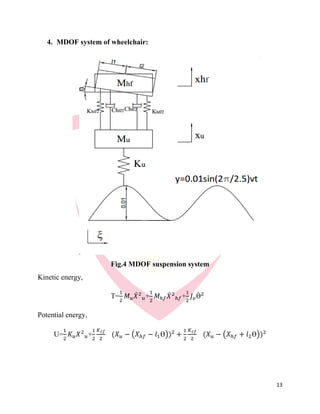
14. 14
Equation of motion,
1. 𝑞𝑖=𝑋 𝑢
𝑑
𝑑𝑡
(
𝜕𝑇
𝜕𝑋 𝑢
)= 𝑀 𝑢 𝑋̈ 𝑢
𝜕 𝑢
𝜕𝑥 𝑢
=𝐾 𝑢 𝑋 𝑢+
𝐾 𝑐𝑓
2
(𝑋 𝑢 − (𝑋ℎ𝑓 − 𝑙1Ɵ))+
𝐾 𝑐𝑓
2
(𝑋 𝑢 − (𝑋ℎ𝑓 + 𝑙2Ɵ))
𝑴 𝒖 𝑿̈ 𝒖+𝑿 𝒖(𝑲 𝒖 + 𝑲 𝒄𝒇)-𝑲 𝒄𝒇 𝑿 𝒉𝒇+
𝑲 𝒄𝒇
𝟐
Ɵ(𝒍 𝟏 − 𝒍 𝟐)=0
Now, 𝑞1̇ =𝑋ℎ𝑓
𝑑
𝑑𝑡
(
𝜕𝑇
𝜕𝑋̇ 𝐻𝐹
)= 𝑀ℎ𝑓 𝑋̈2
ℎ𝑓
𝜕𝑈
𝜕𝑋ℎ𝑓
=−
𝐾 𝑐𝑓
2
(𝑋 𝑢 − 𝑋ℎ𝑓 + 𝑙1Ɵ)- −
𝐾 𝑐𝑓
2
(𝑋 𝑢 − 𝑋ℎ𝑓 − 𝑙2Ɵ)
𝑴 𝒉𝒇 𝑿̈ 𝟐
𝒉𝒇 −
𝑲 𝒄𝒇
𝟐
(𝑿 𝒖 − 𝑿 𝒉𝒇 + 𝒍 𝟏Ɵ)- −
𝑲 𝒄𝒇
𝟐
(𝑿 𝒖 − 𝑿 𝒉𝒇 − 𝒍 𝟐Ɵ)=0
𝑓𝑜𝑟, 𝑞𝑖 =Ɵ
(
𝜕𝑇
𝜕𝜃
) = 𝐽˳𝜃̈
𝑑
𝑑𝑡
𝜕𝑈
𝜕𝜃
=
−𝐾𝑐𝐹
2
𝑙1(𝑥𝑢 − 𝑥ℎ𝐹 + 𝑙1𝜃) +
𝐾𝑐𝐹
2
𝑙2 (𝑥𝑢 − 𝑥ℎ𝐹 − 𝑙2𝜃)
𝑱˳𝜽̈ +
𝑲𝒄𝑭
𝟐
𝒙𝒖 (𝒍𝟐 − 𝒍𝟏) +
𝑲𝒄𝑭
𝟐
𝒙𝒉𝑭(𝒍𝟏 − 𝒍𝟐) −
𝑲𝒄𝑭
𝟐
(𝒍𝟏 𝟐
+ 𝒍𝟐 𝟐
)𝜽
[
𝑚 𝑢 0 0
0 𝑚ℎ𝑓 0
0 0 𝑗𝑜
] {
𝑥̈ 𝑢
𝑥̈ℎ𝑓
Ɵ̈
}+
[
𝑘 𝑢 + 𝑘 𝑐𝑓 −𝑘 𝑐𝑓
𝑘 𝑐𝑓(𝑙1−𝑙2)
2
−𝑘 𝑐𝑓 𝑘 𝑐𝑓
𝑘 𝑐𝑓(𝑙2−𝑙1)
2
𝑘 𝑐𝑓(𝑙1−𝑙2)
2
𝑘 𝑐𝑓(𝑙2−𝑙1)
2
−𝑘 𝑐𝑓(𝑙12+𝑙22)
2 ]
{
𝑋𝑢
𝑋ℎ𝑓
Ɵ
} = {
0
0
0
}

15. 15
Now we take
{
𝑋𝑢
𝑋ℎ𝑓
Ɵ
} = {
𝐴𝑢
𝐴ℎ𝑓
Ɵℎ𝑓
} sinωt
-ω2
sin ωt[
𝑚 𝑢 0 0
0 𝑚ℎ𝑓 0
0 0 𝑗𝑜
] {
𝑋𝑢
𝑋ℎ𝑓
Ɵ
} +sin
ωt
[
𝑘 𝑢 + 𝑘 𝑐𝑓 −𝑘 𝑐𝑓
𝑘 𝑐𝑓(𝑙1−𝑙2)
2
−𝑘 𝑐𝑓 𝑘 𝑐𝑓
𝑘 𝑐𝑓(𝑙2−𝑙1)
2
𝑘 𝑐𝑓(𝑙1−𝑙2)
2
𝑘 𝑐𝑓(𝑙2−𝑙1)
2
−𝑘 𝑐𝑓(𝑙12+𝑙22)
2 ]
{
𝑋𝑢
𝑋ℎ𝑓
Ɵ
} = {
0
0
0
}
-ω2
[
1.2 0 0
0 63 0
0 0 0.5419
] {
𝑋𝑢
𝑋ℎ𝑓
Ɵ
} +
[
581600 −2.16 ∗ 104
0
−2.16 ∗ 104
2.16 ∗ 104
0
0 0 −111.48
] {
𝑋𝑢
𝑋ℎ𝑓
Ɵ
}={
0
0
0
}
Assume, ω2
=⅄
[
581600 − 1.2⅄ −2.16 ∗ 104
0
−2.16 ∗ 104
2.16 ∗ 104
− 63⅄ 0
0 0 −111.48 − 0.5419⅄
] {
𝑋𝑢
𝑋ℎ𝑓
Ɵ
}={
0
0
0
}
⅄=[
4.84679 0 0
0 0.00330115 0
0 0 −0.0205720
] 105
⅄1=4.84679*105
⅄2=0.00330115*105

16. 16
⅄3=-0.0205720*105
𝜔3𝑛=0.0+45.3341i
𝜔1𝑛=696.19 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
𝜔2𝑛=18.16 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
𝜔3𝑛=45.35 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
Eigen vectors,
∅1 = {
0.9999
−0.000707
0
}
∅2 = {
0.0371386
0.931012
0
}
∅3 = {
0
0
1.000
}
Modal matrix,
P=[
0.9999 0.0371386 0
−0.000707 0.9931012 0
0 0 1.000
]
𝑃 𝑇
=[
0.9999 −0.000707 0
0.0371386 0.9931012 0
0 0 1.000
]

17. 17
Generalizes mass,
𝑃 𝑇
𝑀𝑃=[
1.2 0 0
0 62.9147 0
0 0 0.054190
]
Generalized stiffness,
𝑃 𝑇
𝐾𝑃=[
5.8163 0 0
0 0.2076911 0
0 0 −0.00111480
]
Amplitude ratio
Y=0.01,
ƺ=0.022
𝐹𝑜𝑟, 𝑟=
𝜔
𝜔 𝑛1
=1.8*10−3
𝑋
𝑌
=√
1+(2ƺ𝑟)2
(1−𝑟2)2+(2ƺ𝑟)2
𝑋
𝑌
=√
1+(2∗0.022∗1.8∗10−3)2
(1−1.8∗10−32
)
2
+(2∗0.022∗1.8∗10−3)2
X=0.01 m
𝐹𝑜𝑟, 𝑟=
𝜔
𝜔 𝑛2
=0.069
𝑋
𝑌
=√
1+(2ƺ𝑟)2
(1−𝑟2)2+(2ƺ𝑟)2
𝑋
𝑌
=√
1+(2∗0.022∗0.069)2
(1−0.0692)2+(2∗0.022∗0.069)2
X=0.01 m

18. 18
Frequency ratio:
𝐹𝑜𝑟, 𝑟=
𝜔
𝜔 𝑛3
=0.027
Y=0.00989m
𝑋
𝑌
=√
1+(2ƺ𝑟)2
(1−𝑟2)2+(2ƺ𝑟)2
𝑋
𝑌
=√
1+(2∗0.022∗0.027)2
(1−0.0272)2+(2∗0.022∗0.027)2
X=0.01 m
Now we consider the force 𝑓0 sinωt
Where 𝑓0=500 N
F=[
0
𝑓0 sin ωt
0
]
F=[
0
500
0
] sin ωt
𝑃 𝑇
F=[
0.9999 −0.000707 0
0.0371386 0.9931012 0
0 0 1.000
] [
0
500
0
] sin ωt
𝑃 𝑇
F=[
18.569
499.65
0
] sin ωt

19. 19
Assume
ƺ=0.05
𝑓𝑜𝑟 𝜔1𝑛=696.19 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
𝑐 𝑐=1670.55 𝑁𝑆
𝑚⁄
C=83.54 𝑁𝑆
𝑚⁄
1.2𝒙̈ +83.54𝒙̇ +5.8163*𝟏𝟎 𝟓
𝒙=18.569 sin ωt
Total response,
𝑥(𝑡) = 𝑒−34.81𝑡
(
𝑥̇(0)+34.81𝑥(0)
695.32
𝑠𝑖𝑛695.32𝑡 + 𝑥(0)𝑐𝑜𝑠695.32𝑡) +
(3.19*105
sin(1.265𝑡 − 𝜙))
𝑓𝑜𝑟 𝜔12=18.16 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
ƺ=0.05
𝑐 𝑐=2285.06 𝑁𝑆
𝑚⁄
C=114.25 𝑁𝑆
𝑚⁄
62.9147𝒙̈ +114.25𝒙̇ +0.2061*𝟏𝟎 𝟓
𝒙=499.65 sin ωt
𝑥(𝑡) = 𝑒−18.14𝑡
(
𝑥̇(0)+18.14𝑥(0)
18.14
𝑠𝑖𝑛18.14𝑡 + 𝑥(0)𝑐𝑜𝑠18.14𝑡) +
(0.024sin(1.265𝑡 − 𝜙))
𝑓𝑜𝑟 𝜔13=45.35 𝑟𝑎𝑑
𝑠𝑒𝑐⁄
ƺ=0.05
𝑐 𝑐=4.915 𝑁𝑆
𝑚⁄

20. 20
C=0.2457 𝑁𝑆
𝑚⁄
0.5419𝒙̈ +0.2457𝒙̇ +0.001148*𝟏𝟎 𝟓
𝒙=0
𝑥(𝑡) = 𝑒−2.26𝑡
(
𝑥̇(0) + 2.26𝑥(0)
45.29
𝑠𝑖𝑛2.26𝑡 + 𝑥(0)𝑐𝑜𝑠2.26𝑡)

21. 21
References:
5. http://www.rehab.research.va.gov/jour/11/483/pdf/akins.pdf
6. Damping characteristics of seat cushion materials for tractor ride comfort.
By (C.R.Mehta, V.K.Tiwari)