Downloaded 11 times
![汎化についての経験則
• broad minima > sharp minima
• 曲率の小さいminima(broad minima)は大きいminima(sharp minima)
より汎化する。[Chaudhari et al. (2016)]
• ランダムデータから得られた解はヘッセ行列の最大固有値が大きい。
[Krueger et al. (2017)]
• しかしパラメタの取り方を変えれば汎化性能の高いsharp minimaも作
れる。[Dinh et al. (2017)]](https://image.slidesharecdn.com/0123bayes-180123100528/85/A-Bayesian-Perspective-on-Generalization-and-Stochastic-Gradient-Descent-5-320.jpg)
![SGDと汎化
• ベイズ証拠を最大化するためにベイズではノイズを加える
[Mandt et al., 2017; Welling & Teh, 2011]
• SGDでも同じことが起こっていると考えられる
• バッチサイズを大きくするとノイズが減るので汎化性能が下がる](https://image.slidesharecdn.com/0123bayes-180123100528/85/A-Bayesian-Perspective-on-Generalization-and-Stochastic-Gradient-Descent-18-320.jpg)
Uploaded byRyutaro Yamauchi
[論文解説]A Bayesian Perspective on Generalization and Stochastic Gradient Descent
2018/01/23 arXivTimes勉強会
![[DL輪読会]A Bayesian Perspective on Generalization and Stochastic Gradient Descent](https://cdn.slidesharecdn.com/ss_thumbnails/20171106dl2-171108033614-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Deep Learning 第5章 機械学習の基礎](https://cdn.slidesharecdn.com/ss_thumbnails/deeplearning5-180601021956-thumbnail.jpg?width=640&height=640&fit=bounds)
![[PRML] パターン認識と機械学習（第3章：線形回帰モデル）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter3-171003081954-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Scalable Training of Inference Networks for Gaussian-Process Models](https://cdn.slidesharecdn.com/ss_thumbnails/mainslideshare1-190927025239-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DeepLearning論文読み会] Dataset Distillation](https://cdn.slidesharecdn.com/ss_thumbnails/datasetdistillation-181114165952-thumbnail.jpg?width=640&height=640&fit=bounds)
![[論文解説]Unsupervised monocular depth estimation with Left-Right Consistency](https://cdn.slidesharecdn.com/ss_thumbnails/unsupervisedmonoculardepthestimation-170809092538-thumbnail.jpg?width=640&height=640&fit=bounds)
[論文解説]A Bayesian Perspective on Generalization and Stochastic Gradient Descent
- 1. A Bayesian Perspectiveon Generalization and Stochastic Gradient Descent arXivTimes勉強会 山内隆太郎
- 2. 本日紹介する論文 • A BayesianPerspective on Generalization and Stochastic Gradient Descent • Samuel L. Smith, Quoc V. Le • https://arxiv.org/abs/1710.06451
- 3.
- 4. 背景 • Zhang etal. (2016) • DNNはランダムにラベル付けされたデータを丸暗記できる • ランダムデータを過学習可能なモデルが正しいデータでは汎化すると いう事実は、モデルの複雑さを評価する従来の汎化理論では説明でき ない • 正しいデータにはランダムデータにはない“自然さ”がある？
- 5. 汎化についての経験則 • broad minima> sharp minima • 曲率の小さいminima(broad minima)は大きいminima(sharp minima) より汎化する。[Chaudhari et al. (2016)] • ランダムデータから得られた解はヘッセ行列の最大固有値が大きい。 [Krueger et al. (2017)] • しかしパラメタの取り方を変えれば汎化性能の高いsharp minimaも作 れる。[Dinh et al. (2017)]
- 6. Contributions 1. Zhangの結果はDeep Learningに特有ではなく、より小さな 線形モデルでも観察できる。 この現象は“ベイズ証拠”を評価することで説明できる。 2.SGDが汎化するのはノイズによる。このノイズの 大きさは𝑔 ≈ 𝜖𝑁 𝐵 に 従う。ノイズの大きさには最適値が存在し、 したがって最適なバッチサイズは学習率𝜖および学習データサ イズ𝑁に比例する。
- 7. 論文の流れ 1. ベイズ証拠の紹介 • モデルパラメタで周辺化したデータの尤度 𝑃𝑦 𝑥 ; 𝑀 = ∫ 𝑑𝑤 𝑃 𝑦 𝑤, 𝑥 ; 𝑀) 𝑃(𝑤; 𝑀) • 学習データが事前分布をどれだけ更新しなくてはならないかを意味す る（ベイズ証拠が大きいほど少ない更新で済む） 2. 線形モデルでベイズ証拠を観察し、汎化性能と関係している ことを示す。 • 学習セットだけで汎化性能を予測できる！ 3. SGDとノイズスケーリング則
- 8. ベイズモデル比較 • L2正則化付き交差エントロピー最小化は、ガウス分布を事前分布と したベイズ推定として解釈できる。 𝑃 𝑤𝑦 , 𝑥 ; 𝑀) = 𝑃 𝑦 𝑤, 𝑥 ; 𝑀 𝑃 𝑤; 𝑀 𝑃 𝑦 𝑥 ; 𝑀 ∝ 𝑃 𝑦 𝑤, 𝑥 ; 𝑀 𝑃 𝑤; 𝑀 ここで 𝑃 𝑦 𝑤, 𝑥 ; 𝑀 = 𝑖 𝑃 𝑦𝑖 𝑤, 𝑥𝑖; 𝑀 = 𝑒−𝐻(𝑤;𝑀) 𝑃 𝑤; 𝑀 = 𝜆 2𝜋 𝑒− 𝜆𝑤2 2 に注意すると、 ※ただし𝐻(𝑤; 𝑀) = − 𝑖 ln(𝑃(𝑦𝑖|𝑤, 𝑥𝑖; 𝑀))
- 9. ベイズモデル比較（2） 𝑃 𝑤 𝑦, 𝑥 ; 𝑀) ∝ 𝑃 𝑦 𝑤, 𝑥 ; 𝑀 𝑃 𝑤; 𝑀 = 𝜆 2𝜋 𝑒 − 𝐻 𝑤;𝑀 +𝜆 𝑤2 2 𝐶 𝑤; 𝑀 = 𝐻 𝑤; 𝑀 + 𝜆 𝑤2 2 はL2正則化付き交差エントロピー最小化のコ スト関数 よって𝐶 𝑤; 𝑀 を最小化する𝑤0は𝑃 𝑤 𝑦 , 𝑥 ; 𝑀)を最大化する。 ベイズ推定の場合、予測の際には 𝑃 𝑦𝑡 𝑥𝑡, 𝑥 , 𝑦 ; 𝑀 = ∫ 𝑑𝑤 𝑃 𝑦𝑡 𝑤, 𝑥𝑡; 𝑀) 𝑃(𝑤| 𝑦 , 𝑥 ; 𝑀) を解く必要があるが、この積分は𝑤0周りが支配的だと考えられるので、 𝑃 𝑦𝑡 𝑥𝑡; 𝑀 ≈ 𝑃 𝑦𝑡 𝑤0, 𝑥𝑡; 𝑀 と近似する。
- 10. ベイズモデル比較（3） • ベイズモデル比較：モデル𝑀1と𝑀2の尤もらしさを比較 𝑃 𝑀1𝑦 , 𝑥 𝑃 𝑀2 𝑦 , 𝑥 = 𝑃 𝑦 𝑥 ; 𝑀1 𝑃 𝑦 𝑥 ; 𝑀2 𝑃 𝑀1 𝑃(𝑀2) • §3ではランダムな出力を返すモデルとのベイズモデル比較を 行う • 本論文ではprior ratio=1と仮定 evidence ratio prior ratio
- 11. ベイズモデル比較（4） 𝑃 𝑦 𝑥; 𝑀 = 𝑑𝑤 𝑃 𝑦 𝑤, 𝑥 ; 𝑀) 𝑃(𝑤; 𝑀) = 𝜆 2𝜋 ∫ 𝑑𝑤 𝑒−𝐶(𝑤;𝑀) この積分も𝑤0が支配的だと考えられるので、 𝐶 𝑤; 𝑀 ≈ 𝐶 𝑤0 + 1 2 𝐶′′ 𝑤0 𝑤 − 𝑤0 2 とテーラー展開すると（𝐶’ 𝑤0 ≈ 0に注意） 𝑃 𝑦 𝑥 ; 𝑀 ≈ exp − 𝐶 𝑤0 + 1 2 ln 𝐶′′ 𝑤0 𝜆 と近似できる。 これは𝐶(𝑤0)および𝑤0における𝐶(𝑤)の曲率が小さい（broad minima）ときベ イズ証拠が大きくなることを意味する。
- 12. ベイズモデル比較（5） • これまでモデルが一変数の場合を考えてきたが、これを多変数 に拡張すると 𝑃 𝑦𝑥 ; 𝑀 = 𝜆 𝑃 2 ∇2 𝐶 𝑤0 𝑤0 1 2 𝑒−𝐶 𝑤0 ≈ exp − 𝐶 𝑤0 + 1 2 𝑖=1 𝑃 ln( 𝜆 𝑖 𝜆 ) 𝑃はモデルのパラメタ数 𝜆𝑖は∇2 𝐶(𝑤0)の固有値 • Occam factorはパラメタの摂動に対する安定性を意味する • パラメタの取り方を変えて曲率を変えてもOccam factorは一定 Occam factor
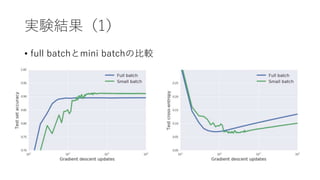
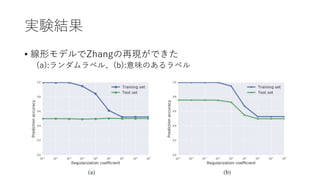
- 13. 実験 • 線形モデルでベイズ証拠を計算する モデル：200weights and1 bias Regularization Coefficient（λ）を変化させながらベイズ証拠と精度の 関係を見る • データセット 𝑥 :正規分布からサンプリングされた200次元のベクトル 𝑦 : 𝑦𝑖 = 1 𝑥𝑖 > 0 0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 学習セット：200 examples 評価セット：10000 examples
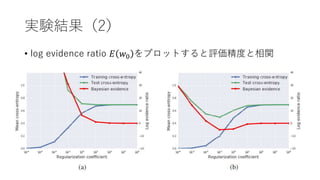
- 14. 実験（2） • ランダム出力を返すモデル𝑃 𝑦𝑥 ; 𝑁𝑈𝐿𝐿 = 1 𝑛 𝑁 = 𝑒−𝑁𝑙𝑛(𝑛) とベイズ証拠を比較 𝑃 𝑦 𝑥 ; 𝑀 𝑃 𝑦 𝑥 ; 𝑁𝑈𝐿𝐿 = 𝑒−𝐸(𝑤0) ただし𝐸 𝑤0 = 𝐶 𝑤0 + 1 2 𝑖=1 𝑃 ln( 𝜆𝑖 𝜆 ) − 𝑁𝑙𝑛(𝑛) • 𝐸 𝑤0 <0のときランダムよりマシ
- 15.
- 16. 実験結果（2） • log evidenceratio 𝐸 𝑤0 をプロットすると評価精度と相関
- 17.
- 18. SGDと汎化 • ベイズ証拠を最大化するためにベイズではノイズを加える [Mandt etal., 2017; Welling & Teh, 2011] • SGDでも同じことが起こっていると考えられる • バッチサイズを大きくするとノイズが減るので汎化性能が下がる
- 19. SGDのスケーリング則 • 更新式より、SGDによって発生するノイズの大きさは以下の式 に従う（導出は論文参照） 𝑔 ≈ 𝜖𝑁 𝐵 ただし𝜖：学習率、𝑁：学習セットサイズ、𝐵：バッチサイズ • Momentum SGDの場合は 𝑔 ≈ 𝜖𝑁 𝐵(1 − 𝑚) • したがって𝑔を変えないようにバッチサイズと学習率を調整す れば精度は維持される • 以上の関係が成り立っていることが実験より示される
- 20. 実験 • 隠れ層800次元の浅いネットワークでMNISTを学習 線形モデルには避けるべきsharp minimaが存在しないため •バッチサイズをさまざまに変化させ評価セットでのaccuracyを 比較する • optimizerはMomentum SGD 学習率: 1.0 momentum: 0.9
- 21. 実験結果（1） • full batchとminibatchの比較
- 22.
- 23.
- 24.
- 25. まとめ 1. Zhangの結果はDeep Learningに特有ではなく、より小さな 線形モデルでも観察できる。 この現象はベイズ証拠を評価することで説明できる。 2.SGDが汎化するのはノイズによる。このノイズの 大きさは𝑔 ≈ 𝜖𝑁 𝐵 に 従う。ノイズの大きさには最適値が存在し、 したがって最適なバッチサイズは学習率𝜖および学習データサ イズ𝑁に比例する。
- 26. 疑問・考察 • ベイズ証拠が大きいということは事前分布に対する学習データ セットの影響が小さいことを意味する。これは結局、学習が汎 化するか否かは、データセットとモデルの相性の問題でしかな いことを意味しているのではないか？ Deep ImagePrior(https://arxiv.org/abs/1711.10925)によればCNN自 体が強力な事前知識になっている • モデルとデータの相性が汎化性能のupper boundを規定し、 SGDはその中で性質の良い解を見つけることができる、という 構図？