Download as PDF, PPTX
![コードも載せとくね
x <- rnorm(100)
y <- rnorm(100)
data <- data.frame(type=1, x, y)
library(kernlab)
data.ksvm<- ksvm(type~.,data=data,type="one-svc",kernel="rbfdot",kpar=list
(sigma=0.1),nu=0.01,cross=10)
data.ksvm.predict <- predict(data.ksvm)
data.ksvm.predict <- ifelse(data.ksvm.predict==TRUE, 1, 2)
data.result <- cbind(data,data.ksvm.predict)
plot(data.result[,2:3], pch=21, bg=c("red","blue")[data.result$data.ksvm.predict])
１万はちょっと時間かかったから、前者の例です
2013年11月26日火曜日](https://image.slidesharecdn.com/8svm-131126053343-phpapp02/85/8-svm-30-320.jpg)
![[DL輪読会]深層強化学習はなぜ難しいのか？Why Deep RL fails? A brief survey of recent works.](https://cdn.slidesharecdn.com/ss_thumbnails/20210115dlohta-210115054939-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]ドメイン転移と不変表現に関するサーベイ](https://cdn.slidesharecdn.com/ss_thumbnails/20190614iwasawa-190614005939-thumbnail.jpg?width=640&height=640&fit=bounds)
![[Up用]rでqr](https://cdn.slidesharecdn.com/ss_thumbnails/uprqr-171202082902-thumbnail.jpg?width=640&height=640&fit=bounds)
はじパタ8章 svm
- 1.
- 2.
- 3.
- 4. ちょっとSVMの復習 SVMは下記のように、分類したい識別境界を求めるのでしたね。 ! 識 別境界：! Tx + b = 0 " !：識別境界の係数ベクトル（学習データから求める） " x：学習データ（d次元の特徴変数!データ数N→d!Nの 列） " b：バイアス項（学習データから求める） ! t = +1 t = -1 2013年11月26日火曜日 線形識別関数 ! Tx + b = 0
- 5. ちょっとSVMの復習 制約条件付きの凸計画問題を解く場合、ラグランジュの未定乗数法を用いる SVMの場合は制約条件が不等式となる 主問題 評価関数(最小化)：Lp(ω) = ½･ωTω←マージンの最小化 不等式制約条件：ti(ωTxi+b) ≧ 1 ←判別 ラグランジュ関数（これで制約付き凸計画を解く） N 1 T ~ L p (# , b, $ ) = # # " ! $ i (ti (# T xi + b )" 1) 2 i =1 αiはラグランジュ未定定数 α=(α1,･･･, αN) 2013年11月26日火曜日
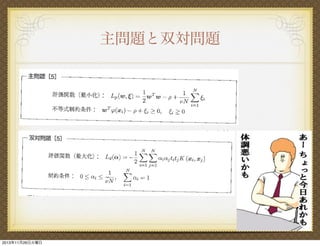
- 6. ちょっとSVMの復習 ! L d (!)を最 " Lp (#)を最 化する問題を「双対問題」と呼ぶ" 化する#を求めるほうが主問題! " 双対問題で対象とするラグランジュ関数 N 1 N N 評価関数 Ld (# ) = ! "" # i ti xi# j t j x j + " # i 2 i =1 j =1 i =1 (最 化) 1 T = # 1 ! # H# 2 #Tt = 0 T 制約条件 T H = ( H ij = ti t j xi x j ) t = (t1 , , , t N )T 2013年11月26日火曜日 #からじゃなく、 !から鞍点を探す
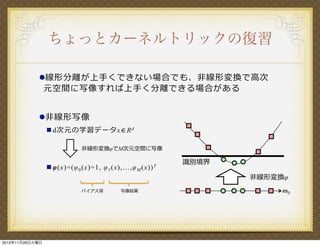
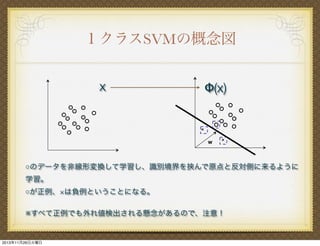
- 7. ちょっとカーネルトリックの復習 ! 線 形分離が上 くできない場合でも、線形変換で 元空間に写像すれば上 く分離できる場合がある 次 ! 線形写像 " d次元の学習データx∈R d 線形変換!でM次元空間に写像 " !(x)=(! 0 (x)=1, ! 1 (x),…,! M バイアス項 2013年11月26日火曜日 写像結果 (x)) T 識別境界 線形変換! !0
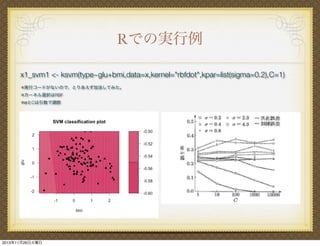
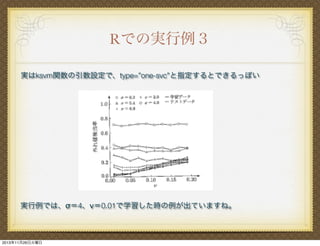
- 8. 動径基底カーネル（RBFカーネル） 多項式カーネルとは別にもう１つ内積で表すカーネルがあります。 σ：カーネル関数の広がりを制御するパラメータ N N T h (! (x )) = ! 0 " ( x ) = !! i ti" T ( xi ) ! ( x ) = !! i ti K ( xi , x ) i=1 i=1 ココ！ σが大きいとき：入力データxから遠く離れている広範囲のサポートベクトルが関与 σが小さいとき：入力データxの近傍のサポートベクトルのみが関与 2013年11月26日火曜日
- 9.
- 10.
- 11. Rでの実行例 library(MASS)内のPima.trでRBFカーネルの識別具合を実行する例が載っている。 WHOがインディアン女性の健康データを取得したものらしい。 > Pima.tr npreg glubp skin bmi ped age type 1 5 86 68 28 30.2 0.364 24 No 2 7 195 70 33 25.1 0.163 55 Yes 3 5 77 82 41 35.8 0.156 35 No 4 0 165 76 43 47.9 0.259 26 No 5 0 107 60 25 26.4 0.133 23 No 6 5 97 76 27 35.6 0.378 52 Yes 7 3 83 58 31 34.3 0.336 25 No 8 1 193 50 16 25.9 0.655 24 No 9 3 142 80 15 32.4 0.200 63 No 10 2 128 78 37 43.3 1.224 31 Yes 2013年11月26日火曜日 このtypeをglu、bmiを用いて kernlabパッケージのksvm関数を用いて、 RBFカーネルのσとCのパラメータを 調整して、その識別精度を検証。
- 12.
- 13. Νーサポートベクトルマシーン ソフトマージン識別機では、誤識別数の上限を抑えるためにCという定数パラメー タを使っていました。 N N N 1 T ~ L p($ , b, % , # , µ ) = $ $ + C ! # i " ! % i (ti ($ T xi + b )" 1 + # i )" ! µi# i 2 i =1 i =1 i =1 しかし、母集団からの標本が変わると誤識別数も変化してしまいます。 学習器の複雑さと達成可能な誤識別率には関連性があるので、 そのトレードオフをνというパラメータを介したものがν-SVMです。 ※タイトルのはどうしても小文字で表記できなかったので大文字表記です。 すみません。。 2013年11月26日火曜日
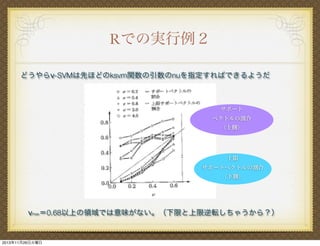
- 14. 何を変えたの？ CクラスSVMの場合の損失関数は ξi =f +(1-tif (xi)) ν-SVMの場合の損失関数は ξi =f +(ρ- tif (xi)) ρの値を最適化することを考えます。 学習機械は損失を小さくする方にはたらくので、損失関数としては マージンの大きさを決める値ρが小さければ小さいほど損失は小さくなる。 しかし、小さくなりすぎると汎化性能が下がる。 2013年11月26日火曜日
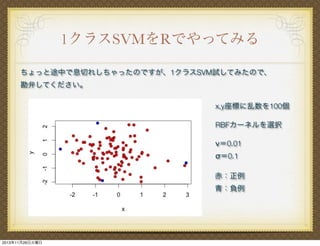
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30. コードも載せとくね x <- rnorm(100) y<- rnorm(100) data <- data.frame(type=1, x, y) library(kernlab) data.ksvm<- ksvm(type~.,data=data,type="one-svc",kernel="rbfdot",kpar=list (sigma=0.1),nu=0.01,cross=10) data.ksvm.predict <- predict(data.ksvm) data.ksvm.predict <- ifelse(data.ksvm.predict==TRUE, 1, 2) data.result <- cbind(data,data.ksvm.predict) plot(data.result[,2:3], pch=21, bg=c("red","blue")[data.result$data.ksvm.predict]) 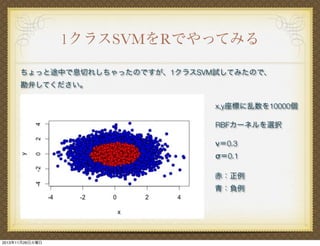１万はちょっと時間かかったから、前者の例です 2013年11月26日火曜日
- 31.
- 32.
- 33.