Документ представляет собой домашнюю работу по алгебре для 7 класса, основанную на учебнике 'Алгебра: учеб. для 7 кл. общеобразоват. учреждений'. В работе рассматриваются числовые и алгебраические выражения, а также упражнения на подтверждение равенств и решение задач. Также приводятся примеры и решения различных математических задач с подробными расчетами.










![11
4) ( )3232
2323 abmaabma −+−+=−+−
47. 1) 2a + 3b + m – c = 2a + 3b – (– m + c)
2) 2a + b + m – 3c = 2a + b – (– m + 3c)
3) ( )2222
3232 bamcbamc −+−=+−−
4) ( )3232
2323 abmaabma +−−=−+−
48. 1) (5a – 2b) – (3b – 5a) = 5a – 2b – 3b + 5a = 10a – 5b = 5(2a – b)
2) (6a – b) – (2a + 3b) = 6a – b – 2a – 3b = 4a – 4b = 4(a – b)
3) 7x + 3y – (– 3x + 3y) = 7x + 3y + 3x – 3y =10x
4) 8x – (3x – 2y) – 5y = 8x – 3x + 2y – 5y = 5x – 3y
49. 1) (2c + 5d) – (c + 4d) = 2c +5d – c – 4d = c + d
c = 0,4;
d = 0,6: 0,4 + 0,6 = 1
2) (2a – 4b) – (2a + 3d) = 3a – 4b – 2a + 3b = a – d
a = 0,12;
b = 1,28: 0,12 – 1,28 = – 1,16
3) (7x + 8y) – (5x – 2y) = 7x + 8y – 5x + 2y = 2x +10y
025,0;
4
3
=−= yx
25,125,05,1025,010
4
3
2 −=+−=⋅+⎟
⎠
⎞
⎜
⎝
⎛
−⋅
4) (5c – 6b) – (3c – 5b) = 5c – 6b – 3c + 5d = 2c – b
( ) 3
2
1
2
2
1
2
1
225,02:
2
1
2;25,0 −=−−=−−⋅=−= bc
50. 1) ( ) ( ) nmnmnmnmnmnm +=++=+=+−− 3:3;333458
( ) ( )[ ] 3:458 nmnm −−−⇒
2) ( ) ( ) nmnmnmnmmnnm +=++=+=−+− 4:4;444735
( ) ( )[ ] 4:735 mnnm −+−⇒
51. ( ) ( )( ) 012657106657532 <−=−+−−=−−−− aaaa при любых a.
52. 1) =++=+++++ cbaabccba 101201011010010100
= ( ) .20101 bca ++
2) ( ) ( ) −++=++−++ cbaabсcba 101001010010100
( )cacaabc −=−=−−− 99999910100
( ) ( )caca −=− 119:99 ;](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-11-320.jpg)






































![50
249. 1) 222
45 ababa =−−+ ;
2) 2 3 2 42 3 2 3 3
p q p q q− − + =
3) a b ab a ab b a ab b a b ab2 2 2 2 2 2 2 2
2 3 5 4 2 3 9 6− + + + − − + − = − − +
4) 2 3 4 3 4 2 3 8 52 2 2 2 2 2 2
a ab b a ab b a ab b b ab− + − − + + + + = −
250. 1) ( ) ( )7 9 2 8 1x x− + − = ; 2) ( ) ( ) 337512 =−++ xx
7 9 2 8 1x x− + − = ; 12 5 7 3 3x x+ + − =
9 18x = ; 99 −=x
x = 2 ; x = −1
3) ( ) ( )0 2 7 6 01 2, ,x x− − − = ; 4) ( ) ( )1 51 17 5 4 1− − + =, , ,x x
21,0672,0 =+−− xx ; 1 51 17 5 4 1− − − =, , ,x x
0 3 15, x = ; − =6 8 5 4, ,x
x = 50 ; x = −
27
34
251. 1) [ ] ( ) ,525105)4()3()2()1( M+⋅=+=++++++++ nnnnnnn
т.к. ( )5 2 5 2⋅ + = +n n: .
2) ( ) ( ) ( ) ( )[ ] ( )2 1 2 3 2 5 2 7 8 16 8 2 8n n n n n n+ + + + + + + = + = ⋅ + M ,
т.к. ( )8 2 8 2⋅ + = +n n: .
252. 1) ( )( )( )=−+−−−−+ 2222222
65,510585,12 yxxyxyx
( )12 5 8 5 10 55 62 2 2 2 2 2 2
, ,x y x y x x y+ − − + − + =
12 5 8 5 10 55 6 02 2 2 2 2 2 2
, ,x y x y x x y+ − + − + − =
2) ( )( )0 6 2 3 2 42 3 3 2 3 2 3
, ,ab a b ab a ab b+ + − − + −⎛
⎝
⎜ ⎞
⎠
⎟ =
( )0 6 2 3 2 42 3 3 2 3 2 3
, ,ab a b ab a ab b+ + − − − + =
0 6 2 3 2 4 32 3 3 2 3 2 3 3
, ,ab a b ab a ab b a+ + − + + − =
253. Пусть а – число десятков в этом числе; b – число единиц.
Так как десятков втрое больше, то а = 3b,
( )30 10 3 36b b b b+ − + = .
18 36b = ; b = 2
a = ⋅ =3 2 6
Ответ: это число 62.](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-50-320.jpg)





![56
273. (по рис. 8, 9 учебника)
1) ( ) ( )S a b c dABCD = + ⋅ +
adbdbcaсSSSSS LEBMLFCEKLPDAMLKABCD +++=+++= ч.т.д.
2) ( ) ( )S a b c dABFE = + ⋅ −
S S S S S ac ad bc bdABFE AMND BMNC DNKE CNRF= − + − = − + − ч.т.д.
274. ( ) ( ) ( ) ( )a b b a a b⋅ + + ⋅ + = + ⋅ +1 1 1 1 ;
2 1ab a b ab b a+ + = + + + ; 2 1ab a b ab b a+ + − − − = ; ab = 1 ч.т.д.
275. Пусть х м. – ширина прямоугольника; тогда (х + 15) м. – длина
прямоугольника, а его площадь S = ( )15+⋅ xx м3
;
(х + 8) м – ширина нового прямоугольника; [ (х +15) – 6 ] м –
длина нового прямоугольника, [ ]6)15()2( −++=′ xxS м2
– его
площадь
( ) ( ) ( )x x x x+ ⋅ + − ⋅ + =8 9 15 80 ; x x x x x2 2
8 9 72 15 80+ + + − − =
2 8x =
x = 4 (м.) – ширина прямоугольника
4 + 15 = 19 (м.) – длина прямоугольника
S = ⋅ =4 19 76 (м2
)
Ответ: 76 м2
276. Пусть х см. – ширина прямоугольника; тогда (30 – х) см. – дли-
на прямоугольника, а его площадь )30( хxS −= см2
;
(х – 6) см. – ширина нового прямоугольника; [(30 – х) + 10] см –
длина нового прямоугольника, а его площадь
)40()6( хxS −⋅−=′ см2
( ) ( ) ( )x x x x⋅ − − − ⋅ − =30 6 40 32 ; 3262404030 22
=−++− xxxx
20816 =x
x = 13 (см.) – ширина прямоугольника
30 – 13 = 17 (см.) – длина прямоугольника
S = ⋅ =13 17 221 (см2
)
Ответ: 221 см2
277. 1) ( ) ( ) ( ) ( ) ( ) +=++⋅+−−=++⋅⋅−⋅− 422
1221112 nnnnnnnnnn
12212222 234223233
++−−=+++−−−−+ nnnnnnnnnnn
( ) ( ) ( ) +−−−=−−⋅−−=−− 32342222
111 nnnnnnnnnn
1221 23422
++−−=++−++ nnnnnnnn ч.т.д.](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-56-320.jpg)














![71
347. 1) ( )x x x2
4 4 0− + − = ; 2) ( ) 028472
=−−+ xхx
( ) ( )x x x⋅ − + − =4 4 0 ; ( ) ( )x x x⋅ + − ⋅ + =7 4 7 0
( ) ( )x x− ⋅ + =4 1 0 ; ( ) ( )x x+ ⋅ − =7 4 0
x x+ = − =1 0 4 0; ; x x− = + =4 0 7 0;
;11 −=x ; ;41 =x
42 =x 72 −=x
3) ( )5 10 2 02
x x x− + − = ; 4) ( )3 12 4 02
x x x+ − + =
( ) ( )5 2 2 0x x x⋅ − + − = ; ( ) ( ) 0443 =+−+⋅ xxx
( ) ( )x x− ⋅ + =2 5 1 0 ; ( ) ( )x x+ ⋅ − =4 3 1 0
x x− = + =2 0 5 1 0; ; x x+ = − =4 0 3 1 0;
x x1 2
1
5
2= − =; ; x x1 24
1
3
= − =;
348. ( ) ( )[ ] ( )
( ) ( )[ ]x x x x x
x x x x
x
3 2 2
3 2 6 2
3 2 3
2
− − − − =
⋅ ⋅ − − ⋅ −
−
=:
( ) ( )
( )
x x x
x
x x x x
⋅ − ⋅ −
−
= ⋅ − = −
3 2
2
3 32
349. 1) ( )=+++=+++=++ 2)2(2223 222
xxxxxxxx
( ) ( ) ( ) ( )= ⋅ + + + = + ⋅ +x x x x x2 2 2 1
2) ( ) ( )=−⋅−−⋅=+−−=+− 23263265 22
xxxxxxxx
( ) ( )32 −⋅−= xx
3) ( ) ( ) ( ) ( )x x x x x x x x x x2 2
7 8 8 8 8 8 8 1− − = − + − = ⋅ − + − = − ⋅ +
4) ( )=+−+=−−+=−+ 10)10(1010109 222
xxxxxxxx
( ) ( ) ( ) ( )= ⋅ + − + = + ⋅ −x x x x x10 10 10 1
350. 1) =−+−=−−+=−+ )()33(3332 23222323
aaaaaaaa
)33)(1()1()1)(1(3)1()1(3 2222
aaaaaaaaaa ++−=−++−=−+−=
2) ( ) ( ) ( )x x x x x x x x x3 3
7 6 6 6 1 1 6 1− + = − − + = ⋅ − ⋅ + − ⋅ − =
( ) ( ) =−−+⋅−=−+⋅−= )623(1)6(1 22
xxxxxxx
( ) ( ) ( )[ ] ( ) ( ) ( )= − ⋅ ⋅ + − ⋅ + = − ⋅ + ⋅ −x x x x x x x1 3 2 3 1 3 2](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-71-320.jpg)


























































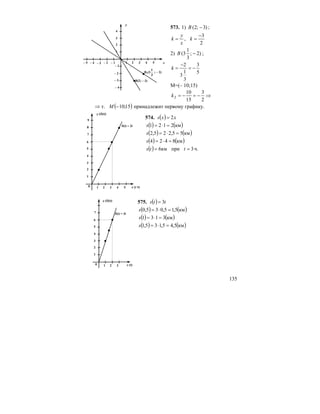

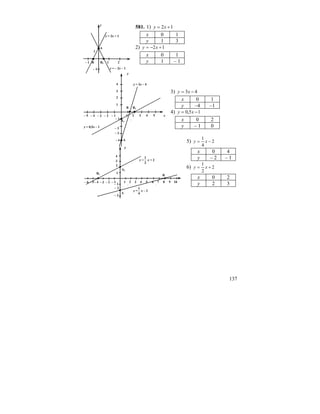

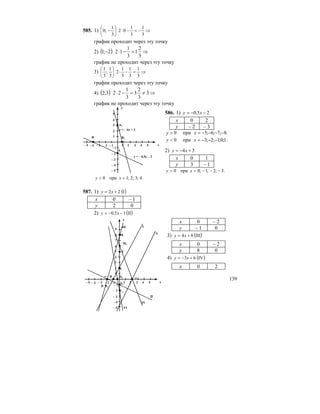
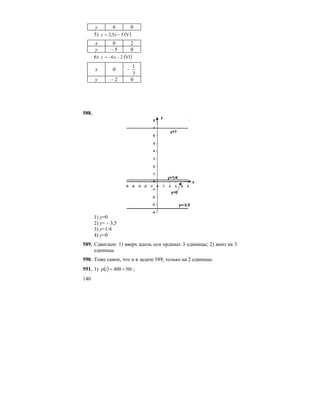
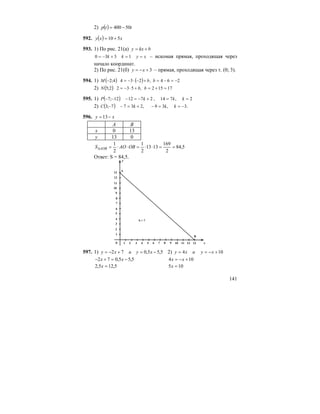
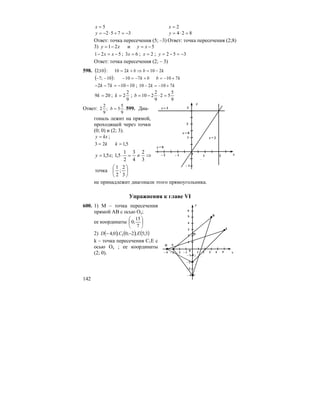


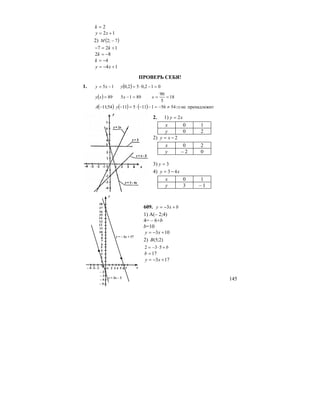
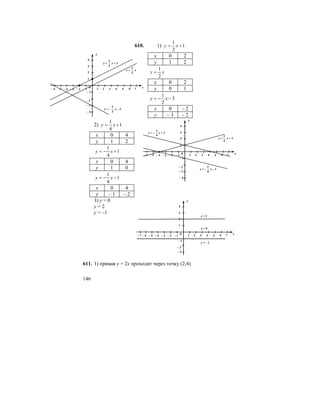































![MijZ`g_gby ^yihlhj_gbydmjkZZe]_[ju9,, deZkkZ](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-180-320.jpg)







![Hl_l
LZddZdqbkehkhklhblbaZ khl_gE ^_kyldhb k _^bgbplh kh
klZbfnhjfmemZ E F
?kebqbkehaZibkZgh h[jZlghfihjy^d_lhnhjfmeZlZdZy
k E D
LZddZdd] ]lhZ dbeh]jZffhb k ]jZffhkh^_j`Zl
Z k](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-191-320.jpg)
![]jZffh](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-192-320.jpg)


















![[[
± o o o ± o ±
o o
o
[
Hl_l Hl_l
Imklv i_jhcdhjh[d_o dZjZg^Zr_cLh]^Zhlhjhc± o ±](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-212-320.jpg)

![k_]h[uehdZjZg^Zr_cihwlhfm
o o ±](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-214-320.jpg)

![o
o ± i_jhcdhjh[d_
o ± ± hlhjhcdhjh[d_
o ± lj_lv_cdhjh[d_
Hl_l
Imklvq_j_ao e_lhl_p[m^_lljh_klZjr_kugZLh]^Z
o ˜ o](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-216-320.jpg)

![Imklvo dfq ± kdhjhklvdZl_jZLh]^Zo](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-218-320.jpg)



![o o ±
o dfq ± kdhjhklvdZl_jZ
dfq ± kdhjhklvihl_q_gbxj_db
6 ˜ df
Hl_ldf
Imklvo dfq ± kdhjhklv_jlhe_lZLh]^Zo](https://image.slidesharecdn.com/720021-801-130411121550-phpapp02/85/7-_2002-1-801-222-320.jpg)