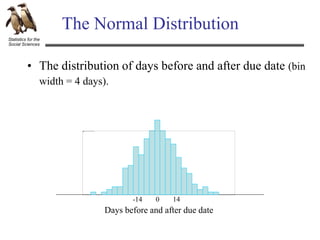
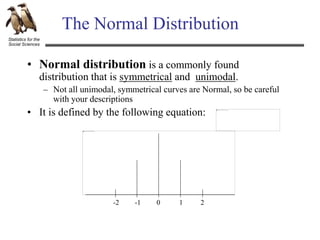
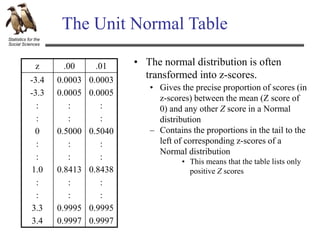
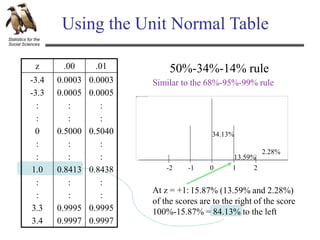
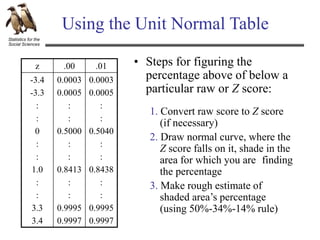
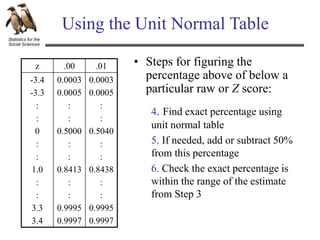
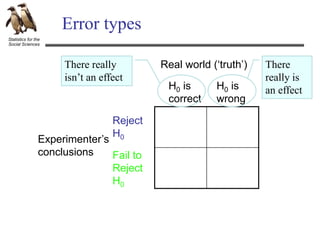
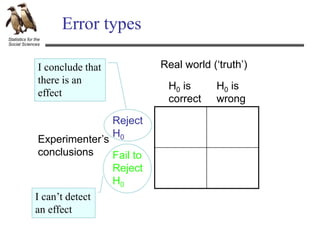
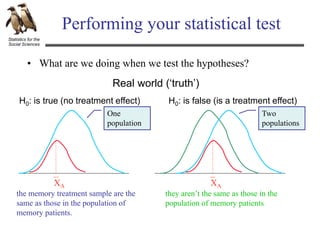
The document discusses hypothesis testing using an example of testing the effectiveness of a new memory treatment. It outlines the five steps of hypothesis testing: 1) stating the null and alternative hypotheses, 2) setting the decision criteria, 3) collecting the data, 4) computing test statistics, and 5) making a decision about the null hypothesis. Specifically, it provides details about testing the effectiveness of a new drug treatment for patients with memory problems by comparing memory test errors between those who received the treatment and those who did not. It states that the goal is to determine if the difference observed is a real effect of the treatment or just sampling error.

1. Statistics for the Social Sciences
Psychology 340
Fall 2006
Hypothesis testing

2. Statistics for the
Social Sciences
Outline (for week)
• Review of:
– Basic probability
– Normal distribution
– Hypothesis testing framework
• Stating hypotheses
• General test statistic and test statistic distributions
• When to reject or fail to reject

3. Statistics for the
Social Sciences
Hypothesis testing
• Example: Testing the effectiveness of a new memory
treatment for patients with memory problems
– Our pharmaceutical company develops a new drug
treatment that is designed to help patients with impaired
memories.
– Before we market the drug we want to see if it works.
– The drug is designed to work on all memory patients, but
we can’t test them all (the population).
– So we decide to use a sample and conduct the following
experiment.
– Based on the results from the sample we will make
conclusions about the population.

4. Statistics for the
Social Sciences
Hypothesis testing
• Example: Testing the effectiveness of a new memory
treatment for patients with memory problems
Memory
treatment
No Memory
treatment
Memory
patients
Memory
Test
Memory
Test
55
errors
60
errors
5 error
diff
• Is the 5 error difference:
– A “real” difference due to the effect of the treatment
– Or is it just sampling error?

5. Statistics for the
Social Sciences
Testing Hypotheses
• Hypothesis testing
– Procedure for deciding whether the outcome of a study
(results for a sample) support a particular theory (which
is thought to apply to a population)
– Core logic of hypothesis testing
• Considers the probability that the result of a study could have
come about if the experimental procedure had no effect
• If this probability is low, scenario of no effect is rejected and
the theory behind the experimental procedure is supported

6. Statistics for the
Social Sciences
Basics of Probability
• Probability
– Expected relative frequency of a particular outcome
• Outcome
– The result of an experiment

7. Statistics for the
Social Sciences
Flipping a coin example
What are the odds of getting a “heads”?
One outcome classified as heads
=
1
2
= 0.5
Total of two outcomes
n = 1 flip

8. Statistics for the
Social Sciences
Flipping a coin example
What are the odds of
getting two “heads”?
Number of heads
2
1
1
0
One 2 “heads”
outcome
Four total
outcomes
= 0.25
This situation is known as the binomial # of outcomes = 2n
n = 2

9. Statistics for the
Social Sciences
Flipping a coin example
What are the odds of
getting “at least one
heads”?
Number of heads
2
1
1
0
Four total
outcomes
= 0.75
Three “at least one
heads” outcome
n = 2

10. Statistics for the
Social Sciences
Flipping a coin example
HHH
HHT
HTH
HTT
THH
THT
TTH
TTT
Number of heads
3
2
1
0
2
2
1
1
2n = 23 = 8 total outcomes
n = 3

11. Statistics for the
Social Sciences
Flipping a coin example
Number of heads
3
2
1
0
2
2
1
1
X f p
3 1 .125
2 3 .375
1 3 .375
0 1 .125
Number of heads
0 1 2 3
.1
.2
.3
.4
probability
.125 .125
.375
.375
Distribution of possible outcomes
(n = 3 flips)

12. Statistics for the
Social Sciences
Flipping a coin example
Number of heads
0 1 2 3
.1
.2
.3
.4
probability
What’s the probability of
flipping three heads in a
row?
.125 .125
.375
.375 p = 0.125
Distribution of possible outcomes
(n = 3 flips)
Can make predictions about
likelihood of outcomes based on
this distribution.

13. Statistics for the
Social Sciences
Flipping a coin example
Number of heads
0 1 2 3
.1
.2
.3
.4
probability
What’s the probability of
flipping at least two heads
in three tosses?
.125 .125
.375
.375 p = 0.375 + 0.125 = 0.50
Can make predictions about
likelihood of outcomes based on
this distribution.
Distribution of possible outcomes
(n = 3 flips)

14. Statistics for the
Social Sciences
Flipping a coin example
Number of heads
0 1 2 3
.1
.2
.3
.4
probability
What’s the probability of
flipping all heads or all tails
in three tosses?
.125 .125
.375
.375 p = 0.125 + 0.125 = 0.25
Can make predictions about
likelihood of outcomes based on
this distribution.
Distribution of possible outcomes
(n = 3 flips)

15. Statistics for the
Social Sciences
Hypothesis testing
Can make predictions about
likelihood of outcomes based on
this distribution.
Distribution of possible outcomes
(of a particular sample size, n)
• In hypothesis testing, we
compare our observed samples
with the distribution of possible
samples (transformed into
standardized distributions)
• This distribution of possible
outcomes is often Normally
Distributed

16. Statistics for the
Social Sciences
The Normal Distribution
• The distribution of days before and after due date (bin
width = 4 days).
0 14
-14
Days before and after due date

17. Statistics for the
Social Sciences
The Normal Distribution
• Normal distribution

18. Statistics for the
Social Sciences
The Normal Distribution
• Normal distribution is a commonly found
distribution that is symmetrical and unimodal.
– Not all unimodal, symmetrical curves are Normal, so be careful
with your descriptions
• It is defined by the following equation:
1 2
-1
-2 0

19. Statistics for the
Social Sciences
The Unit Normal Table
z .00 .01
-3.4
-3.3
:
:
0
:
:
1.0
:
:
3.3
3.4
0.0003
0.0005
:
:
0.5000
:
:
0.8413
:
:
0.9995
0.9997
0.0003
0.0005
:
:
0.5040
:
:
0.8438
:
:
0.9995
0.9997
• Gives the precise proportion of scores (in
z-scores) between the mean (Z score of
0) and any other Z score in a Normal
distribution
– Contains the proportions in the tail to the
left of corresponding z-scores of a
Normal distribution
• This means that the table lists only
positive Z scores
• The normal distribution is often
transformed into z-scores.

20. Statistics for the
Social Sciences
Using the Unit Normal Table
z .00 .01
-3.4
-3.3
:
:
0
:
:
1.0
:
:
3.3
3.4
0.0003
0.0005
:
:
0.5000
:
:
0.8413
:
:
0.9995
0.9997
0.0003
0.0005
:
:
0.5040
:
:
0.8438
:
:
0.9995
0.9997
15.87% (13.59% and 2.28%)
of the scores are to the right of the score
100%-15.87% = 84.13% to the left
At z = +1:
13.59%
2.28%
34.13%
50%-34%-14% rule
1 2
-1
-2 0
Similar to the 68%-95%-99% rule

21. Statistics for the
Social Sciences
Using the Unit Normal Table
z .00 .01
-3.4
-3.3
:
:
0
:
:
1.0
:
:
3.3
3.4
0.0003
0.0005
:
:
0.5000
:
:
0.8413
:
:
0.9995
0.9997
0.0003
0.0005
:
:
0.5040
:
:
0.8438
:
:
0.9995
0.9997
1. Convert raw score to Z score
(if necessary)
2. Draw normal curve, where the
Z score falls on it, shade in the
area for which you are finding
the percentage
3. Make rough estimate of
shaded area’s percentage
(using 50%-34%-14% rule)
• Steps for figuring the
percentage above of below a
particular raw or Z score:

22. Statistics for the
Social Sciences
Using the Unit Normal Table
z .00 .01
-3.4
-3.3
:
:
0
:
:
1.0
:
:
3.3
3.4
0.0003
0.0005
:
:
0.5000
:
:
0.8413
:
:
0.9995
0.9997
0.0003
0.0005
:
:
0.5040
:
:
0.8438
:
:
0.9995
0.9997
4. Find exact percentage using
unit normal table
5. If needed, add or subtract 50%
from this percentage
6. Check the exact percentage is
within the range of the estimate
from Step 3
• Steps for figuring the
percentage above of below a
particular raw or Z score:

23. Statistics for the
Social Sciences
Suppose that you got a 630 on the SAT. What percent of
the people who take the SAT get your score or worse?
SAT Example problems
• The population parameters for the SAT are:
m = 500, s = 100, and it is Normally distributed
From the table:
z(1.3) =.0968
That’s 9.68%
above this score
So 90.32% got your
score or worse

24. Statistics for the
Social Sciences
The Normal Distribution
• You can go in the other direction too
– Steps for figuring Z scores and raw scores from
percentages:
1. Draw normal curve, shade in approximate area for the
percentage (using the 50%-34%-14% rule)
2. Make rough estimate of the Z score where the shaded area
starts
3. Find the exact Z score using the unit normal table
4. Check that your Z score is similar to the rough estimate from
Step 2
5. If you want to find a raw score, change it from the Z score

25. Statistics for the
Social Sciences
Inferential statistics
• Hypothesis testing
– Core logic of hypothesis testing
• Considers the probability that the result of a study could have
come about if the experimental procedure had no effect
• If this probability is low, scenario of no effect is rejected and
the theory behind the experimental procedure is supported
• Step 1: State your hypotheses
• Step 2: Set your decision criteria
• Step 3: Collect your data
• Step 4: Compute your test statistics
• Step 5: Make a decision about your null hypothesis
– A five step program

26. Statistics for the
Social Sciences
– Step 1: State your hypotheses: as a research hypothesis and a
null hypothesis about the populations
• Null hypothesis (H0)
• Research hypothesis (HA)
Hypothesis testing
• There are no differences between conditions (no effect of treatment)
• Generally, not all groups are equal
This is the one that you test
• Hypothesis testing: a five step program
– You aren’t out to prove the alternative hypothesis
• If you reject the null hypothesis, then you’re left with
support for the alternative(s) (NOT proof!)

27. Statistics for the
Social Sciences
In our memory example experiment:
Testing Hypotheses
mTreatment > mNo Treatment
mTreatment < mNo Treatment
H0:
HA:
– Our theory is that the
treatment should improve
memory (fewer errors).
– Step 1: State your hypotheses
• Hypothesis testing: a five step program
One -tailed

28. Statistics for the
Social Sciences
In our memory example experiment:
Testing Hypotheses
mTreatment > mNo Treatment
mTreatment < mNo Treatment
H0:
HA:
– Our theory is that the
treatment should improve
memory (fewer errors).
– Step 1: State your hypotheses
• Hypothesis testing: a five step program
mTreatment = mNo Treatment
mTreatment ≠ mNo Treatment
H0:
HA:
– Our theory is that the
treatment has an effect on
memory.
One -tailed Two -tailed
no direction
specified
direction
specified

29. Statistics for the
Social Sciences
One-Tailed and Two-Tailed Hypothesis Tests
• Directional
hypotheses
– One-tailed test
• Nondirectional
hypotheses
– Two-tailed test

30. Statistics for the
Social Sciences
Testing Hypotheses
– Step 1: State your hypotheses
– Step 2: Set your decision criteria
• Hypothesis testing: a five step program
• Your alpha () level will be your guide for when to reject or fail
to reject the null hypothesis.
– Based on the probability of making making an certain type of error

31. Statistics for the
Social Sciences
Testing Hypotheses
– Step 1: State your hypotheses
– Step 2: Set your decision criteria
– Step 3: Collect your data
• Hypothesis testing: a five step program

32. Statistics for the
Social Sciences
Testing Hypotheses
– Step 1: State your hypotheses
– Step 2: Set your decision criteria
– Step 3: Collect your data
– Step 4: Compute your test statistics
• Hypothesis testing: a five step program
• Descriptive statistics (means, standard deviations, etc.)
• Inferential statistics (z-test, t-tests, ANOVAs, etc.)

33. Statistics for the
Social Sciences
Testing Hypotheses
– Step 1: State your hypotheses
– Step 2: Set your decision criteria
– Step 3: Collect your data
– Step 4: Compute your test statistics
– Step 5: Make a decision about your null hypothesis
• Hypothesis testing: a five step program
• Based on the outcomes of the statistical tests researchers will either:
– Reject the null hypothesis
– Fail to reject the null hypothesis
• This could be correct conclusion or the incorrect conclusion

34. Statistics for the
Social Sciences
Error types
• Type I error (): concluding that there is a
difference between groups (“an effect”) when
there really isn’t.
– Sometimes called “significance level” or “alpha level”
– We try to minimize this (keep it low)
• Type II error (): concluding that there isn’t an
effect, when there really is.
– Related to the Statistical Power of a test (1-)

35. Statistics for the
Social Sciences
Error types
Real world (‘truth’)
H0 is
correct
H0 is
wrong
Experimenter’s
conclusions
Reject
H0
Fail to
Reject
H0
There really
isn’t an effect
There
really is
an effect

36. Statistics for the
Social Sciences
Error types
Real world (‘truth’)
H0 is
correct
H0 is
wrong
Experimenter’s
conclusions
Reject
H0
Fail to
Reject
H0
I conclude that
there is an
effect
I can’t detect
an effect

37. Statistics for the
Social Sciences
Error types
Real world (‘truth’)
H0 is
correct
H0 is
wrong
Experimenter’s
conclusions
Reject
H0
Fail to
Reject
H0
Type I
error
Type II
error

38. Statistics for the
Social Sciences
Performing your statistical test
H0: is true (no treatment effect) H0: is false (is a treatment effect)
Two
populations
One
population
• What are we doing when we test the hypotheses?
Real world (‘truth’)
XA
they aren’t the same as those in the
population of memory patients
XA
the memory treatment sample are the
same as those in the population of
memory patients.

39. Statistics for the
Social Sciences
Performing your statistical test
• What are we doing when we test the hypotheses?
– Computing a test statistic: Generic test
Could be difference between a sample and a
population, or between different samples
Based on standard error or an
estimate of the standard error

40. Statistics for the
Social Sciences
“Generic” statistical test
• The generic test statistic distribution (think of this as the distribution
of sample means)
– To reject the H0, you want a computed test statistics that is large
– What’s large enough?
• The alpha level gives us the decision criterion
Distribution of the test statistic
-level determines where
these boundaries go

41. Statistics for the
Social Sciences
“Generic” statistical test
If test statistic is
here Reject H0
If test statistic is here
Fail to reject H0
Distribution of the test statistic
• The generic test statistic distribution (think of this as the distribution
of sample means)
– To reject the H0, you want a computed test statistics that is large
– What’s large enough?
• The alpha level gives us the decision criterion

42. Statistics for the
Social Sciences
“Generic” statistical test
Reject H0
Fail to reject H0
• The alpha level gives us the decision criterion
One -tailed
Two -tailed
Reject H0
Fail to reject H0
Reject H0
Fail to reject H0
 = 0.05
0.025
0.025
split up
into the
two tails

43. Statistics for the
Social Sciences
“Generic” statistical test
Reject H0
Fail to reject H0
• The alpha level gives us the decision criterion
One -tailed
Two -tailed
Reject H0
Fail to reject H0
Reject H0
Fail to reject H0
 = 0.05
0.05
all of it in
one tail

44. Statistics for the
Social Sciences
“Generic” statistical test
Reject H0
Fail to reject H0
• The alpha level gives us the decision criterion
One -tailed
Two -tailed
Reject H0
Fail to reject H0
Reject H0
Fail to reject H0
 = 0.05
0.05
all of it in
one tail

45. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
• Step 1: State your hypotheses
H0: the memory treatment
sample are the same as
those in the population of
memory patients.
HA: they aren’t the same as
those in the population of
memory patients
mTreatment > mpop > 60
mTreatment < mpop < 60

46. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
• Step 2: Set your decision
criteria
 = 0.05
One -tailed
H0: mTreatment > mpop > 60
HA: mTreatment < mpop < 60

47. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
 = 0.05
One -tailed
• Step 3: Collect your data
H0: mTreatment > mpop > 60
HA: mTreatment < mpop < 60

48. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
 = 0.05
One -tailed
• Step 4: Compute your test
statistics
= -2.5
H0: mTreatment > mpop > 60
HA: mTreatment < mpop < 60

49. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
 = 0.05
One -tailed
• Step 5: Make a decision
about your null hypothesis
5%
Reject H0
H0: mTreatment > mpop > 60
HA: mTreatment < mpop < 60

50. Statistics for the
Social Sciences
“Generic” statistical test
An example: One sample z-test
Memory example experiment:
• We give a n = 16 memory patients a
memory improvement treatment.
• How do they compare to the general
population of memory patients who have
a distribution of memory errors that is
Normal, m = 60, s = 8?
• After the treatment they have an
average score of = 55 memory errors.
 = 0.05
One -tailed
• Step 5: Make a decision
about your null hypothesis
- Reject H0
- Support for our HA, the
evidence suggests that the
treatment decreases the
number of memory errors
H0: mTreatment > mpop > 60
HA: mTreatment < mpop < 60