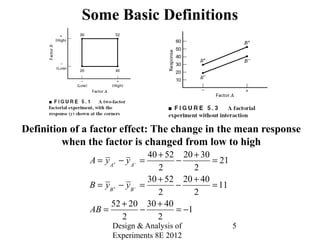
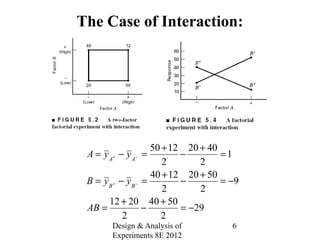
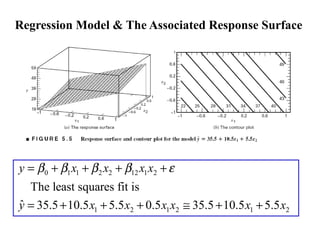
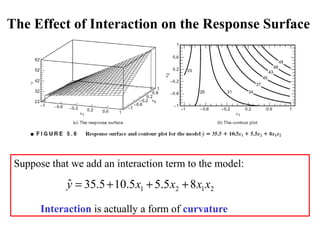
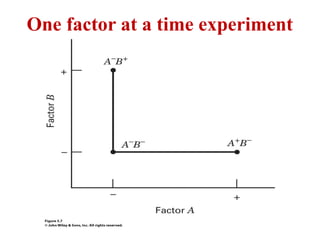
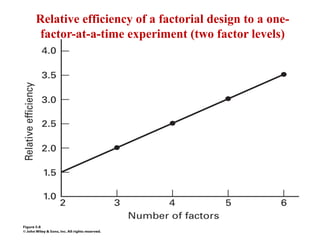
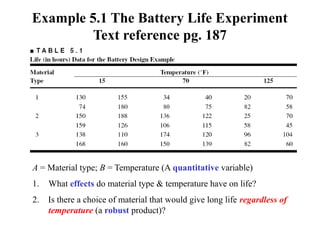
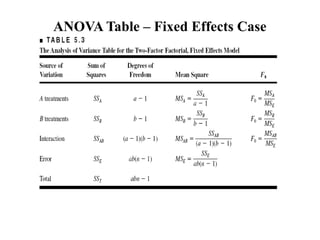
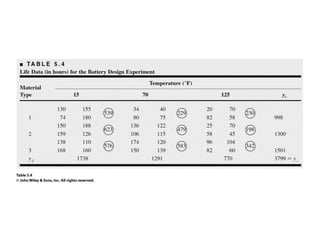
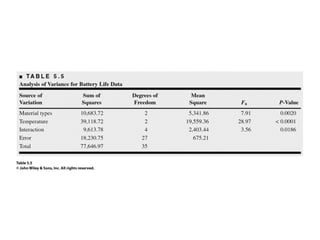
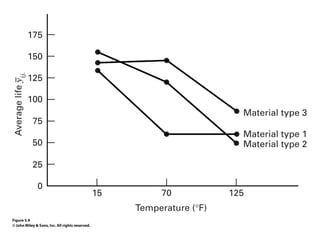
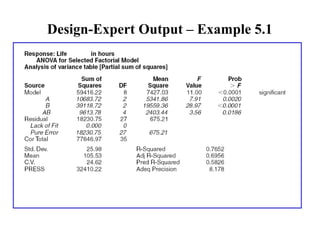
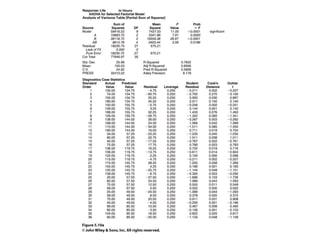
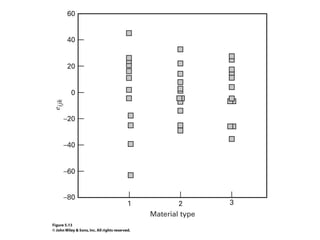
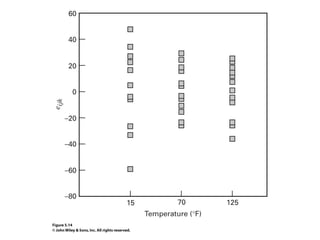
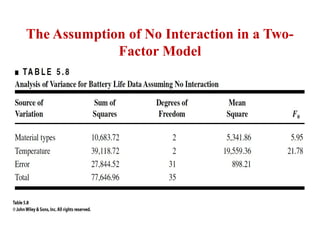
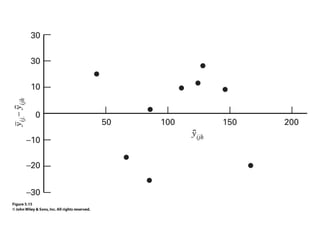
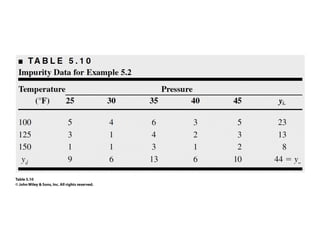
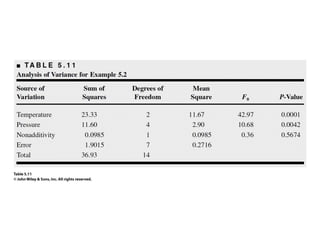
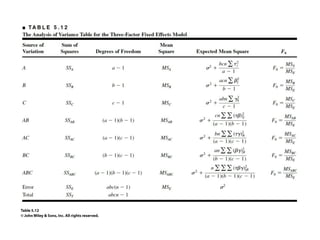
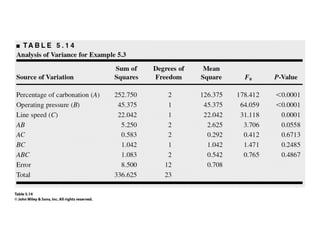
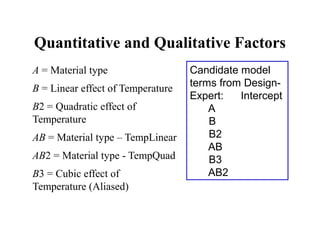
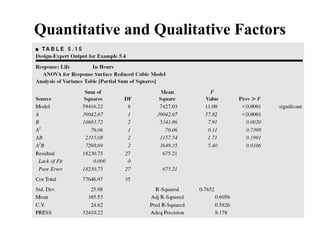
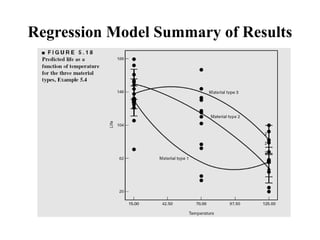
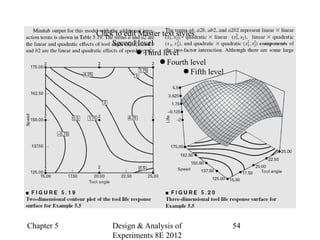
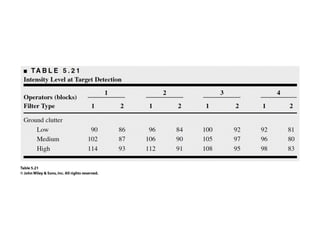
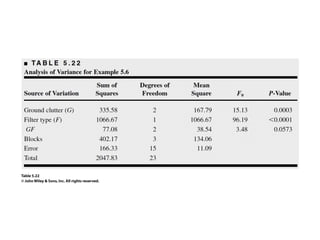
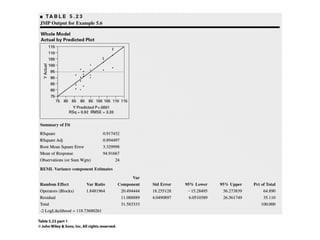
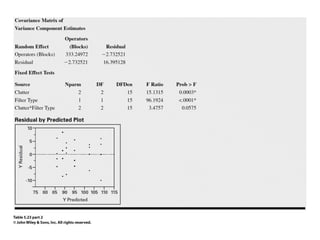
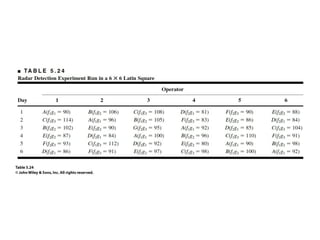
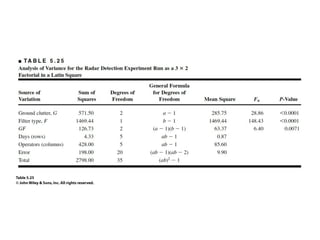
Factorial experiments allow researchers to study the effects of two or more factors simultaneously in a single experiment. This is more efficient than studying each factor individually. A two-factor factorial design involves all combinations of levels of two factors. The analysis of variance for factorial designs partitions the total variation into separate pieces for the main effects of each factor and their interaction. Factorial designs are extended to more than two factors in a similar manner. Factors can include both qualitative and quantitative variables. Response curves and surfaces are used to model and interpret the results involving quantitative factors.

1. Factorial Experiments
Dr. Jitesh J. Thakkar
INDIAN INSTITUTE OF TECHNOLOGY (IIT)
KHARAGPUR
KHARAGPUR – 721 302

2. Contents
• General principles of factorial experiments
• The two-factor factorial with fixed effects
• The ANOVA for factorials
• Extensions to more than two factors
• Quantitative and qualitative factors – response
curves and surfaces

3. Source
D. C. Montgomery, Design and analysis of
experiments, 7th edition

4. Basic Definition
• Many experiments involve the study of the effects
of two or more factors.
• Factorial designs most efficient for this type of
experiment.
• By a factorial design, we mean that in each
complete trial or replicate of the experiment all
possible combinations of the levels of the factors are
investigated
• If there are a levels of factor A and b levels of factor
B, each replicate contains all ab treatment
combinations.

5. Design & Analysis of
Experiments 8E 2012
5
Some Basic Definitions
Definition of a factor effect: The change in the mean response
when the factor is changed from low to high
40 52 20 30
21
2 2
30 52 20 40
11
2 2
52 20 30 40
1
2 2
A A
B B
A y y
B y y
AB
+ −
+ −
+ +
= − = − =
+ +
= − = − =
+ +
= − = −

6. Design & Analysis of
Experiments 8E 2012
6
The Case of Interaction:
50 12 20 40
1
2 2
40 12 20 50
9
2 2
12 20 40 50
29
2 2
A A
B B
A y y
B y y
AB
+ −
+ −
+ +
= − = − =
+ +
= − = − = −
+ +
= − = −

7. Regression Model & The Associated Response Surface
0 1 1 2 2 12 1 2
1 2 1 2 1 2
The least squares fit is
ˆ 35.5 10.5 5.5 0.5 35.5 10.5 5.5
y x x x x
y x x x x x x
β β β β ε= + + + +
= + + + ≅ + +

8. The Effect of Interaction on the Response Surface
Suppose that we add an interaction term to the model:
1 2 1 2
ˆ 35.5 10.5 5.5 8y x x x x= + + +
Interaction is actually a form of curvature

9. Select Insights
• When an interaction is large, the corresponding main effects have little
practical meaning.
• For the experiment in Figure 5.2, we would estimate the main effect of
A to be
• A=(50+12)/2 – (20+40)/2 = 1
• This is very small and we are tempted to conclude that there is no
effect due to A.
• When we examine the effects of A at different levels of factor B, we
see that this is not the case
• Factor A has an effect, but it depends on the level of factor B.
• Knowledge of AB interaction is more useful than knowledge of the
main effect.
• A significant interaction will often mask the significance of main
effects.

10. One factor at a time experiment

11. Insight
• If a factorial experiment had been performed, an additional treatment
combination, A+ B+ would have been taken
• Two estimates of the effect A can be made A+B- - A-B- and A+B+- A-
B+
• Two estimates of the B can be made similarly
• Two estimates of each main effect could be averaged to produce
average main effects that are just as precise as those from the single-
factor experiment, but only four total observations are required
• Relative efficiency of the factorial design to the one-factor-at-a-time
experiment is 6/4=1.5
• Relative efficiency will increase as the number of factors increases
• Factorial designs are necessary when interactions may be present to
avoid misleading conclusions.

12. Relative efficiency of a factorial design to a one-
factor-at-a-time experiment (two factor levels)

13. Example 5.1 The Battery Life Experiment
Text reference pg. 187
A = Material type; B = Temperature (A quantitative variable)
1. What effects do material type & temperature have on life?
2. Is there a choice of material that would give long life regardless of
temperature (a robust product)?

14. The General Two-Factor
Factorial Experiment
a levels of factor A; b levels of factor B; n replicates
This is a completely randomized design

15. Statistical (effects) model:
1,2,...,
( ) 1,2,...,
1,2,...,
ijk i j ij ijk
i a
y j b
k n
µ τ β τβ ε
=

= + + + + =
 =
Other models (means model, regression models) can be useful

16. Extension of the ANOVA to Factorials
(Fixed Effects Case) – pg. 189
2 2 2
... .. ... . . ...
1 1 1 1 1
2 2
. .. . . ... .
1 1 1 1 1
( ) ( ) ( )
( ) ( )
a b n a b
ijk i j
i j k i j
a b a b n
ij i j ijk ij
i j i j k
y y bn y y an y y
n y y y y y y
= = = = =
= = = = =
− = − + −
+ − − + + −
∑∑∑ ∑ ∑
∑∑ ∑∑∑
breakdown:
1 1 1 ( 1)( 1) ( 1)
T A B AB ESS SS SS SS SS
df
abn a b a b ab n
= + + +
− = − + − + − − + −

17. ANOVA Table – Fixed Effects Case

18. Design & Analysis of
Experiments 8E 2012
18
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

22. Multiple Comparison
• When ANOVA indicates that row or column means are
differ, it is usually of interest to make comparisons
between the individual row or column means to discover
specific differences
• Turkey’s test
• When interaction is significant, comparisons between the
means of one factor (e.g. A) may be obscured by the AB
interaction
• Fix factor B at a specific level and apply Turkey’s test toe
means of factor A at that level

23. Design-Expert Output – Example 5.1

25. Chapter 5 Design & Analysis of
Experiments 8E 2012
25
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth levelJMP output – Example 5.1

27. RESIDUALANALYSIS

32. Choice of Sample Size

33. The Assumption of No Interaction in a Two-
Factor Model

35. One Observation Per Cell

39. The General Factorial Design

40. Factorials with More Than
Two Factors
• Basic procedure is similar to the two-factor case; all
abc…kn treatment combinations are run in random
order
• ANOVA identity is also similar:
• Complete three-factor example in text, Example 5.5
T A B AB AC
ABC AB K E
SS SS SS SS SS
SS SS SS
= + + + + +
+ + + +L
L L
L

45. Fitting Response Curves and Surfaces
• The basic ANOVA procedure treats every factor as if it
were qualitative
• Sometimes an experiment will involve both quantitative
and qualitative factors, such as in Example 5.1
• This can be accounted for in the analysis to produce
regression models for the quantitative factors at each level
(or combination of levels) of the qualitative factors
• These response curves and/or response surfaces are often
a considerable aid in practical interpretation of the results

46. Quantitative and Qualitative Factors
Candidate model
terms from Design-
Expert: Intercept
A
B
B2
AB
B3
AB2
A = Material type
B = Linear effect of Temperature
B2 = Quadratic effect of
Temperature
AB = Material type – TempLinear
AB2 = Material type - TempQuad
B3 = Cubic effect of
Temperature (Aliased)

47. Quantitative and Qualitative Factors

48. Insights
• The P-value indicate that A2 and AB are not significant
whereas the A2B term is significant
• Often we think about removing non-significant terms or
factors from a model, but in this case, removing A2 and AB
and retaining A2B will result in a model that is not
hierarchical
• The hierarchical principle indicates that if a model contains a
high-order term (such as A2B), it should also contain all of
the lower order terms that compose it (in this case A2 and AB)
• Hierarchy promotes a type of consistency in the model

49. Regression Model Summary of Results

50. Chapter 5 Design & Analysis of
Experiments 8E 2012
50
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

51. Chapter 5 Design & Analysis of
Experiments 8E 2012
51
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

52. Chapter 5 Design & Analysis of
Experiments 8E 2012
52
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

53. Chapter 5 Design & Analysis of
Experiments 8E 2012
53
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

54. Chapter 5 Design & Analysis of
Experiments 8E 2012
54
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

55. Chapter 5 Design & Analysis of
Experiments 8E 2012
55
Click to edit Master text styles
Second level
● Third level
● Fourth level
● Fifth level

56. Blocking in a Factorial Design