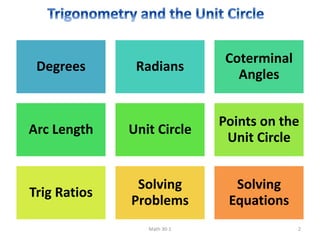
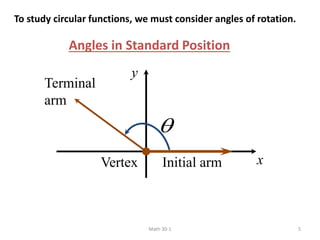
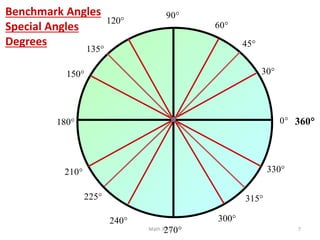
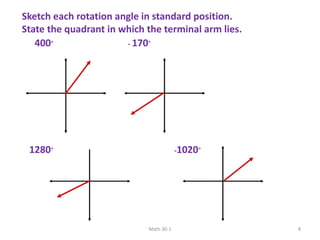
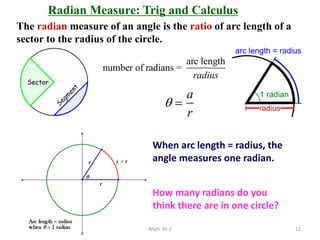
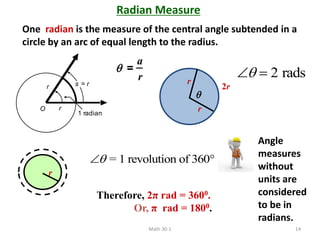
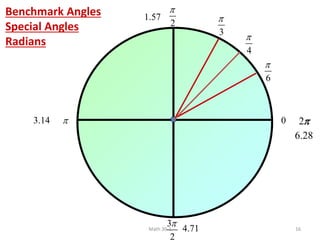
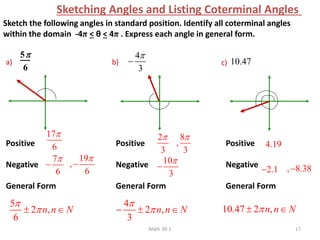
The document discusses trigonometry and circular functions. It defines trigonometry as the study of repeating, cyclical patterns through the use of trigonometric functions. It then provides information about measuring angles in degrees and radians, defining standard angle position, discussing coterminal angles, and converting between degree and radian measure.

1. Botanical Name
Narcissus 'Trigonometry'
Plant Common Name
Trigonometry Daffodil
The flowers of a Trigonometry Daffodil are of almost geometric
precision with their repeating patterns.
Repeating patterns occur in sound, light, tides, time, and nature.
To analyse these repeating, cyclical patterns, we need to study the
cyclical functions branch of trigonometry.
Math 30-1 1

2. Degrees Radians
Coterminal
Angles
Arc Length Unit Circle
Points on the
Unit Circle
Trig Ratios
Solving
Problems
Solving
Equations
Math 30-1 2

3. Angles
Degrees
Standard
Position
Angle Conversion
Radians
Coterminal
Angles
Arc Length
Math 30-1 3

4. Circular Functions
Angles can be measured in:
Degrees: common unit used in Geometry
1
part of a circle
360
Radian: common unit used in Trigonometry
1
part of a circle
2
Gradient: not common unit, used in surveying
1
part of a circle
400
Revolutions: angular velocity radians per second
Math 30-1 4

5. Angles in Standard Position

Initial arm
Vertex
Terminal
arm
x
y
To study circular functions, we must consider angles of rotation.
Math 30-1 5

6. If the terminal arm
moves counter-
clockwise, angle A
is positive.
A x
y
If the terminal side
moves clockwise,
angle A is
negative.
A
x
y
Positive or Negative Rotation Angle
McGraw Hill DVD Teacher Resources 4.1_178_IA
Math 30-1 6

7. 30
60
120
150
210
240 300
330
90
180
270
0
Benchmark Angles
Special Angles
Degrees 45
135
225 315
360
Math 30-1 7

8. Sketch each rotation angle in standard position.
State the quadrant in which the terminal arm lies.
400° - 170°
-1020°
1280°
Math 30-1 8

9. Coterminal angles are angles in standard position that share the
same terminal arm. They also share the same reference angle.
McGraw Hill DVD Teacher Resources 4.1_178_IA
50°
Rotation Angle 50°
Terminal arm is in quadrant I
Positive Coterminal Angles
Counterclockwise
50° + (360°)(1) =
Negative Coterminal Angles
Clockwise
-310°
770°
-670°
410°
50° + (360°)(2) =
50° + (360°)(-1) =
50° + (360°)(-2) =
Math 30-1 9

10. Coterminal Angles in General Form
By adding or subtracting multiples of one full rotation, you
can write an infinite number of angles that are coterminal
with any given angle.
θ ± (360°)n, where n is any natural number
Why must n be a natural number?
Math 30-1 10

11. Sketching Angles and Listing Coterminal Angles
Sketch the following angles in standard position. Identify all coterminal angles
within the domain -720° < θ < 720° . Express each angle in general form.
a) 1500 b) -2400
c) 5700
Positive
Negative
General Form
5100
-2100
1200
-6000
2100
-1500
150 360 ,
n n N
  240 360 ,
n n N
   570 360 ,
n n N
 
Positive
Negative
General Form
Positive
Negative
General Form
, -5700
, 4800
-5100
Math 30-1 11

12. Radian Measure: Trig and Calculus
The radian measure of an angle is the ratio of arc length of a
sector to the radius of the circle.
 
a
r
number of radians =
arc length
radius
When arc length = radius, the
angle measures one radian.
How many radians do you
think there are in one circle?
Math 30-1 12

13. Construct arcs on the
circle that are equal in
length to the radius.
Radian Measure
2 6.283185307...
radians
 
C  2r
arc length  2(1)
http://www.geogebra.org/en/upload/files/ppsb/radian.html
One full revolution is
Math 30-1 13

14. Radian Measure
One radian is the measure of the central angle subtended in a
circle by an arc of equal length to the radius.
2r
r
r

 =
a
r
O r
r s = r
1 radian
 = 1 revolution of 360
Therefore, 2π rad = 3600.
Or, π rad = 1800.
r
  2 rads
Angle
measures
without
units are
considered
to be in
radians.
Math 30-1 14

15. Math 30-1 15

16. 6

3

2


3
2

0
Benchmark Angles
Special Angles
Radians
4

2
1.57
3.14
4.71
6.28
Math 30-1 16

17. Sketching Angles and Listing Coterminal Angles
Sketch the following angles in standard position. Identify all coterminal angles
within the domain -4π < θ < 4π . Express each angle in general form.
a) b) c)
Positive
Negative
General Form
5
2 ,
6
n n N


 
4
2 ,
3
n n N


   10.47 2 ,
n n N

 
Positive
Negative
General Form
Positive
Negative
General Form
5
6
4
3

 10.47
17
6

7
6


19
,
6


2
3
 8
,
3

10
3


4.19
2.1
 , 8.38

Math 30-1 17