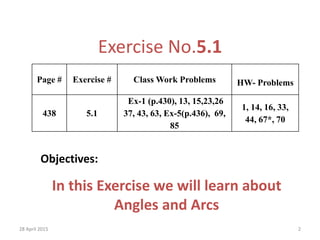
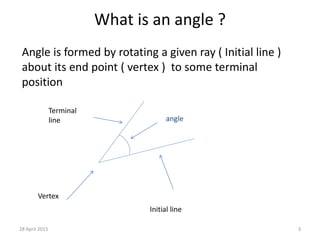
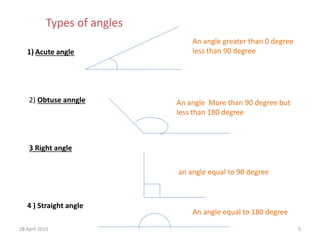
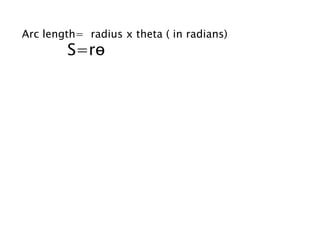1) The document discusses trigonometric functions and angles. It defines angles, units of measurement for angles including degrees and radians, types of angles, and relationships between complementary and supplementary angles. 2) Examples are provided for finding the measure of complementary and supplementary angles. Co-terminal angles are also discussed. 3) The document provides exercises involving converting between degrees and radians, finding measures of angles, determining arc lengths on circles based on central angles and radii, and classifying angles by quadrant.

1. 28 April 2015 1
Math 002
College Algebra and Trigonometry
7th Edition
Module 1
Trigonometric Functions

2. 28 April 2015 2
Exercise No.5.1
28 April 2015 2
Page # Exercise # Class Work Problems HW- Problems
438 5.1
Ex-1 (p.430), 13, 15,23,26
37, 43, 63, Ex-5(p.436), 69,
85
1, 14, 16, 33,
44, 67*, 70
Objectives:
In this Exercise we will learn about
Angles and Arcs

3. What is an angle ?
Angle is formed by rotating a given ray ( Initial line )
about its end point ( vertex ) to some terminal
position
angle
Terminal
line
Initial line
Vertex
28 April 2015 3

4. Unit of Angles
1) Degree 2) Radian
1) Degree: one degree is the 360th part of a
complete circle
2) Radain: Angle At center of the circle made
by the arc whose length is equal to
the radius of the circle
28 April 2015 4

5. 1) Acute angle
2) Obtuse anngle
3 Right angle
4 ) Straight angle
An angle greater than 0 degree
less than 90 degree
Types of angles
An angle More than 90 degree but
less than 180 degree
an angle equal to 90 degree
An angle equal to 180 degree
28 April 2015 5

6. Complementary angle and Supplementary angle
Two positive angle are called Complementary angles if there sum is 900
β
α
α + β = 900
α
β
α + β = 1800
Two positive angle are called supplementary angles if there sum is 1800
28 April 2015 6

7. Example 1 page 430
• For each angle , find the measure (if possible )
of its complement and of its supplement.
• a) θ= 400
• b) θ= 1250

8. Co terminal Angle
• Given ˂ θ in standard position with measure x0
then the measures of the angles that are co
terminal with ˂ θ are given by
28 April 2015 8

9. Questions 13 and 15
Page 438
• Determine the measure of the positive angle
with measure less than 360o that is co-
terminal with the given angle and then classify
the angle by quadrant. Assume the following
angles are in the standard position
• 13 ) 610o 15) -975o
28 April 2015 9

10. Conversion from Radian to Degree
and
From Degree to Radian
• Radian to Degree
• Multiply the Angle by
• Degree to Radian
• Multiply the Angle by
28 April 2015 10

11. Question No 23.
page 439
• Use a Calculator to convert each decimal the
degree measure to its equivalent DMS
measure θ = 3.4020
28 April 2015 11

12. Question No 26.
page 439
• Use a Calculator to convert each DMS
measure to its equivalent decimal degree
measure θ = 630 29’ 42’’
28 April 2015 12

13. Question No 37.
page 439
• Convert the degree measure to exact Radian
measure θ = 4200
28 April 2015 13

14. Question No 43.
page 439
• Convert the radian measure to exact degree
measure θ = 7π/3
28 April 2015 14

15. An arc of a circle is a "portion"
of the circumference of the
circle.
The length of an arc is simply
the length of its "portion" of
the circumference. Actually,
the circumference itself can be
considered an arc length.

16. The radian measure of a central angle of a circle is
defined as the ratio of the length of the arc the angle
subtends, s, divided by the radius of the circle, r.

17. Arc length= radius x theta ( in radians)
S=rɵ

18. Question No 63.
page 439
• Find the measure in radians and degrees of
the central angle of a circle subtended by the
given arc. Round approximate answer to the
nearest hundred.
r = 5.2 centimeters , s = 12.4 centimeters
28 April 2015 18

19. Example-5(p.436)
• Find the length of an arc that subtends a
central angle of 1200 in a circle with a radius
of 10 centimeters .
28 April 2015 19

20. Question No 69.
page 439
• Find the number of radians in revolutions
28 April 2015 20

21. Question No 85.
page 440
• At the time when the earth was 93 million
miles from the sun , you observed through a
tinted glass that the diameter of the sun
occupies an arc of 31’ . Determine, to the
nearest 10 thousand miles , the diameter of
the sun.
93,000,000
31’
28 April 2015 21

22. Example 2
Page 431
• Assume the following angles are in the
standard position. Determine the measure of
the positive angle with measure less than
• 360o that is co-terminal with the given angle
and then classify the angle by quadrant.
• a ) α=350o b) β=-225o c) ϒ=1105o
28 April 2015 22
Reading Example

23. 28 April 2015 23