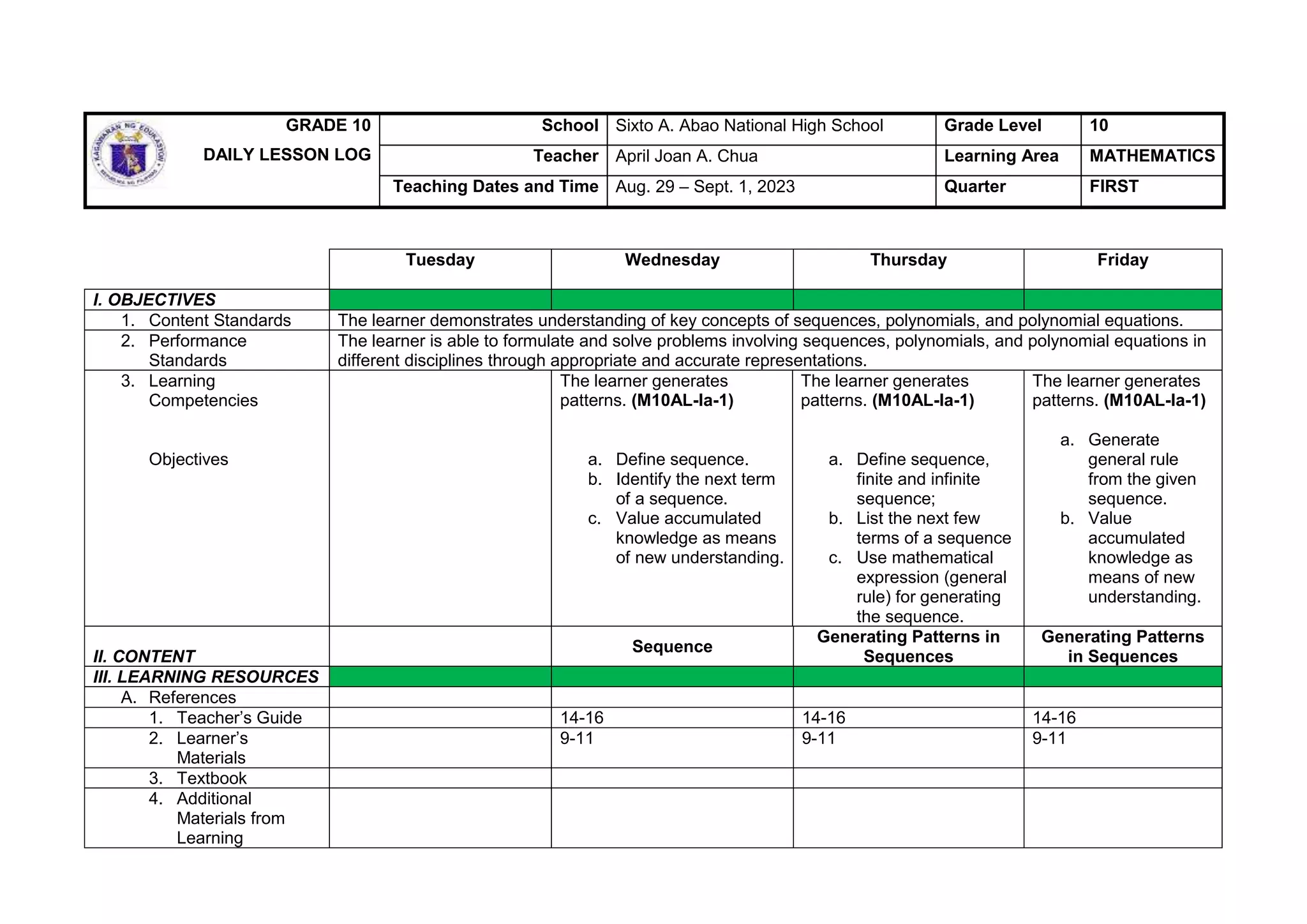
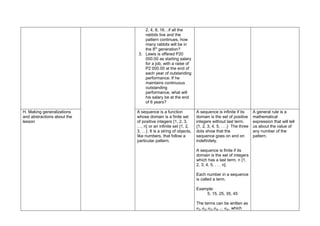
This document contains a daily lesson log for a 10th grade mathematics class. The lesson covers sequences, including defining sequences, identifying patterns in sequences, generating the general rule of a sequence, and solving problems involving sequences. The lesson procedures include reviewing previous concepts, presenting examples of sequences, discussing sequence concepts, practicing identifying patterns and terms, applying sequences to word problems, making generalizations about sequences, and evaluating student learning. The log details the objectives, content, resources, procedures, and reflections for the mathematics lesson on sequences taught over multiple days.

1. GRADE 10
DAILY LESSON LOG
School Sixto A. Abao National High School Grade Level 10
Teacher April Joan A. Chua Learning Area MATHEMATICS
Teaching Dates and Time Aug. 29 – Sept. 1, 2023 Quarter FIRST
Tuesday Wednesday Thursday Friday
I. OBJECTIVES
1. Content Standards The learner demonstrates understanding of key concepts of sequences, polynomials, and polynomial equations.
2. Performance
Standards
The learner is able to formulate and solve problems involving sequences, polynomials, and polynomial equations in
different disciplines through appropriate and accurate representations.
3. Learning
Competencies
Objectives
The learner generates
patterns. (M10AL-Ia-1)
a. Define sequence.
b. Identify the next term
of a sequence.
c. Value accumulated
knowledge as means
of new understanding.
The learner generates
patterns. (M10AL-Ia-1)
a. Define sequence,
finite and infinite
sequence;
b. List the next few
terms of a sequence
c. Use mathematical
expression (general
rule) for generating
the sequence.
The learner generates
patterns. (M10AL-Ia-1)
a. Generate
general rule
from the given
sequence.
b. Value
accumulated
knowledge as
means of new
understanding.
II. CONTENT
Sequence
Generating Patterns in
Sequences
Generating Patterns
in Sequences
III. LEARNING RESOURCES
A. References
1. Teacher’s Guide 14-16 14-16 14-16
2. Learner’s
Materials
9-11 9-11 9-11
3. Textbook
4. Additional
Materials from
Learning

2. Resources (LR)
portal
B. Other Learning
Resources
https://youtu.be/btKkchZRh
zl?si=Kofiu14RAslDe3KM
IV. PROCEDURES
A. Reviewing previous lesson
or presenting the new lesson
Giving of:
 Classroom rules
 Curriculum
overview
 Diagnostic test
Complete the sequence by
supplying the correct
consecutive terms.
1. A, D, G, J, ___, ___, ___
2. 1, 3, 5, 7, ___, ___, ___
3. 1, 4, 9, 16, 25, ___, ___,
___
4. 5, 15, 25, 35, ___, ___,
___
(Answering of
assignment)
B. Establishing a purpose for
the lesson
Draw the next object in each
picture pattern.
Study the sequences given
below.
a) Days of the week:
{𝑆𝑢𝑛𝑑𝑎𝑦, 𝑀𝑜𝑛𝑑𝑎𝑦,
𝑇𝑢𝑒𝑠𝑑𝑎𝑦, . . . ,
𝑆𝑎𝑡𝑢𝑟𝑑𝑎𝑦}
First 10 positive
perfect squares: {1,
4, 9, 16, 25, 36, 49,
64, 81, 100 }
b) Counting numbers:
{1, 2, 3, 4, 5, . . .}
Multiples of 5: {5,
10, 15, 20, 15, . . .}
Given the sequence 5,
12, 19, 26, 33, …, find
the general rule.
C. Presenting
examples/Instances of the
new lesson
The set objects in the priming
activity are called sequences.
Based on the given, what
can you say about the two
sets of sequences?
How would you get the
general term of a
sequence?

3. A sequence is a function
whose domain is a finite set of
positive integers {1, 2, 3, …,
n} or an infinite set {1, 2, 3,
…}. It is a string of objects, like
numbers, that follow a
particular pattern.
Illustrative Example:
Identify if the set of
each object shows a pattern
or not then find the next term.
1.
2. 0, 4, 8, 12, 16, ___...
3. 9, 4, -1, -6, -11,
____
4. 1, 3, 9, 27, 81, _____
5. 160, 80, 40,
20,10, ___
Is there a difference
between them?
D. Discussing new concepts
and practicing new skills # 1
Think Pair Share
Study the following patterns
then supply the missing term
to complete the sequence.
1. Jan, Mar, May, Jul, Sept,
___, ____
2. 5, 8, 11, 14, ___, 20, ___...
A sequence is infinite if its
domain is the set of positive
integers without last term,
{1, 2, 3, 4, 5, . . .} The three
dots show that the
sequence goes on and on
indefinitely.
A sequence is finite if its
domain is the set of integers
Given the sequence 5,
12, 19, 26, 33, …, find
the general rule.
(Teacher explains
solution)

4. 3. 1/2, 1, 3/2, 2, 5/2, ___, 7/2,
4, ___,…
4. 3, -6, ___, -24, 48, ___ …
5. 1, 4, 9, 16, ___, 36, 49, 64,
___
which has a last term, n {1,
2, 3, 4, 5, . . . n}.
Each number in a sequence
is called a term.
Example:
5, 15, 25, 35, 45
The terms can be written as
𝑎1, 𝑎2, 𝑎3, 𝑎4, … 𝑎𝑛, which
means 𝑎1 is the first term,
𝑎2 is the second term, 𝑎3 is
the third term, 𝑎4 is the
fourth term, 𝑎𝑛 is the last
term.
E. Discussing new concepts
and practicing new skills # 2
How do you identify the next
object/number in a
sequence?
Sometimes a pattern in the
sequence can be obtained
and the sequence can be
written using a general
term.
Example 1.
Find the first four terms of
the sequence 𝑎𝑛 = 2𝑛 − 1.
(Teacher shows the
solution)
F. Developing mastery (leads
to Formative Assessment 3)
Find the Number
Study the given sequence,
identify the pattern then find
the missing number.
1. 1 3 5 7 9 ____ 13 15
17
2. 0 5 10 ____ 20
25 30 35 40
Boardwork:
Find the first 5 terms of the
sequence whose general
term is given by 𝑎𝑛 = (𝑛 −
3)𝑛
.
(Student volunteers will
show their answers on the
board)
Find the general rule of
the following
sequences:
1. 1, 4, 9, 16, 25…
2. 3, 4, 5, 6…
3. -1, 1, 3, 5…
4. 2, 4, 8, 16, 32…

5. 3. 17 15 13 ____ 9
7 5 3
4. 25 35 45 ___ 65 75
5. 34 44 54 64 ___ 84
94
G. Finding practical
application of concepts and
skills in daily living
Pair Activity:
Understand the problems
carefully then answer.
1. The table below shows
the cost of renting the
Cavite Hall at Island
Cove Resort and Leisure
Park in Kawit, Cavite
depending on the
number of attendees.
Number
of
Persons
Rental
Cost in
Peso
20 6200
25 6500
30 6800
35 7100
Jose booked the hall for
a birthday party for 40
persons. How much will
he pay?
2. A rabbit population grew
in the following pattern:

6. 2, 4, 8, 16…if all the
rabbits live and the
pattern continues, how
many rabbits will be in
the 8th
generation?
3. Lewis is offered P20
000.00 as starting salary
for a job, with a raise of
P2 000.00 at the end of
each year of outstanding
performance. If he
maintains continuous
outstanding
performance, what will
his salary be at the end
of 6 years?
H. Making generalizations
and abstractions about the
lesson
A sequence is a function
whose domain is a finite set
of positive integers {1, 2, 3,
…, n} or an infinite set {1, 2,
3, …}. It is a string of objects,
like numbers, that follow a
particular pattern.
A sequence is infinite if its
domain is the set of positive
integers without last term,
{1, 2, 3, 4, 5, . . .} The three
dots show that the
sequence goes on and on
indefinitely.
A sequence is finite if its
domain is the set of integers
which has a last term, n {1,
2, 3, 4, 5, . . . n}.
Each number in a sequence
is called a term.
Example:
5, 15, 25, 35, 45
The terms can be written as
𝑎1, 𝑎2, 𝑎3, 𝑎4, … 𝑎𝑛, which
A general rule is a
mathematical
expression that will tell
us about the value of
any number of the
pattern.

7. means 𝑎1 is the first term,
𝑎2 is the second term, 𝑎3 is
the third term, 𝑎4 is the
fourth term, 𝑎𝑛 is the last
term.
I. Evaluating learning Individual activity:
Study the following patterns
then supply the missing term
to complete the sequence.
1. 2, 4, 7, 11, ____
2. 7, 9, 11, ____, ____, 17,
19
3. 1, 8, 27, 64, 125, ____
4. 5, 10, 7, 14, 11, 22, 19,
_____
5. 6, 18, 54, 162, _____
Individual activity:
Find the first 5 terms of the
sequence given the nth
term.
1. 𝑎𝑛 = 𝑛 + 4
2. 𝑎𝑛 = 2𝑛 − 1
Individual activity:
Find the general rule of
the following
sequences:
1. -1, 3, 7, 11…
2. 3, 9, 27, 81…
3. 5, 10, 15, 20…
J. Additional activities for
application or remediation
Assignment #1: Find the
Terms
Use the general rule to find
the first 3 terms of the
sequence:
𝑎𝑛 = 12 − 3𝑛
Review the lesson for
this week and study in
advance about
arithmetic sequence.
V. REMARKS
VI. REFLECTION
A. No. of learners who earned
80% in the evaluation

8. B. No. of learners who require
additional activities for
remediation who scored
below 80%
C. Did the remedial lessons
work? No. of learners who
have caught up with the
lesson
E. Which of my teaching
strategies worked well? Why
did these work?
F. What difficulties did I
encounter which my principal
or supervisor can help me
solve?
G. What innovation or
localized materials did I
use/discover which I wish to
share with other teachers?
Prepared by: Checked:
APRIL JOAN A. CHUA VICENTE V. SABELLINA
SST - I Master Teacher - I
Recommending approval: Approved:
MELODYN U. TABAMO VICTORIANO J. CAPAGNGAN, JR.
Assistant School Principal School Principal