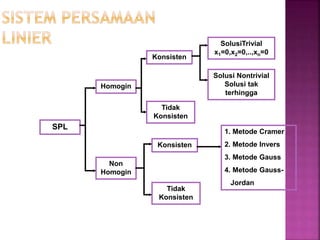
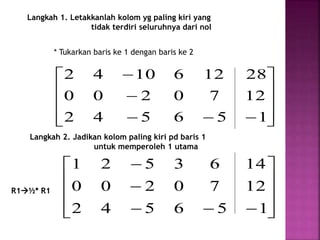
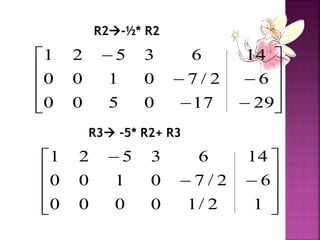
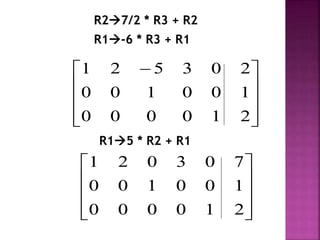
Dokumen ini menjelaskan tentang sistem persamaan linier dan teknik penyelesaiannya menggunakan metode seperti Cramer, invers, Gauss, dan Gauss-Jordan. Ditekankan pentingnya bentuk baris eselon dan tereduksi dalam menyelesaikan sistem persamaan, serta langkah-langkah spesifik untuk mencapai solusi. Hasil akhir menunjukkan sistem tersebut konsisten dengan banyaknya solusi yang tak terhingga.

2. SPL
Homogin
Non
Homogin
Konsisten
Tidak
Konsisten
SolusiTrivial
x1=0,x2=0,..,xn=0
Solusi Nontrivial
Solusi tak
terhingga
Konsisten
Tidak
Konsisten
1. Metode Cramer
2. Metode Invers
3. Metode Gauss
4. Metode Gauss-
Jordan

3.  Bentuk Baris Eselon/Tereduksi
Matriks yang berbentuk baris eselon tereduksi harus
mempunyai sifat - sifat berikut ini :
1. Jika suatu baris tidak seluruhnya terdiri dari nol,
maka angka tak nol pertama dalam baris tersebut
adalah angka 1.
2. Jika ada sebarang baris yang seluruhnya terdiri dari
nol, maka baris - baris ini dikelompokkan di bagian
bawah matriks.
3. Jika sebarang dua baris yang berurutan yang tidak
seluruhnya terdiri dari nol, angka 1 dalam baris yang
lebih bawah terletak di sebelah kanan angka 1 dalam
baris yang lebih atas.
4. Masing - masing kolom yang berisi angka 1,
mempunyai nol di tempat lainnya.

4. Contoh matriks - matriks berikut dalam bentuk
baris eselon tereduksi.


























0
0
0
0
,
1
0
0
0
1
0
0
0
1
,
3
1
0
0
7
0
1
0
4
0
0
1
































5
1
0
0
2
6
1
0
7
3
4
1
,
0
0
0
0
1
0
0
1
1
,
0
0
0
0
4
1
0
0
2
6
1
0
7
3
4
1
Suatu matriks yang mempunyai sifat 1, 2, dan 3 saja (tidak perlu 4) disebut
mempunyai bentuk baris eselon.

5. Selesaikan sistem persamaan dengan
membentuk eselon baris :















1
5
6
5
4
2
28
12
6
10
4
2
12
7
0
2
0
0
Pemecahan Eliminasi Gauss/
Gaus-Jordan :
Merupakan penyelesaian sistem persamaan
Linier yang menghasilkan matriks dalam
bentuk eselon (tangga) baris

6. Langkah 1. Letakkanlah kolom yg paling kiri yang
tidak terdiri seluruhnya dari nol















1
5
6
5
4
2
12
7
0
2
0
0
28
12
6
10
4
2
* Tukarkan baris ke 1 dengan baris ke 2
Langkah 2. Jadikan kolom paling kiri pd baris 1
untuk memperoleh 1 utama















1
5
6
5
4
2
12
7
0
2
0
0
14
6
3
5
2
1
R1½* R1

7. Langkah 3. Tambahkan kelipatan yg sesuai dari
baris atas kepada baris-baris yang dibawah
sehingga entri-entri dibawah 1 utama menjadi nol
R3 -2* R1+ R3














29
17
0
5
0
0
12
7
0
2
0
0
14
6
3
5
2
1
Langkah 4. Sekarang tutuplah baris paling atas,
Ulangi langkah 1, 2, dan 3 untuk baris yang
tersisa.

8. 














29
17
0
5
0
0
6
2
/
7
0
1
0
0
14
6
3
5
2
1
R2-½* R2
R3 -5* R2+ R3













1
2
/
1
0
0
0
0
6
2
/
7
0
1
0
0
14
6
3
5
2
1

9. R32 * R3













2
1
0
0
0
0
6
2
/
7
0
1
0
0
14
6
3
5
2
1
Langkah selanjutnya kita dapat menyelesaikannya dengan substitusi balik
maupun dengan menjadikan bentuk eselon baris yang tereduksi (entri bukan
nol pertama dalam setiap baris)
Proses menggunakan operasi - operasi baris elementer untuk mengubah
suatu matriks menjadi bentuk eselon baris yang tereduksi disebut Eliminasi
Gauss-Jordan
sedangkan prosedur yang hanya menghasilkan bentuk baris eselon disebut
eliminasi Gaussian.

10. R27/2 * R3 + R2









 
2
1
0
0
0
0
1
0
0
1
0
0
2
0
3
5
2
1
R1-6 * R3 + R1
R15 * R2 + R1










2
1
0
0
0
0
1
0
0
1
0
0
7
0
3
0
2
1

11. Kemudian kita memperoleh hasil sbb :
X1+2x2+ 3x4 =7
x3 = 1
x5 = 2
x1= -2x2 - 3x4 + 7 = -2. r – 3. t + 7
X2 = r x4 = t x3 = 1 x5 = 2
Sistem tersebut konsisten dengan tak berhingga
banyaknya pemecahan.