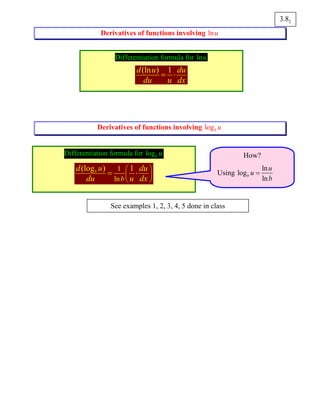
1. This section discusses how to find derivatives of functions involving logarithms, including ln(u) and logb(u). It outlines the differentiation formulas for these functions and explains logarithmic differentiation. 2. Logarithmic differentiation can be used to differentiate functions that involve products, quotients, or powers, by taking the natural log of both sides, simplifying using properties of logarithms, and then differentiating. 3. Logarithmic differentiation is particularly useful for differentiating functions of the form v/u, where both u and v are functions of the variable. Examples are provided.

1. Section 3.8 Derivatives of logarithmic functions
Learning outcomes
After completing this section, you will inshaAllah be able to
1. find derivatives of expressions involving lnu
2. find derivatives of expressions involving logb u
3. explain what is logarithmic differentiation
4. find derivatives using method of logarithmic differentiation
5. differentiate functions of the form v
u
Recall the following properties
which are needed for this section
13.8
• ( )ln ln lnxy x y= +
• ln ln ln
x
x y
y
⎛ ⎞
= −⎜ ⎟
⎝ ⎠
• ( )ln lnr
x r x=

2. Derivatives of functions involving lnu
Derivatives of functions involving logb u
23.8
Differentiation formula for lnu
(ln ) 1d u du
du u dx
= ⋅
Differentiation formula for logb u
1
ln
(log ) 1b
b
d u du
du u dx
⎛ ⎞
⎜ ⎟
⎝ ⎠
= ⋅
How?
Using
ln
log
ln
b
u
u
b
=
See examples 1, 2, 3, 4, 5 done in class

3. How to perform logarithmic differentiation of f(x)?
• We learn more with the help of example.
End of 3.8
33.8
See example 6 done in class
Main idea
• Simplify before differentiating
How?
• Aim: To differentiate y=f(x) (1)
• If f(x) involves products, quotients or powers then
o take ‘ln’ on both sides of (1)
o simplify using properties of ‘ln’
o differentiate after simplification
Suitable when f(x) involves
products, quotients or powers
Important application of logarithmic differentiation
Differentiating functions of the form
v
u where both u and v are functions of x
See examples 7, 8 done in class