More Related Content
DOCX
PPTX
PPTX
PDF
PDF
PPT
PDF
ConvNetの歴史とResNet亜種、ベストプラクティス PPTX
What's hot
PDF
PDF
PDF
PPTX
【DL輪読会】SimCSE: Simple Contrastive Learning of Sentence Embeddings (EMNLP 2021) PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial) PDF
三次元点群を取り扱うニューラルネットワークのサーベイ PDF
Bayesian Neural Networks : Survey PDF
最近強化学習の良記事がたくさん出てきたので勉強しながらまとめた PDF
PDF
[DL輪読会]Reward Augmented Maximum Likelihood for Neural Structured Prediction PDF
PDF
PDF
Rにおける大規模データ解析(第10回TokyoWebMining) PDF
【論文読み会】Deep Clustering for Unsupervised Learning of Visual Features PDF
Deep Learningによる画像認識革命 ー歴史・最新理論から実践応用までー PDF
PPTX
【DL輪読会】Transformers are Sample Efficient World Models PPTX
Deep Recurrent Q-Learning(DRQN) for Partially Observable MDPs PDF
Learning to forget continual prediction with lstm PPTX
ベイズ深層学習5章 ニューラルネットワークのベイズ推論 Bayesian deep learning Similar to [第2版]Python機械学習プログラミング 第11章
PDF
東京都市大学 データ解析入門 8 クラスタリングと分類分析 1 PDF
分類問題 - 機械学習ライブラリ scikit-learn の活用 PDF
PPTX
PDF
PDF
PDF
PPTX
PPTX
データサイエンティストに聞く!今更聞けない機械学習の基礎から応用まで V7 PDF
ユークリッド距離以外の距離で教師無しクラスタリング PPT
Tokyo r#10 Rによるデータサイエンス 第五章:クラスター分析 PDF
PPTX
PDF
PDF
[第2版] Python機械学習プログラミング 第3章(5節~) PDF
第3回集合知プログラミング勉強会 #TokyoCI グループを見つけ出す PDF
PDF
PDF
PDF
データサイエンティストに聞く!今更聞けない機械学習の基礎から応用まで V k-1 More from Haruki Eguchi
PDF
[第2版]Python機械学習プログラミング 第7章 PDF
[第2版] Python機械学習プログラミング 第2章 PDF
[第2版] Python機械学習プログラミング 第4章 PDF
[第2版]Python機械学習プログラミング 第6章 PPTX
[第2版]Python機械学習プログラミング 第10章 PDF
[第2版] Python機械学習プログラミング 第5章 PDF
[第2版]Python機械学習プログラミング 第15章 PDF
[第2版]Python機械学習プログラミング 第14章 PDF
[第2版]Python機械学習プログラミング 第16章 PDF
[第2版] Python機械学習プログラミング 第3章(~4節) PDF
[第2版]Python機械学習プログラミング 第13章 PDF
[第2版] Python機械学習プログラミング 第1章 PPTX
[第2版]Python機械学習プログラミング 第12章 PDF
[第2版]Python機械学習プログラミング 第8章 PPTX
[第2版]Python機械学習プログラミング 第9章 PDF
[第2版]Python機械学習プログラミング 第12章 Recently uploaded
PDF
2025→2026宙畑ゆく年くる年レポート_100社を超える企業アンケート総まとめ!!_企業まとめ_1229_3版 PDF
第21回 Gen AI 勉強会「NotebookLMで60ページ超の スライドを作成してみた」 PDF
100年後の知財業界-生成AIスライドアドリブプレゼン イーパテントYouTube配信 PDF
さくらインターネットの今 法林リージョン:さくらのAIとか GPUとかイベントとか 〜2026年もバク進します!〜 PDF
Starlink Direct-to-Cell (D2C) 技術の概要と将来の展望 PDF
Reiwa 7 IT Strategist Afternoon I Question-1 3C Analysis PDF
PDF
Reiwa 7 IT Strategist Afternoon I Question-1 Ansoff's Growth Vector PPTX
[第2版]Python機械学習プログラミング 第11章
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
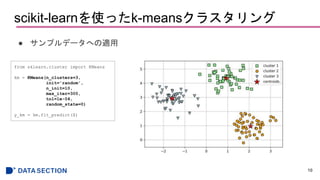
scikit-learnを使ったk-meansクラスタリング
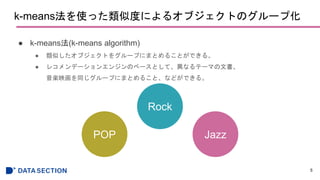
● k-means法を説明するための簡易的な例
● ランダムに生成された150個のサンプル点を用意する。
7
fromsklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
plt.scatter(X[:, 0], X[:, 1],
c='white', marker='o', edgecolor='black',
s=50)
plt.grid()
plt.tight_layout()
plt.show()
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
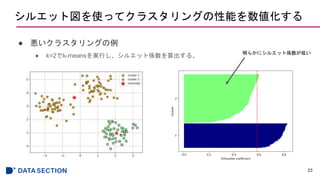
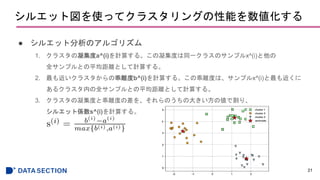
シルエット図を使ってクラスタリングの性能を数値化する
● シルエット係数のプロット
22
from sklearn.metricsimport silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower,y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
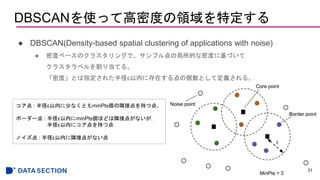
DBSCANを使って高密度の領域を特定する
● DBSCAN(Density-based spatialclustering of applications with noise)
● 密度ベースのクラスタリングで、サンプル点の局所的な密度に基づいて
クラスタラベルを割り当てる。
「密度」とは指定された半径ε以内に存在する点の個数として定義される。
31
コア点 : 半径ε以内に少なくともminPts個の隣接点を持つ点。
ボーダー点 : 半径ε以内にminPts個ほどは隣接点がないが,
半径ε以内にコア点を持つ点
ノイズ点 : 半径ε以内に隣接点がない点
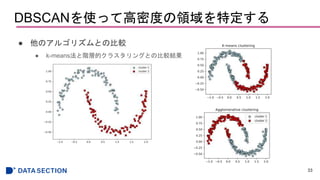
- 32.
- 33.
- 34.
Editor's Notes
- #3 IMDb: Internet Movie Database
- #6 同じグループに属しているオブジェクトは、他のグループに属しているグループよりも�互いに関連度が高い。
- #8 n_samples=サンプル数
n_features=特徴量の個数�centers=クラスタ数�cluster_std=クラスタ内の標準偏差
- #9 セントロイド:類似する点の中心を表す
- #11 n_clusters=クラスタ数
init=セントロイドの初期値をランダムに選択 �n_init=異なるセントロイドの初期値を用いたk-meansの試行回数�max_iter=最大イテレーション回数�tol=1e-04収束判定
- #14 この確率変数を使うと、次に選択されるセントロイドμは、Mにあるセントロイドと距離が離れているところに配置される確率が高くなる。
分母:Mに含まれていないサンプルxとMのセントロイドの距離を2乗したものの最小値を合計したもの
分子:次のセントロイドμとMのセントロイドの距離を2乗したものの最小値
- #16 各セントロイドへの帰属の確率は合計すると1になる。
クラスタメンバシップ確率:該当するクラスタのセントロイドのメンバーとなる確率
- #17 クラスタメンバシップ確率:該当するクラスタのセントロイドのメンバーとなる確率
- #18 クラスタメンバシップ確率:該当するクラスタのセントロイドのメンバーとなる確率
ファジー性が大きいとよりぼやけたクラスタになる。
- #19 k-meansよりも計算コストは高いが、一般的に収束するまでのイテレーション数はFCMの方が少ない。
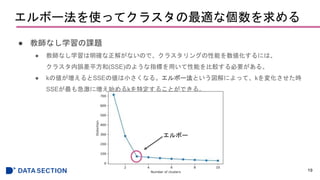
- #20 kの値が増えるとSSEの値は小さくなる。 -> サンプルがそれぞれが属するクラスタのセントロイドに近づくから。
- #22 シルエット係数の範囲は-1, 1
乖離度と凝集度が等しいとシルエット係数は0
b>>aの場合は理想的なシルエット係数である1に近づく
- #23 縦軸が全サンプル
横軸がシルエット係数。
クラスタごとにクラスタ内のサンプルのシルエット係数が小さいものからプロットしている。
赤い点線は全サンプルのシルエット係数の平均。
- #24 縦軸が全サンプル
横軸がシルエット係数。
クラスタごとにクラスタ内のサンプルのシルエット係数が小さいものからプロットしている。
赤い点線は全サンプルのシルエット係数の平均。
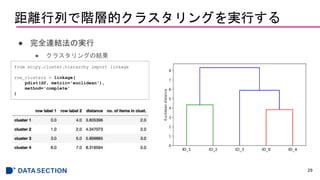
- #29 類似度が低い:最も離れている
距離行列の計算はscipyのspatial.distanceモジュールのpdist関数を使用
- #30 scikit-learnでも実装可能
AgglomerativeClusteringクラス
- #36 k-meansよりも計算コストは高いが、一般的に収束するまでのイテレーション数はFCMの方が少ない。
![Python機械学習プログラミング
読み会
第11章
クラスタ分析 - ラベルなしデータの分析
1
[第2版]
基盤 江口春紀](https://image.slidesharecdn.com/11-181212011918/85/2-Python-11-1-320.jpg)




![scikit-learnを使ったk-meansクラスタリング
● k-means法を説明するための簡易的な例
● ランダムに生成された150個のサンプル点を用意する。
7
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
plt.scatter(X[:, 0], X[:, 1],
c='white', marker='o', edgecolor='black',
s=50)
plt.grid()
plt.tight_layout()
plt.show()](https://image.slidesharecdn.com/11-181212011918/85/2-Python-11-7-320.jpg)











![シルエット図を使ってクラスタリングの性能を数値化する
● シルエット係数のプロット
22
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower,y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)](https://image.slidesharecdn.com/11-181212011918/85/2-Python-11-22-320.jpg)