社内勉強会で使用した資料です。

1. Python機械学習プログラミング
読み会
第13章
ニューラルネットワークのトレーニングをTensorFlowで並列化
1
[第2版]
基盤 江口春紀

2. 目次
● TensorFlowとトレーニングの性能
● TensorFlowの高レベルAPI：
ニューラルネットワークの効率的なトレーニング
● 多層ニューラルネットワークでの活性化関数の選択
2

3. 3
TensorFlowとトレーニングの性能

4. TensorFlowとトレーニングの性能
● 高負荷の処理を行う上での課題
● 複数のコアに分散させて並列で処理をする。
● CPUよりGPUの方が有利だがGPUをターゲットとしたコードの記述が必要。
4

5. TensorFlowの学び方
● TensorFlowの低レベルAPI
5
>>> import tensorflow as tf
>>>
>>> g = tf.Graph()
>>> with g.as_default():
... x = tf.placeholder(dtype=tf.float32,shape=(None), name='x')
... w = tf.Variable(2.0, name='weight')
... b = tf.Variable(0.7, name='bias')
... z = w*x + b
... init = tf.global_variables_initializer()
...
>>> with tf.Session(graph=g) as sess:
... sess.run(init)
... for t in [1.0, 0.6, -1.8]:
... print('x=%4.1f --> z=%4.1f'%(t, sess.run(z, feed_dict={x:t})))
...
x= 1.0 --> z= 2.7
x= 0.6 --> z= 1.9
x=-1.8 --> z=-2.9

6. TensorFlowの学び方
● TensorFlowの低レベルAPI(配列構造の操作)
6
>>> import numpy as np
>>>
>>> g = tf.Graph()
>>> with g.as_default():
... x = tf.placeholder(dtype=tf.float32,
... shape=(None, 2, 3), name='input_x')
... x2 = tf.reshape(x, shape=(-1, 6), name='x2')
... xsum = tf.reduce_sum(x2, axis=0, name='col_sum')
... xmean = tf.reduce_mean(x2, axis=0, name='col_mean')
...
>>> with tf.Session(graph=g) as sess:
... x_array = np.arange(18).reshape(3, 2, 3)
... print('input shape: ', x_array.shape)
... print('Reshaped:n', sess.run(x2, feed_dict={x:x_array}))
... print('Column Sums:n',sess.run(xsum, feed_dict={x:x_array}))
... print('Column Means:n',sess.run(xmean, feed_dict={x:x_array}))
input shape: (3, 2, 3)
Reshaped:
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[ 12. 13. 14. 15. 16. 17.]]
Column Sums:
[ 18. 21. 24. 27. 30. 33.]
Column Means:
[ 6. 7. 8. 9. 10. 11.]

7. TensorFlowを使った単純なモデルの開発
● 最小二乗線形回帰(Ordinary Least Squares linear regression)
● 右下のグラフに示す 1次元のデータセットを使い、入力 xから出力yを予測する
線形回帰モデルをトレーニングする。
7

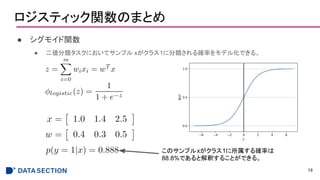
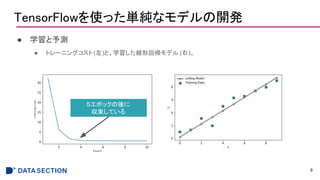
8. TensorFlowを使った単純なモデルの開発
● 実装
● 線形回帰モデルをz=wx+bと
定義した後、コスト関数として
平均二乗誤差(MSE)を定義する。
● 重みパラメータの学習には、
勾配降下法のオプティマイザを
使用する。
8
def build(self):
self.X = tf.placeholder(dtype=tf.float32,
shape=(None, self.x_dim),
name='x_input')
self.y = tf.placeholder(dtype=tf.float32,
shape=(None), name='y_input')
w = tf.Variable(tf.zeros(shape=(1)), name='weight')
b = tf.Variable(tf.zeros(shape=(1)), name="bias")
self.z_net = tf.squeeze(w*self.X + b, name='z_net')
sqr_errors = tf.square(self.y - self.z_net,
name='sqr_errors')
self.mean_cost = tf.reduce_mean(sqr_errors,
name='mean_cost')
optimizer = tf.train.GradientDescentOptimizer(
learning_rate=self.learning_rate,
name='GradientDescent')
self.optimizer = optimizer.minimize(self.mean_cost)

9. TensorFlowを使った単純なモデルの開発
● 学習と予測
● トレーニングコスト(左)と、学習した線形回帰モデル (右)。
9
５エポックの後に
収束している

10. 10
TensorFlowの高レベルAPI

11. TensorFlowの高レベルAPI
11
Layers API

12. TensorFlowの高レベルAPI
● MNISTデータセットを使った手書き文字の分類
● トレーニングデータセット： 60,000サンプル
● テストデータセット：10,000サンプル
12

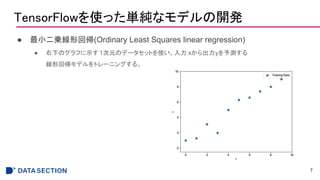
13. Layers APIを使って多層ニューラルネットワークを構築する
● Layers APIによる実装
13
import tensorflow as tf
n_features = X_train_centered.shape[1]
n_classes = 10
random_seed = 123
np.random.seed(random_seed)
g = tf.Graph()
with g.as_default():
tf.set_random_seed(random_seed)
tf_x = tf.placeholder(dtype=tf.float32, shape=(None, n_features), name='tf_x')
tf_y = tf.placeholder(dtype=tf.int32, shape=None, name='tf_y')
y_onehot = tf.one_hot(indices=tf_y, depth=n_classes)
h1 = tf.layers.dense(inputs=tf_x, units=50, activation=tf.tanh, name='layer1')
h2 = tf.layers.dense(inputs=h1, units=50, activation=tf.tanh, name='layer2')
logits = tf.layers.dense(inputs=h2, units=10, activation=None, name='layer3')
predictions = {
'classes' : tf.argmax(logits, axis=1, name='predicted_classes'),
'probabilities' : tf.nn.softmax(logits, name='softmax_tensor')
}
activationで
活性化関数を指定する
ただLayerを重ねていくだけで良い

14. Kerasを使って多層ニューラルネットワークを構築する
● Keras
● Pythonで書かれた，TensorFlowまたはCNTK，Theano上で実行可能な
ニューラルネットワークライブラリである。
● 非常に少ないコードでニューラルネットワークを実装することができる。
14

15. Kerasを使って多層ニューラルネットワークを構築する
● Kerasによる実装
15
y_train_onehot = keras.utils.to_categorical(y_train)
model = keras.models.Sequential()
model.add(
keras.layers.Dense(units=50, input_dim=X_train_centered.shape[1],
kernel_initializer='glorot_uniform', bias_initializer='zeros', activation='tanh'))
model.add(
keras.layers.Dense(units=50, input_dim=50, kernel_initializer='glorot_uniform',
bias_initializer='zeros', activation='tanh'))
model.add(
keras.layers.Dense(units=y_train_onehot.shape[1], input_dim=50, kernel_initializer='glorot_uniform',
bias_initializer='zeros', activation='softmax'))
sgd_optimizer = keras.optimizers.SGD(lr=0.001, decay=1e-7, momentum=.9)
model.compile(optimizer=sgd_optimizer, loss='categorical_crossentropy')
history = model.fit(X_train_centered, y_train_onehot, batch_size=64, epochs=50,
verbose=1, validation_split=0.1)
one-hotフォーマット変換
.add()で簡単にレイヤーを積み重ねることができる
モデルの初期化

16. 16
多層ニューラルネットワークでの
活性化関数の選択

17. 多層ニューラルネットワークでの活性化関数の選択
● 活性化関数には非線形関数を使用する
● 多層ニューラルネットワークでは微分可能であれば、どのような関数でも活性化関数に
使用することができるが、線形関数を用いるとニューラルネットワークで層を深くすること
の意味がなくなる。
これは、線形関数の総和は線形関数であるため。
17

18. ロジスティック関数のまとめ
● シグモイド関数
● 二値分類タスクにおいてサンプル xがクラス1に分類される確率をモデル化できる。
18
このサンプルxがクラス1に所属する確率は
88.8%であると解釈することができる。

19. 双曲線正接関数
● 双曲線正接(Hyperbolic tangent)関数
● ロジスティック関数の尺度を取り直したバージョンとして解釈できる。
● ロジスティック関数に対する双曲線正接関数の利点は出力範囲が広く、
開区間(-1, 1)に及ぶことである。
19

20. ReLUで勾配消失問題に対処する
● 勾配消失問題
● 例えば総入力がz1=20からz2=25に変化したとき
のように出力はあまり変わらないことがわかる。
つまり活性化関数の微分は zが大きくなると
消失してしまう。
● ReLU(Rectified Linear Unit)
● ReLUは勾配消失問題に対処し、以下のように
定義される。
20

21. まとめ
● TensorFlow
● DLをメインに数値計算を行うオープンソースライブラリで、
多層ニューラルネットワークの定義とトレーニングを効率よく行うことができる。
● TensorFlowの高レベルAPI
● Layers API
● Keras
● 活性化関数
● シグモイド関数、双曲線正接関数、 ReLU、等。
21