1. Батлагдсан хэрчмүүдийн тухай теорeм
[a, b] ,[a2, b2], ….[an, bn] өгөгдсөн байг.
n үед an≤ an+1≤ bn+1≤ bn
Өөрөөр хэлбэл: [a, b] [a2, b2] ….. [ an+1, bn+1 ] биелэгдэхээс гадна,
уг хэрчмүүдийн утгын дараалал {[ bn-an]}→ 0 байвал {[ an, bn]}
батлагдсан хэрчмийн дараалал гэж хэлнэ.
Теором 3.5: Батлагдсан хэрчмийн дараалал {[ an, bn]} –ийн бүх
хэрчмүүдэд харъяалагдах цэг ≠ цорын ганц байна.
Баталгаа: Өгөгдсөн an≤ an+1 ба bn+1≤ bn =>{[ an, bn]} хэрчмүүдийн зүүн
цэгүүд an дараалал нь үл буурах , баруун талын цэгүүдийн дараалал нь
үл өсөх дараалал үүсгэх ба an≤ b1 ба bn≥ а1 нөхцлүүд биелэгдэнэ.Иймд
3.2 теором ѐсоор {an }→c' {bn}→c″ хязгааруудад нийлнэ. 0=
an)= lim - lim →∞an= c'- c″ учир c'= c″ байна.
Иймд {an }, {bn} –дарааллууд ерөнхий c'= c″ = c хязгаар руу нийлэх ба n
утганд an≤ c≤ bn биелэгдэнэ.Иймд с- цэг нь бүх [ an, bn] хэрчимд
харъяаагдана.
Дарааллын хязгаарыг олох чухал жишээ
а >1 бол
Баталгаа: n , n >0 гэе. Тэгэхэд ( Бернулын тэнцэтгэл биш
n
(1+x) > 1+nx n≥2, x>-1 , x≠ 0 );
n
Бернулын тэнцэтгэл биш ѐсоор а= (1+ n ) > 1+n n , 0< n< болох
ба теором 3.1 ѐсоор n=0 байна.Иймд
Функцийн хязгаар
1. f(x)- функцийн x→x0 үеийн хязгаар гэж: f(x) =b
2. f(x)- функцийн x0 цэг баруун хязгаар f(x)= f(x)= b'
=f( )

2. 3. f(x)- функцийн x0 цэг дээрх зүүн хязгаар : f(x)= f(x)= b″
=f( )
4. f(x)- функцийн төгсгөлгүй цэг дээрх буюу x→ үеийн хязгаар гэж :
f(x) = с
5. f(x)- функцийг + цэг дээрх буюу x→ үеийн хязгаар гэж :
f(x) = с'
6. f(x)- функцийг - цэг дээрх буюу x→ үеийн хязгаар гэж :
f(x) = с″
7. f(x)- функцийн x0 цэг дээрх төгсгөлгүй хязгааруудыг : f(x) = ,
f(x) =+ , f(x) =- гэх мэт.
F(X) функцийн x→x0 үеийн хязгаар
Def: (Гейнe). Хэрэв X- олонлогийн {Xn} – цэгүүдийн x0 –руу нийлэх
Жишээ нь: а) =1 в) (1+x)
Критерий Коши: (Зарчим)
f(x)- ийн x=a цэг дээрх төгсөглөг хязгаар оршин байх нь зөвхөн хэрэв
>0 тоо авахад = ( )> 0 олдоод х' , х''є Х (X-f(x)-ийн тодорхойлогдох
муж) хувьд
| х'- а |<
| х''- а |< биелэгдэж байх үед
|f(х') – f(х'') |< биелэх явдал юм.
Жнь: f(x)= counts= с функц нь тоон шулууны Х0 цэг бүр дээр с хязгаартай
байна. Учир нь {Xn}→ Х0 авахад f(x)=c иймд f(x)=с болно.
Def: (Гейнe) Хэрэв Х-олонлогийн {Xn} цэгүүдийн Х0 –руу нийлэх
дараалалд харгалзах
у= f(x) функцийн утгуудийн дараалал {yn =f(Xn)} нь ямар нэг b тоо руу
нийлж байвал энэ b – тоо f(x)-ийн функцийн х→x0 үеийн (эсвэл (x= x0)
дээрх хязгаар гэнэ.)

3. f(x)=b (Xn≠X0)
Функцийн Х= Х0 дээрх хязгаарын дүрмүүд
f(x)=a ба g(x)=b бол:
1) [f(x) ± g(x)] = a ± b= f(x) + g(x)
2) =const, [ = *a= f(x)
3) [f(x) * g(x)] = a * b= [f(x)] [ g(x)]
4) Хэрэв g(x)≠0 ба b≠0 бол = =
5) Хэрэв f(x)= a , g(x)= b ба f(x)≤ g(x) f(x)≤ g(x)
6) x≠x0 үед f(x)= g(x) ба g(x)=b => f(x)= g(x)
7) f(x), g(x), (x) –функцууд Х-олонлог дээр тодорхойлогдсон байг.
f(x)= g(x)=b бөгөөд f(x)≤ (x)≤ g(x), (нь ядаж x≠x0 үед)
биелж байвал:
(x)=b болно.
8) Давхар функцийн хязгаар
Хэрэв у=f(u)- функц u= (x) функцуудын утгын муж дээр
тодорхойлогдсон Давхар функц у=f[ (x)] өгөгдсөн гэж үзээд:
Хэрэв (x)=u0 ба f(u)=f(u0)
(x)]= f(u)=f(u0)
n n-1
Жнь: Рn (x) =a0x + a1x + ….. + an-1x+an функцийн ямар нэг Х0
дээрх хязгаар :
lim Рn (x) = [a0xn + a1xn-1 + ….. + an-1x+an ]= a0xn + a1xn-1 + ….+
an-1x+an ]= Рn (x0)

4. Өрөөсгөл хязгаарууд
Хэрэв Х {xn}→ x0 ба xn> x0 байх дараалалд харгалзах y=f(x)
функцийн утгуудын дараалал {y=f(xn)}→ b' хязгаартай байвал b' тоог f(x)-
ийн x=x0 цэг дээрх баруун өрөөсгөл хязгаар гэнэ.
Эндээс f(x)= f(x)= b' =f(x ) гэж бичнэ.
Яг ийм байдлаар f(x)=y –ийг x=x0 цэг дээрх зүүн өрөөсгөл хязгаар
f(x)= f(x)= b″ =f(x ) тодорхойлогдоно.
Жнь: f(x)= (x≠0) (sgnx)
1) x>0 үед f(x)= + 1
2) x<0 үед f(x)= - 1
Иймд f(x)= +1 , (x)= - 1 болно.
Дээр дурдсан хязгаарын дүрмүүдэд зохих өөрчлөлтүүдийг хийж
өрөөсгөл хязгаарын дүрмүүдийг гаргаж авна.
Жнь: f(x)= b' ба g(x)= c' бол f(x) ± g(x)] = b' ± c'=
f(x)± g(x)
f(x)-функцийн x=x0 дээрх хязгаар оршин байх <=> нь x0 цэг дээрх
баруун, зүүн өрөөсгөл хязгаарууд хоѐул оршдог бөгөөд хоорондоо
тэнцүү байх явдал юм.
f(x)= f(x)= f(x)
x→ , x→+ , x→- үеийн хязгаар
(Төгсгөлгүй алсын цэг дээрх хязгаар)
Хэрэв y=f(x) функцийн тодорхойлогдох муж Х-олонлогийн цэгүүдээс
тогтсон төгсгөлгүй их {xn} дараалалд харгалзах функцийн утгуудын
дараалал {yn= f(xn)}→ c хязгаар руу нийлж байвал , y=f(x) функцийн
x→ үеийн хязгаар нь с тоо гэж хэлэх ба энэ нөхцөлд:
f(x)= с гэж бичнэ.

5. Үүнтэй адилаар : Хэрэв y=f(x) функцийн тодорхойлогдох муж Х { xn }→+
(Х { xn }→ - )
байх { xn }дараалалд харгалзах функцийн утгуудын дараалал
{yn= f(xn)}→ c' , (yn= f(xn)}→ c'')
байвал: f(x)= с' , ( f(- )) гэж бичнэ.
Хэрэв f(x)= с => f(x)= с=> f(x)= с
Төгсгөлгүй хязгаар
Хэрэв Х { xn }→ байх дарааллын харгалзах y=f(x) функцийн
утгуудын дараалал
{yn= f(xn)}→
Эсвэл {yn= f(xn)}→ +
{yn= f(xn)}→ - байвал x=x0 цэг дээр f(x) төгсгөлгүй хязгаартай
гэх ба f(x)= , эсвэл f(x)=+ , эсвэл f(x)= - гэж бичнэ.
Хэрэв y=f(x) функцийн x=x0 цэг дээрх хязгаар төгсгөлгүй байна.х→ x0
үед y=f(x) нь төгсгөлгүй хэмжигдэхүүн гэж бас нэрлэдэг.
(Энд x0 =± , x0 = байж болно.)
Хязгаарын тодорхойлолт , хязгаарын дүрмүүдээс:
1) Хэрэв f(x)=b , g(x)= => [f(x) + g(x)] = +
2) Хэрэв f(x)=b , g(x)= => =0
3) Хэрэв lim f(x)= b> 0, lim g(x)= 0 ба Х0-ийн орчинд g(x)>0 бол
=+
Тасралтгүй функц
Хэрэв Х { xn }→ дараалал авахад f(x)=f(x0) байвал f(x) функц
x=x0 цэг дээр

6. тасралтгүй гэж нэрлэнэ.Х-олонлог дээр y=f(x) тодорхойлогдсон бөгөөд
Х x0 нь Х-олонлогын хязгаарын цэг байг.Хэрэв f(x)=f(x0) байвал
f(x) функц x=x0 дээр тасралтгүй гэж хэлнэ.
Def: = ( )>0 бөгөөд | x- x0 |< байх бүх утгуудад |f(x)- f(x0)|<
бол f(x)- нь x=x0 дээр тасралтгүй гэнэ.
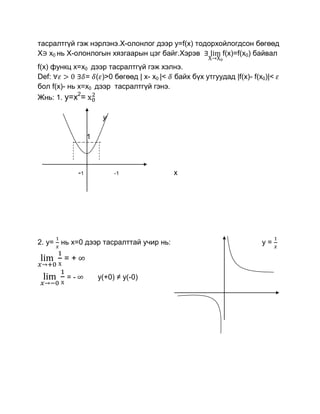
2
Жнь: 1. y=x =
y
1
-1 -1 x
2. y= нь х=0 дээр тасралттай учир нь: y=
=+
=- у(+0) ≠ y(-0)

7. 3. y нь 0-дээр тасралттай , хэрэв xn = (n=1,
2, 3…..)
дараалал авбал xn→0 ба энэ дараалалд харгалзах y=y(x) –функцийн
утгууд:
{-1, 1, -1, 1, ….} cална.
y=
x=x0 цэг дээрх функцийн хязгаарын дүрмүүд
Хэрэв f(x)=а , g(x)=b бол
1. [f(x) + g(x)] = a± b = f(x) + g(x)
2. , [ f(x)]= *a = * f(x)
3. [f(x) * g(x)] = a* b = [ f(x)] * [ g(x)]
4. Хэрэв g(x)≠0 ба b≠0=> = =
5. Хэрэв f(x) ≤ g(x) => f(x) ≤ g(x)
6. x=x0 үед f(x)= g(x) ба g(x)= b байвал f(x)= g(x)= b
7. Хэрэв f(x) , g(x), (x) –функцууд Х-дээр тодорхойлогдсон.

8. f(x)= g(x)= b бөгөөд f(x) ≤ g(x) ≤ (x) ядаж (х≠х0 ) үед биелэж
байвал : (x)=b
байна.
8. Давхар функцийн хязгаар:
Хэрэв y=f(u) Функц u= (x) функцийн утгын муж дээр
тодорхойлогдсон y=f[ (x)] –өгөгдсөн гэж үзье.Тэгэхэд (x) –
u0 ба f(u)= f(u0) биелж байвал :
(x)] = f(u)= f(u0) эдгээр дүрмүүд нь яг ижилхэн арга
зарчмаар батлагдана.
Жнь: Рационоль функц R(x)= , байхад
R(x) = = = R(x)
Өрөөсгөл хязгаарууд
Хэрэв Х {Хn}→X0 ба Хn >X0 байх дурын дараалалд харгалзах y=f(x) –
ийн утгуудын дараалал yn=f(xn)→b' хязгаартай байвал b' –тоон y=f(x)
функцийн x=x0 дээрх баруун өрөөсгөл хязгаар гэж нэрлэх ба :
f(x)= f(x)= b' =f( ) гэж бичнэ.
Яг үүнтэй адилханаар: Зүүн өрөөсгөл хязгаар гэж:
f(x)= f(x)= b″ =f( ) –гэж тодорхойлно.
Төгсгөлгүй алсын цэг дээрх хязгаар
Хэрэв y=f(x) функцийн тодорхойлогдох муж Х-олонлогийн цэгүүдээс
тогтсон төгсгөлгүй их дараалал {Xn} дараалалд харгалзах функцийн
утгуудын дараалал f(Xn)→c хязгаар руу
Жнь: 1. y=x2 функцийн х аргументын бүх утгуудад тасралтгүй
2. y= нь функцийн х=0 дээр тасралттай яагад гэвэл :

9. =+ ; =-
Тасралтгүй функц дээрх үйлдлүүд
Функцийн өгөгдсөн цэг дээрх хязгаарын дүрмүүдээс тасралтгүй
функцууд дээрх үйлдлүүдийн үр дүнгийн тухай дараахь дүгнэлтээс шууд
гарна.
1).Хэрэв f(x) , g(x) нь x=x0 дээр тасралтгүй бол
1. [f(x) ± g(x)]
2. хувьд [ ]
3. [f(x) * g(x)]
4. Хэрэв g(x₀)≠0 байвал –функцууд тасралтгүй x=x0 дээр
байна.
2). Хэрэв f(x) функцд x=x0 дээр тасралтгүй байвал давхар функц h(x)=
g[f(x)] нь x=x0 дээр тасралтгүй байна.
Тасралтын цэгүүдийн ангилал , засагдах тасрал
f(x) функц нь x=x0 дээр тасралтгүй байх шалтгаан нь дараах
үзэгдлүүдийн аль нэгэн юм.
1) x0 –цэг дээр өрөөсгөл хязгаарууд f(x0-0) , f(x+0) оршин байхгүй
байх.
2) x0 –цэг дээр өрөөсгөл хязгаарууд төгсгөл биш байх.
3) x0 –цэг дээр өрөөсгөл хязгаарууд хоорондоо тэнцүү биш байх:
f(x0+0) ≠ f(x0-0)
4) x0 –цэг дээр өрөөсгөл хязгаарууд хоорондоо тэнцүү боловч f(x0)
утгатай тэнцүү биш: f(x0+0) = f(x0-0)≠ f(x0)
1. Тодорхой бус цэг
2. Үсрэлтийн цэг (Төгсгөлгүй )
3. Үсрэлтийн цэг
4. Засагдах , засрагдах тасралтын цэг гэж нэрлэнэ.
Мөн 3., 4. тохиолдлуудыг хамтад нь I төрлийн тасралтын цэг, 1., 2.
тохиолдлуудыг нь II төрлийн тасралтын цэг гэж ангилдаг.
Хэрэв x0 –нь f(x)-ийн Үсрэлтийн цэг бол [f(x0+0) - f(x0-0)] –тоон f(x)-
функцийн засагдах тасралтын цэг бол f(x) функцийн x=x0 цэг дээрх

10. утгыг өөрчлөх замаар f(x)-функцийн x=x0 цэг дээр тасралтгүй функц
байхаар тодорхойлж болно.
Жнь:f(x)= нь x=0 цэг дээр тодорхойлогдоогүй , гэвч =1
Ийм f(0)=1 гэж авбал,
f(x) = нь тоон бүх шулуун дээр тасралтгүй болно.
f(x0+0)
f(x0-0) x0 x0 x0
x0
f(x0)
f(x0-0)
f(x0+0)
x0
a) үсрэлт б) төгсгөлгүй үсрэлт в) зааглагдах тасралт
Үндсэн Элементар функцуудийн тасралтгүй чанар
Энд тасралтгүй функцуудын тодорхойлолтыг шалгаж батлана.
1. y=e
2. y=x
h
3. y=x
4. y=p(x)=a0+a1x1+…+anxn p(x) =p(x0)
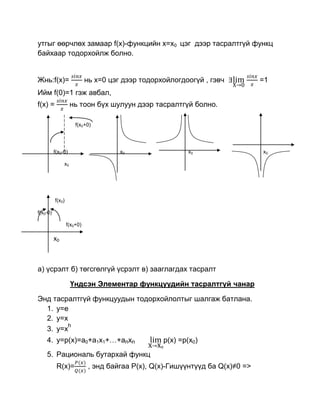
5. Pациональ бутархай функц
R(x)= , энд байгаа P(x), Q(x)-Гишүүнтүүд ба Q(x)≠0 =>

11. R(x)= = =R(x0)
6. Зэрэгт функц y=xa , a>0 , x≥ 0 мужинд тодорхойлогдсон тасралтгүй.
h
7. Илтгэгч функц: y=ax (a>0) Үүнийг шалгая. =
h
lim =
8. f(x) (a>0 , a≠0 , x>0)
9. Тригонометрийн функцууд:
y=sinx
y=cosx
10. tgx –нь cosx≠0 –ээс бусад бүх цэгүүд дээр тасралттай:
x= , , …, xn=
–ээс бусад дээр
ctg x=± n-ээс бусад бүх цэгүүд дээр тасралтгүй байна.
Хэрчим дээр тасралтгүй функцийн гол чанарууд
Теорема1:.[a, b]-хэрчим дээр тасралтгүй y=f(x) функцийн утгуудын
дотор хамгийн их ба хамгийн бага тоо ямагт оршино.
d
а
C b
m

12. Геометр утга:Энэ нь f(x) нь [a,b] хамгийн их ба хамгийн бага утгуудыг
агуулах нийт с ба d цэгүүд [a, b] хэрчимд оршино гэсэн үг. ( m≤ f(x)≤ M)
Теорема2: [a , b] –дээр тасралтгүй f(x) функц энэ хэрчмийн үзүүрийн
цэгүүд дээр харилцан эсрэг тэмдэгтэй утгуудыг авдаг. (f(a)<0, f(b)>0 )
бол f(x)-нь 0-тэй тэнцүү утгыг хүлээн авдаг цэг [a.b] хэрчим дээр
олдно.Хэрэв [a.b] хэрчим дээр тасралтгүй функцийн хамгийн их утга нь
M хамгийн бага утга бол m бол энэ 2 тооны хооронд орших аливаа L1
(m< L1<M ) тоотой тэнцүү утгыг функц хүлээн авна.
Теорема3: [a.b] хэрчим дээр f(x) тасралтгүй функц бол [a , b] x'x''
цэгүүдийн хувьд | x'x''|→0 бол f(x')- f(x'')→0
Дифференциал тоолох функцийн уламжлал
Def: y=f(x) –функцийн x0 цэгийн орчинд тодорхойлогдсон ба Х-энэ орчны
дурын цэг гэе.
Хэрэв = f '(x0) , (f '(x0)< )
x- x0= X гэе. Мөн X=h гэе.
f(x)-f(x0)= f(x0+ X) – f(x0)
f(x0)= f(x0+ X) – f(x0) эдгээрийг ашиглавал:
f '(x0)= =
уламжлалуудыг бас , , y' гэх мэт тэмдэглэдэг.
Жнь: y=x2
Энэ тохиолдолд : у = (x+ x)2-x2= 2x· x+( x)2 = x2+2 x2+( x)2-x2= 2 x·x+
x2
Эндээс =
Эндээс y'= = 2x+ x= 2x
1.c=const c'=0
n n-1
2. y=x (n>1) функцийн уламжлал : y'= n ·x
(Уламжлалын тодорхойлолтонд орж байгаа хязгаарын оронд “өрөөсгөл
хязгаар”-ын авч үзэх замаар өрөөсгөл уламжлалын ойлголтонд хүрдэг.)

13. Тухайлбал: f(x)=y Функцийн x=x0 цэг дээрх зүүн өрөөсгөл уламжлал:
(x0) = ;
Баруун өрөөсгөл:
(x0) = гэж тодорхойлогдоно.
Хязгаар ба өрөөсгөл хязгааруудын холбоог тогтоосон дүгнэлтийн
адилаар
Хэрэв өгөгдсөн цэг дээрх уламжлал оршин байвал өрөөсгөл
уламжллууд 2-уулаа оршин байх ба тэнцүү утгатай байна.Буцаагаад
өрөөсгөл уламжллууд 2-уул оршин байдаг ба тэнцүү бол уламжлал
оршин байдаг гэдгийн тогтоож байна.)
Уламжлалын физик утга
Ямар нэг замын дагуух цэгийн хөдөлгөөнийг авч үзье.
Хөдөлгөөн эхэлсэн цаг мөчөөс хойш t-хугацаанд цэшийн явж өнгөрсөн
замыг S=f(x) , Тэгэхэд цаг хугацааны завсарт явж өнгөрүүлсэн замын
хэмжээ s=f(t+ t)- f(t) байх ба – нь t хугацааны завсарт дахь
дундаж хурд болно.
Иймд – нь t→0 үеийн хязгаар = = S'(t)
нь t-агшин дахь цэгийн хөдөлгөөний хурд байна.
V= S'(t) = хурдатгал нь а =
Уламжлалын дүрмүүд
Уламжлал ба арифметик үйлдлүүд
Хэрэв u(x) ба (x) функцийн Х цэг дээрх уламжлалууд оршиж байвал:
Нийлбэр [u(x) + (x)]
=const бол [u(x)]
[u(x)] · [ (x)]
Хэрэв (x)≠ 0 бол [ ] функцуудийн уламжлал нь бас оршин байх
бөгөөд

14. 1) [u(x) ± (x)]' = u'(x) ± (x)
2) [ u(x)]'= u'(x)
3) [u(x) · (x)]' = u'(x) (x) + u(x)· (x)
4) [ ]' =
Баталгаа:
1. = + ;
тэнцэтгэлд h→0 үед хязгаарыг шилжвэл гарна.
2. = ; = u'(x);
3. = +
= + u(x)
h→0 үед хязгаарыг шилжвэл 3) гарна.
4. [ - ]= [ ]=
= ·
[ - u(x) ; h→0 үед хязгаарыг
шилжвэл 4) гарна.
Давхар функцийн уламжлал
Хэрэв y=f(u) ба u= (x)-ээр y=f( (x)) тодорхойлогдсон бөгөөд
байгуулагч функцуудын уламжлал (u) ба (x) нь тасралтгүй
функцууд бол давхар функцийн уламжлал нь оршиг байх ба
=f(u)· = · эсвэл = [u(u)]· = ·
Жнь: y=(5+2x-3x2)10 , -?
9
Энд u= 5+2x-3x2 гэж байвал y=u10 ба = 10· u , = 2-6x=>
=10(5+2x-3x2)9 · (2-6x)

15. Урвуу функцийн уламжлал
Хэрэв монотон функц y=f(х) нь Х-цэг дээр төгсгөлөг бөгөөд 0-тэй
тэнцүү биш уламжлалтай байвал уруу функц x= (y) нь харгалзах у
дээр уламжлалтай байх ба (y)= , эсвэл = байна.
Баталгаа: f(x)-фугкцийн х≠0 өөрчлөлтөнд түүнд харгалзах
функцийн утгын өөрчлөлт нь ( монотон чанарын үндсэн дээд ) у≠0
байна.
Тэгэхэд: = ба х→0 үед y→0 байх нөхцлийг ашиглаж
хязгаарт шилжвэл:
(y)= = = ;
Жнь: y=f(x)= (x>0)
y2=x учраас уруу функц x= (y) = y2
Иймд (y)=2y байх учраас урвуу функцийн уламжлалын томъѐо
ѐсоор:
= = = болно.
Параметр тэгшитгэлүүдээр өгөгдсөн функцийн уламжлал
f(t), .. (t)- нь t-ээс хамаарах тасралтгүй уламжлалтай функцууд ба х=
{f(t) , y= (t)} системээр тодорхойлогдсон у=y(x) функцийн
уламжлалыг олъѐ.
f '(t) ≠0 , x=f(t) –ийн урвуу функц оршин байдаг гэж t= (t) үзье.
Тэгвэл функц уламжлалын томъѐо ѐсоор: '(х) = ; ба у=f(x)=
(t)]- давхар функцийн уламжлал : '(х) = '(х) (t)] · '(t)=>
'(х) = = ( )
Жнь: x={ a(1-t) , y=a } a

16. Системээс у=y(x) функцд тодорхойлогдоно гэж үзвэл :
= = = = -1
Үндсэн элементар функцууд
Тригонометрийн функцууд:
1) Y=sinx нь х өөрчлөлт авахад : =sin(x+ х)* sinx=2sin
cos(x+ ) хэлбэртэй болно.
Эндээс: y' = lim = · lim
cos(x+ )= 1·cosx=>sinx=cosx
2) Үүнтэй төстэйгөөр: cos'x=-sinx
3) tg'x= '= = =
= => tg'x = ( )
4) Мөн ctg'x= ( )
5) y= arcsinx-ийн урвуу функц X=siny ба уруу функцийн уламжлал
томъѐо ѐсоор:
= = = = = => arcsinx=
(-1<x<1)
6) Мөн адилаар:
arccosx=- (-1<x<1)
7) y=arctgx авахад түүний урвуу функц x=tgy' ба урвуу функц томъѐо
ѐсоор: = = = = = ;=> arctg'x =
8) Мөн адилаар: arcctg'x = -

17. Дээд эрэмбийн уламжлал ба дифференциал
y=f(x) Функцийн I эрэмбийн уламжлал f '(x)-нь х-ээс хамаарсан функц
байх учир энэ f '(x)-ийн уламжлал нь f(x) –ийн II эрэмбийн уламжлал гэж
нэрлэдэг.
Г.м III, IV , n –эрэмбийн уламжлалуудыг тодорхойлно.
n
y(II), y(III), y(IV), ….y(n) эсвэл f (x), ….f
(n)
(x) мөн , , …… гэж
тэмдэглэнэ.
Дээд эрэмбийн уламжлал нь:
(n) (n-1)
f (x) [f (x)]' n>1 тодорхойлогдоно.
(0)
f (x)=f(x) Дээд эрэмбийн уламжлалын дэс дараалал
дифференциалчлагдах аргаар бодож гаргана.
Зарим ерөнхий томъѐо:
(n)
1) y= , = бол у = =
(n+m) (n) (m)
2) y (x) [y (x)] n,m N
(n) n (n)
3) Хэрэв y=ax+b , a,b=const бол y =a * f ( ax+b)
(n) (n- m)
4) Лейбницийн томъѐо: [ ] = u (x)*
N=2 , [ ]'' =[ ]'= =[ ]' =
Жнь:
n-1 n
1) y= бол у'= x , y''= ( ) ,…..y = ( )… (
)
2) y=cosx , y'=-sinx , y''= -cosx , y'''=sinx ;
n (n)
y = cosx =cos( x+ n )
(2m)
хэрэв n=2m =>y =cos(2m) x=(-1) m cosx
n=2m+1=> y(2m+1) =cos(2m+1) x=(-1) m+1 sinx