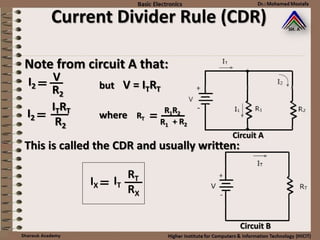
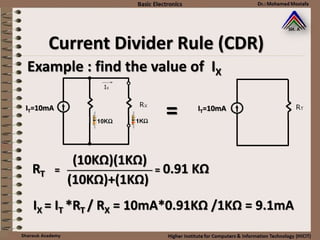
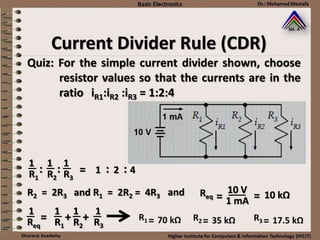
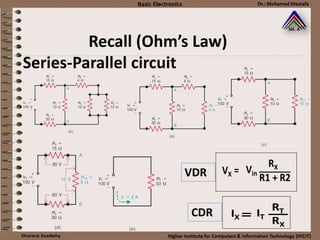
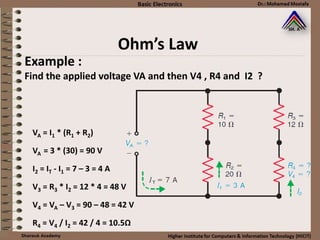
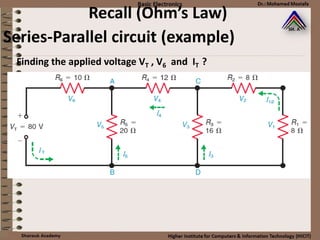
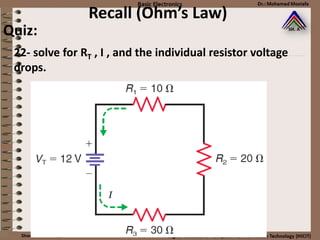
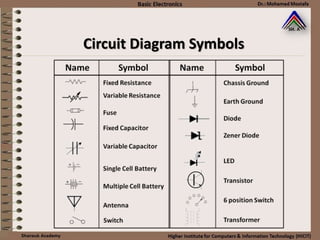
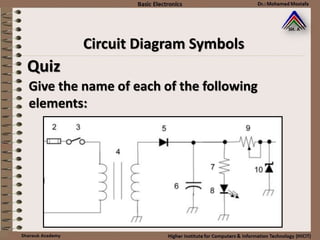
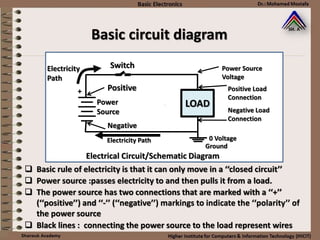
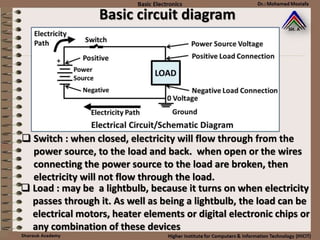
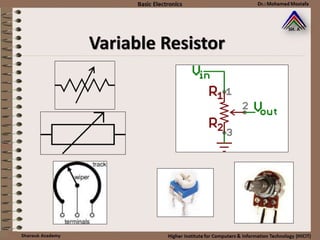
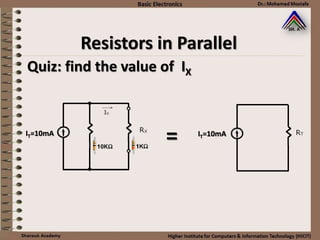
This document provides information about basic circuit diagram symbols and components. It begins with an overview of basic circuit diagrams showing a power source, switch, and load. It then discusses passive electronic components like resistors and capacitors. Resistors are described in detail, including color codes, types, and how resistors behave in series and parallel circuits. Ohm's law and applications like voltage dividers and current dividers are also covered.

1. Circuit Diagram Symbols

2. Quiz
Give the name of each of the following
elements:
Circuit Diagram Symbols

3. Basic circuit diagram
 Basic rule of electricity is that it can only move in a ‘‘closed circuit’’
 Power source :passes electricity to and then pulls it from a load.
 The power source has two connections that are marked with a ‘‘+’’
(‘‘positive’’) and ‘‘-’’ (‘‘negative’’) markings to indicate the ‘‘polarity’’ of
the power source
 Black lines : connecting the power source to the load represent wires
`
Switch
Electricity Path
Positive
Negative
Power
Source
+
Electricity
Path
Electrical Circuit/Schematic Diagram
Ground
LOAD
Power Source
Voltage
Positive Load
Connection
Negative Load
Connection
0 Voltage

4. Basic circuit diagram
 Switch : when closed, electricity will flow through from the
power source, to the load and back. when open or the wires
connecting the power source to the load are broken, then
electricity will not flow through the load.
 Load : may be a lightbulb, because it turns on when electricity
passes through it. As well as being a lightbulb, the load can be
electrical motors, heater elements or digital electronic chips or
any combination of these devices

5. Passive electronic components
 A passive electronic component will
typically absorb energy without create any
active gain.
 These are some of the common passive
electronic components.
 Resistor
 Capacitor

6.  A resistor is the most simple electronic component.
 It resists the flow of current through a circuit.
 The end result is a voltage drop (loss in potential) and
power being absorbed within the device.
 Every electrical device, cable or connection has resistance in
it, but for most circuits the resistance within the wiring can
be ignored.
 The resistance is measured in ohms (Ω) and varies from only
a few ohms (or even less if you are considering the normal
cabling) to many mega ohms (MΩ).
 A resistor is normally a small cylindrical device which has
different colored bands indicating the resistance value. For
more details see the resistor color code scheme.
Resistor

7. Resistor color codes
 Resistors are normally labeled using 4 colored
bands across the body of the resistor.
 This consists three bands together indicating
the resistance value of the resistor (ohms) and
 The forth, further away than the first three, is
used to indicate the tolerance (accuracy) of
the resistor.
 Some resistors have a 5th band indicating the
failure rate of the resistor required for military
use.
The bands relate to the resistance as follows:
1st band - first significant figure of resistor value
2nd band - second significant figure of resistor value
3rd band - decimal multiplier (applied against first two bands)
4th band - tolerance (if not present tolerance is 20%)

8. The example above has colors: Red, Green, Blue ... Silver.
This translates to 2 (red), 5 (green), x106 (blue), with a
tolerance of 10%. which is 25,000,000Ω or 25MΩ.
Color Codes

9. Resistors Types

10. Surface Mounted Resistors
R3 = K3 = .3 Ω
1R3 = 1K3 = 1.3 Ω
123 = 12000 Ω = 12 KΩ
122 = 1200 Ω = 1.2 KΩ
121 = 120 Ω = .12 KΩ
654 = 650000 Ω = 650 KΩ
068 = ?

11. Variable Resistor

12. A light dependent resistor (LDR), sometimes called
a photoresistor is a special kind of resistor whose
resistance varies depending upon the amount of
light on it's exposed surface.
Different LDRs can have different properties, but a
typical one may have a resistance measured in KΩ
when in bright light to MΩ when dark.
Light dependent resistor (LDR)

13.  The relationship can be written three ways:
Where:
I …. is the current in amps
V …. is the voltage in volts
R ….. is the resistance in ohms (Ω)
Ohm's Law
 V = I x R
 I = V / R
 R = V/I
 Ohm’s Law rel/ates Current (I), Voltage (E)
and Resistance (R)
RV

14. Resistors in series
Consider circuit A with
two resistor R1, and R2
connected in series
And consider an
equivalent circuit B
with one resistor RT
Circuit A
Circuit B

15. Resistors in series
=
Circuit A Circuit B
VT = V1 + V2
VT = IR1 + IR2 By Ohm’s Law= VT = IRT
But for equivalent circuits, I is the same for circuit A
and circuit B:
Thus VT = IR1 + IR2 = IRT
Yielding RT = R1 + R2

16. Resistors in series
 The equivalent total resistance for resistors
in series is simply the sum of the individual
resistors
RT = R1 + R2 + R3 + ….. Rn
=

17. Resistors in series
Q: What happens when one series resistor is much
larger than the others?
A: The big Resistor wins

18. Resistors in series
RT = 10KΩ + 100KΩ = 110KΩ
I
I
I = V/RT = 10V/110KΩ = 91 mA
VX = I * RX = 91mA * 100KΩ = 9.1V
Example : find the value of VX

19. Resistors in series
Quiz: find the equivalent total series resistance RT
1MΩ
1KΩ
1Ω
30KΩ
45KΩ
60KΩ

20. Resistors in Parallel
Consider circuit A with
two resistor R1, and R2
connected in parallel
And consider an
equivalent circuit B
with one resistor RT
Circuit BCircuit A

21. Resistors in Parallel
=
But V is the same for circuit A and circuit B.
Circuit BCircuit A
By Ohm’s Law= IT = V/RT
IT = I1 +I2
IT = V/R1 +V/R2
Thus IT = V/R1 +V/R2 = V/RT
Yielding 1/RT = 1/R1 +1/R2

22. Resistors in Parallel
 The equivalent total resistance for resistors
in parallel is given by the formula:
1 1 1 1 1
RT R1 R2 R1 Rn
── = ── + ── + ── + . . . ──

23. Resistors in Parallel
Note: For only two resistors in parallel,
1 1 1 R1 + R2
RT R1 R2 R1 R2
── = ── + ── = ─────────
R1 + R2
R1 R2
RT = ─────────OR

24. Resistors in Parallel
Q: What happens when one parallel resistor is
much smaller than the others?
A: The little resistor wins

25. Resistors in Parallel
Example : find the value of IX
(10KΩ)+(1KΩ)
(10KΩ)(1KΩ)
RT = ──────────────── = 0.91 KΩ
V
+
-
V = I x RT = 10mA x .91KΩ = 9.1V
+
-
IX = V/1KΩ = 9.1V/1KΩ = 9.1mA
V

26. Resistors in Parallel
Quiz: find the value of IX
IT=10mAIT=10mA
=

27. Resistors in Parallel
Quiz: Find the equivalent total parallel
resistance RT
1MΩ
1KΩ
1Ω

28. Vout = IR2 = R2 = Vin
R1 + R2
Vin
R1 + R2
R2
Voltage Divider Rule (VDR)

29. Vout = IR2 = R2 = Vin
R1 + R2
Vin
R1 + R2
R2
Voltage Divider Rule (VDR)
The Voltage Divider Rule (VDR) states that the
voltage across an element in a series circuit is
equal to the resistance of the element or
divided by the total resistance of the series
circuit and multiplied by the main input voltage

30. 1) What if R1 goes to infinity? Output voltage is zero.
2) What if R1 goes to 0? Output voltage is equal to the input voltage.
3) What happens if R1=R2? Output voltage is half the input voltage.
4) What if R2 = 2R1? Two-thirds of input voltage.
5) R2 = 9R1? Nine-tenths of input voltage
6) VOUT is closest to the voltage at the other end of the lower-valued
resistor.
Extreme cases:
Vout = IR2 = R2 = Vin
R1 + R2
Vin
R1 + R2
R2
Voltage Divider Rule (VDR)

31. Implementation
Example: Calculate the necessary resistance values to give this
multi-range voltmeter the ranges indicated by the selector
switch positions:
R1
Rcoil = 1 KΩ
F.S.= 50 μA
2 V
Voltage Divider Rule (VDR)

32. Implementation
For voltage range 2 V:
Maximum volt measured by the meter = Vcoil
Vcoil = Rcoil * F.S. = [1*(103)] * [50 *(10-6)]
= 0,05 V
VR1 = input volt range – Vcoil
= 2 – 0.05 = 1.95 V
R1 = VR1 /I
= 1.95 V / F.S. = 1.95/50*10-6 = 39 KΩ
Voltage Divider Rule (VDR)

33. Implementation
Voltage Divider Rule (VDR)
Example: Calculate the necessary resistance values to give this
multi-range voltmeter the ranges indicated by the selector
switch positions:

34. Implementation
For voltage range 25 V:
Maximum volt measured by the meter = Vcoil
Vcoil = Rcoil * F.S. = [1*(103)] * [50 *(10-6)]
= 0,05 V
VR1 = input volt range – Vcoil
= 25 – 0.05 = 24.95 V
R1 = VR1 /I
= 24.95 V / F.S. = 24.95/50*10-6 = 500 KΩ
Voltage Divider Rule (VDR)

35. Implementation
Voltage Divider Rule (VDR)
Example: Calculate the necessary resistance values to give this
multi-range voltmeter the ranges indicated by the selector
switch positions:

36. Implementation
For voltage range 25 V:
Maximum volt measured by the meter = Vcoil
Vcoil = Rcoil * F.S. = [1*(103)] * [50 *(10-6)]
= 0,05 V
VR1 = input volt range – Vcoil
= 100 – 0.05 = 99.95 V
R1 = VR1 /I
= 99.95 V / F.S. = 99.95/50*10-6 = 2 mΩ
Voltage Divider Rule (VDR)

37. Current Divider Rule (CDR)
Note from circuit A that:
VI2
R2
but V = ITRT
ITRTI2
R2
R1R2
RT
R1 + R2
where
This is called the CDR and usually written:
Circuit A
Circuit B

38. The Current Divider Rule (CDR) states that the
current through one of two parallel branches is
equal to the equivalent resistance of the two
parallel resistances divided by the resistance of
the that branch and multiplied by the total
current entering the two parallel branches
Current Divider Rule (CDR)
Circuit A Circuit B

39. Example : find the value of IX
(10KΩ)+(1KΩ)
(10KΩ)(1KΩ)
RT = ──────────────── = 0.91 KΩ
IX = IT *RT / RX = 10mA*0.91KΩ /1KΩ = 9.1mA
Current Divider Rule (CDR)
IT=10mAIT=10mA
=

40. Quiz: For the simple current divider shown, choose
resistor values so that the currents are in the
ratio iR1:iR2 :iR3 = 1:2:4
1
R2
1
R1
1
R3
: : 21 4: :=
1
R2
1
R1
1
R3
1
Req
+ +=
R2 = 2R3 and R1 = 2R2 = 4R3 and Req
10 V
1 mA= = 10 kΩ
Current Divider Rule (CDR)

41. The Short-Circuit
Consider a resistor whose value is zero ohms.
An equivalent representation of such a
resistance, called a short-circuit, is shown
below:
By Ohm’s Law: V = Ri = 0i = 0 Volt

42. The Open-Circuit
Consider a resistor having infinite resistance.
An equivalent representation of such a
resistance, called an open-circuit, is shown
below:
By Ohm’s Law: i = V/R = V/∞ = 0 A

43. Recall (Ohm’s Law)
Series-Parallel circuit
VDR
CDR

44. Ohm’s Law
Example :
Find the applied voltage VA and then V4 , R4 and I2 ?
VA = I1 * (R1 + R2)
I2 = IT - I1 = 7 – 3 = 4 A
V4 = VA – V3 = 90 – 48 = 42 V
V3 = R3 * I2 = 12 * 4 = 48 V
R4 = V4 / I2 = 42 / 4 = 10.5Ω
VA = 3 * (30) = 90 V

45. Recall (Ohm’s Law)
Series-Parallel circuit (example)
Finding the applied voltage VT , V6 and IT ?

46. Recall (Ohm’s Law)
Series-Parallel circuit (example)
- I3 through R3 =
a. 9 mA. b. 15 mA.
c. 6 mA. d. 45 mA.
- If R4 shorts, the voltage, VAB
a. increases. b. decreases.
c. stays the same. d. increases to 24 V.
- If R2 shorts,
a. the voltage, VAB, decreases to 0 V.
b. the total current, IT, flows through R3 .
c. the current, I3 , in R3 is zero.
d. both a and c.
- If R3 becomes open, what happens to the voltage across points A & B?
a. It decreases. b. It increases.
c. It stays the same. d. none of the above.

47. Report
Based on the following readings (15 tests given in the table), for each
test which component is defective and what type of defect is it?
Recall (Ohm’s Law)

48. Recall (Ohm’s Law)
Quiz:
a. different in each resistor.
b. the same everywhere.
c. the highest near the positive and negative terminals of the
voltage source.
d. different at all points along the circuit.
1- In a series circuit, the current, I , is
a. the largest voltage drop.
b. the smallest voltage drop.
c. more current than the other resistors.
d. both a and c.
2- In a series circuit, the largest resistance has

49. Recall (Ohm’s Law)
Quiz:
a. the direction of current through the resistor.
b. how large the resistance is.
c. how close the resistor is to the voltage source.
d. how far away the resistor is from the voltage source.
3- The polarity of a resistor’s voltage drop is determined by
a. 90 V.
b. 30 V.
c. 120 V.
d. It cannot be determined.
4-A voltage of 120 V is applied across two resistors, R 1
and R 2 , in series. If the voltage across R 2 equals 90 V,
how much is the voltage across R 1 ?

50. Recall (Ohm’s Law)
Quiz:
a. decreases.
b. stays the same.
c. increases.
d. drops to zero.
5- If a resistor in a series circuit is shorted, the series
current, I ,
a. 138 Ω.
b. 62 Ω .
c. 26 Ω .
d. It cannot be determined.
6- 56Ω and 82Ω resistor are in series with an unknown
resistor. If the total resistance of the series combination
is 200 Ω, what is the value of the unknown resistor?

51. Recall (Ohm’s Law)
Quiz:
a. infinite (∞) Ω.
b. 0 Ω .
c. RT is much lower than normal.
d. none of the above.
7- How much is the total resistance, RT , of a series circuit if
one of the resistors is open?
a. Each good resistor has the full value of applied voltage.
b. The applied voltage is split evenly among the good resistors.
c. 0 V.
d. It cannot be determined.
8- If a resistor in a series circuit becomes open, how much
is the voltage across each of the remaining resistors that
are still good?

52. Recall (Ohm’s Law)
Quiz:
a. the 5 Ω resistor.
b. the 10 Ω resistor.
c. It depends on how much the current is.
d. They will both dissipate the same amount of power.
9- A 5Ω and 10 Ω resistor are connected in series across a DC
voltage source. Which resistor will dissipate more power?
a. PT = P1 P2 P3 · · · etc.
b. PT = VT l.
c. PT = l2 RT .
d. all of the above.
10- Which of the following equations can be used to
determine the total power in a series circuit?

53. Recall (Ohm’s Law)
Quiz:
11- State three rules for the current, voltage, and resistance
in a series circuit.
12-For a given amount of current, why does a higher
resistance have a larger voltage drop across it?
13- Two 300-W, 120-V lightbulbs are connected in series
across a 240-V line. If the filament of one bulb burns open,
will the other bulb light? Why? With the open circuit, how
much is the voltage across the source and across each
bulb?
14- Prove that if VT = V1 + V2 + V3 , then RT = R1 + R2 + R3 .

54. Recall (Ohm’s Law)
Quiz:
15- In a series string, why does the largest R dissipate the
most power?
16- Give one application of series circuits.
17- a) how much is the current, I , at each of the following
points? - Point A - Point B - Point C
- Point D - Point E - Point F
b) If R1 and R3 are interchanged,
how much is the current, I , in
the circuit?
c) how much is the current, I ,
through each of the following
resistors? - R1 - R2 - R3

55. 18-
19-
20-
21-

56. Recall (Ohm’s Law)
22- solve for RT , I , and the individual resistor voltage
drops.
Quiz:

57. Recall (Ohm’s Law)
23- Assume that the series circuit has failed. When troubleshooting
the circuit the voltmeter record the following resistor voltage drops:
V1 = 0 V, V2 = 0 V, V3 = 24 V, V4 = 0 V
Based on these voltmeter readings, which component is defective
and what type of defect is it? (Assume that only one component is
defective.)
Quiz:

58. Recall (Ohm’s Law)
24- Assume that the series circuit has failed. When troubleshooting
the circuit the voltmeter record the following resistor voltage drops:
V1 = 8 V, V2 = 6.4 V, V3 = 9.6 V, V4 = 0 V
Based on these voltmeter readings, which component is defective
and what type of defect is it? (Assume that only one component is
defective.)
Quiz:

59. Recall (Ohm’s Law)
25- Assume that the series circuit has failed. When troubleshooting
the circuit the voltmeter record the following resistor voltage drops:
V1 = 8 V, V2 = 6.4 V, V3 = 9.6 V, V4 = 0 V
Based on these voltmeter readings, which component is defective
and what type of defect is it? (Assume that only one component is
defective.)
Quiz:

60. Recall (Ohm’s Law)
26- suppose that the ammeter M1 reads 16 A instead of 20 A as it
should. What could be wrong with the circuit?
Quiz:

61. Recall (Ohm’s Law)
27- How many 120Ω resistors must be connected in parallel to
obtain an equivalent resistance , REQ , of 15Ω?
a. 15.
b. 8.
Quiz:
28- Two lightbulbs in parallel with the 120-V power line are rated at
60 W and 100 W, respectively. What is the equivalent resistance , R
EQ , of the bulbs when they are lit?
a. 144 . b. 90 .
c. 213.3 . d. It cannot be determined.