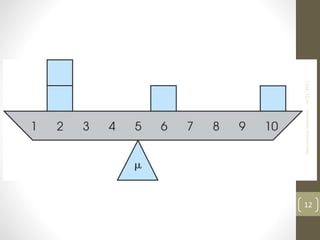
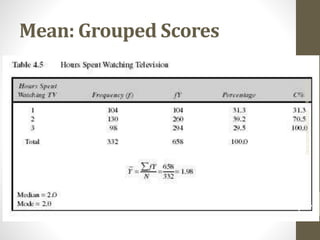
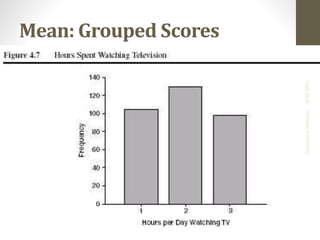
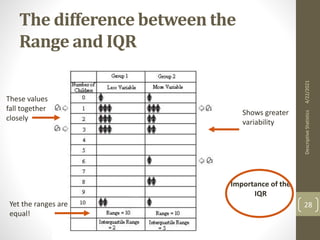
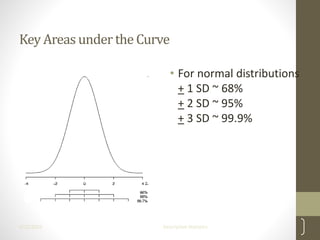
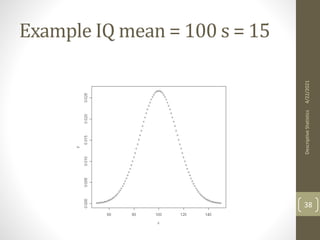
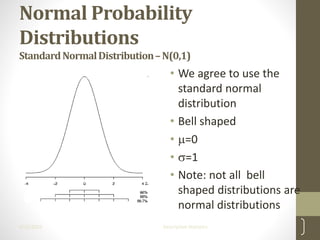
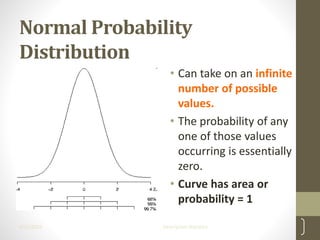
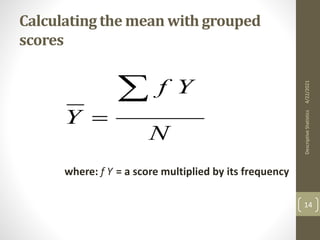This document provides an overview of descriptive statistics concepts including measures of central tendency (mean, median, mode), measures of dispersion (range, IQR, variance, standard deviation), and the normal distribution. It defines these concepts, provides formulas for calculating them, and examples of interpreting different distributions based on these measures. The key points covered are calculating and comparing different central tendency and dispersion measures, and how the normal distribution describes a symmetrical, bell-shaped curve that is important in statistical analysis.