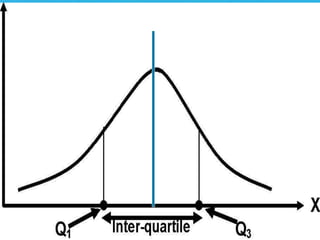
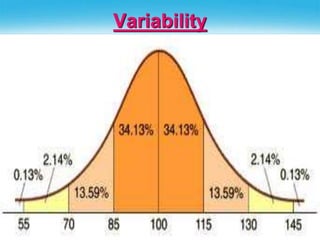
The document discusses various measures of central tendency and variability used in descriptive statistics. It defines the mean as the sum of all values divided by the number of values. The median is the middle value when values are sorted in ascending order. The mode is the most frequently occurring value. Variability measures the dispersion of scores around the mean and includes the range, interquartile range, standard deviation, and variance. The interquartile range is the difference between the third and first quartiles. Covariance measures how two variables vary together and is used to calculate the correlation coefficient. Factors like extreme scores, sample size, stability under sampling, and open-ended distributions can affect measures of variability.

1. CHAPTER 3
Descriptive
Statistics
Measures of
Central Tendency
1

2. Descriptive Statistics
Measures of Central Tendency
 Mean--------Interval or Ratio scale Polygon
– The sum of the values divided by the number of
values--often called the "average." μ=ΣX/N
– Add all of the values together. Divide by the number
of values to obtain the mean.
– Example:
X
7
12
24
20
19
????
2

3. Descriptive Statistics
The Mean is:
μ=ΣX/N= 82/5=16.4
(7 + 12 + 24 + 20 + 19) / 5 =
16.4.
3

4. The Characteristics of Mean
 1. Changing a score in a distribution will
change the mean
 2. Introducing or removing a score from
the distribution will change the mean
 3. Adding or subtracting a constant from
each score will change the mean
 4. Multiplying or dividing each score by a
constant will change the mean
 5. Adding a score which is same as the
mean will not change the mean
4

5. Descriptive Statistics
 Measures of Central Tendency
 Median/MiddleOrdinal ScaleBar/Histogram
– Divides the values into two equal halves, with
half of the values being lower than the median
and half higher than the median.
 Sort the values into ascending order.
 If you have an odd number of values, the
median is the middle value.
 If you have an even number of values, the
median is the arithmetic mean (see above) of
the two middle values.
– Example: The median of the same five numbers
(7, 12, 24, 20, 19) is ???.
5

6. Statistics
 The median is 19.
 Mode-Nominal Scale Bar/Histogram
–The most frequently-occurring value (or
values).
Calculate the frequencies for all of the
values in the data.
The mode is the value (or values) with
the highest frequency.
–Example: For individuals having the
following ages -- 18, 18, 19, 20, 20, 20, 21,
and 23, the mode is ???? The Mode is 20
6

7. CHARACTERISTICS OF MODE
 Nominal Scale
 Discrete Variable
 Describing Shape
7

8. The Range
 The Range:
The Range is the difference between
the highest number –lowest number +1
2, 4, 7, 8, and 10 -> Discrete Numbers
2, 4.6, 7.3, 8.4, and 10 -> Continues
Numbers
The difference between the upper real
limit of the highest number and the
lower real limit of the lowest number.

9. CHAPTER 4
Variability
9

10. 10

11. Variability
Variability is a measure of
dispersion or spreading of
scores around the mean, and
has 2 purposes:
1. Describes the distribution
Next slide
11

12. Range, Interquartile Range, Semi-Interquartile
Range, Standard Deviation, and Variance are the
Measures of Variability
 The Range:
The Range is the difference between the
highest number –lowest number +1
2, 4, 7, 8, and 10 -> Discrete Numbers
2, 4.6, 7.3, 8.4, and 10 -> Continues
Numbers
The difference between the upper real
limit of the highest number and the lower
real limit of the lowest number.

13. Variability
 2. How well an individual score (or
group of scores) represents the
entire distribution. i.e. Z Score
 Ex. In inferential statistics we
collect information from a small
sample then, generalize the results
obtained from the sample to the
entire population.
13

14. Interquartile Range (IQR)
In descriptive statistics, the
Interquartile Range (IQR),
also called the midspread or
middle fifty, is a measure of
statistical dispersion, being
equal to the difference
between the upper and lower
quartiles. (Q3 − Q1)=IQR 14

15. 15

16. 16

17. 17

18. Interquartile Range (IQR)
IQR is the range covered
by the middle 50% of the
distribution.
IQR is the distance
between the 3rd Quartile
and 1st Quartile.
18

19. Semi-Interquartile Range (SIQR)
SIQR is ½ or half of
the Interquartile
Range.
SIQR = (Q3-Q1)/2
19

20. Variability
20

21. 21

22. Variability
Range, SS, Standard Deviations and Variances
 X σ² = ss/N Pop
1 σ = √ss/N
2
4 s² = ss/n-1 or ss/df Standard deviation
5 s = √ss/df Sample
SS=Σx²-(Σx)²/N  Computation
SS=Σ( x-μ)²  Definition
Sum of Squared Deviation from Mean
Variance (σ²) is the Mean of Squared Deviations=MS22

23. 23
Practical Implication for Test
Construction
Variance and Covariance measure the quality of each
item in a test.
Reliability and validity measure the quality of the
entire test.
 σ²=SS/N  used for one set of data
Variance is the degree of variability
of scores from mean.
Correlation is based on a statistic called Covariance (Cov xy
or S xy) ….. r=sp/√ssx.ssy
 COVxy=SP/N-1  used for 2 sets of data
Covariance is a number that reflects the degree to
which 2 variables vary together.

24. 24
Variance
 X σ² = ss/N Pop
1 s² = ss/n-1 or ss/df Sample
2
4
5
SS=Σx²-(Σx)²/N
SS=Σ( x-μ)²
Sum of Squared Deviation from Mean

25. 25
Covariance
 Correlation is based on a statistic called
Covariance (Covxy or Sxy) …..
COVxy=SP/N-1
Correlation-- r=sp/√ssx.ssy
 Covariance is a number that reflects the
degree to which 2 variables vary
together.
 Original Data
X Y
1 3
2 6
4 4
5 7

26. 26
Covariance
 Correlation is based on a statistic called
Covariance (Covxy or Sxy) …..
COVxy=SP/N-1
Correlation-- r=sp/√ssx.ssy
 Covariance is a number that reflects the
degree to which 2 variables vary
together.
 Original Data
X Y
8 1
1 0
3 6
0 1

27. 
27
Covariance

28. 28
Descriptive Statistics for
Nondichotomous Variables

29. 29
Descriptive Statistics for
Dichotomous Data

30. 30
Descriptive Statistics for
Dichotomous Data
Item Variance & Covariance

31. FACTORS THAT AFFECT
VARIABILITY
 1. Extreme Scores i.e. 1, 3, 8, 11, 1,000,000.00 . We can’t use
the Range in this situation but we can use the other measures of
variability.
 2. Sample Size If we increase the sample size will change the
Range therefore we can’t use the Range in this situation but we can
use the other measures of variability.
 3. Stability Under Sampling (see next slide) p.130 The
S and S² for all samples should be the same because they come from
same population (all slices of a pizza should taste the same).
 4. Open-Ended Distribution When we don’t have
highest score and lowest score in a distribution
31

32. 32