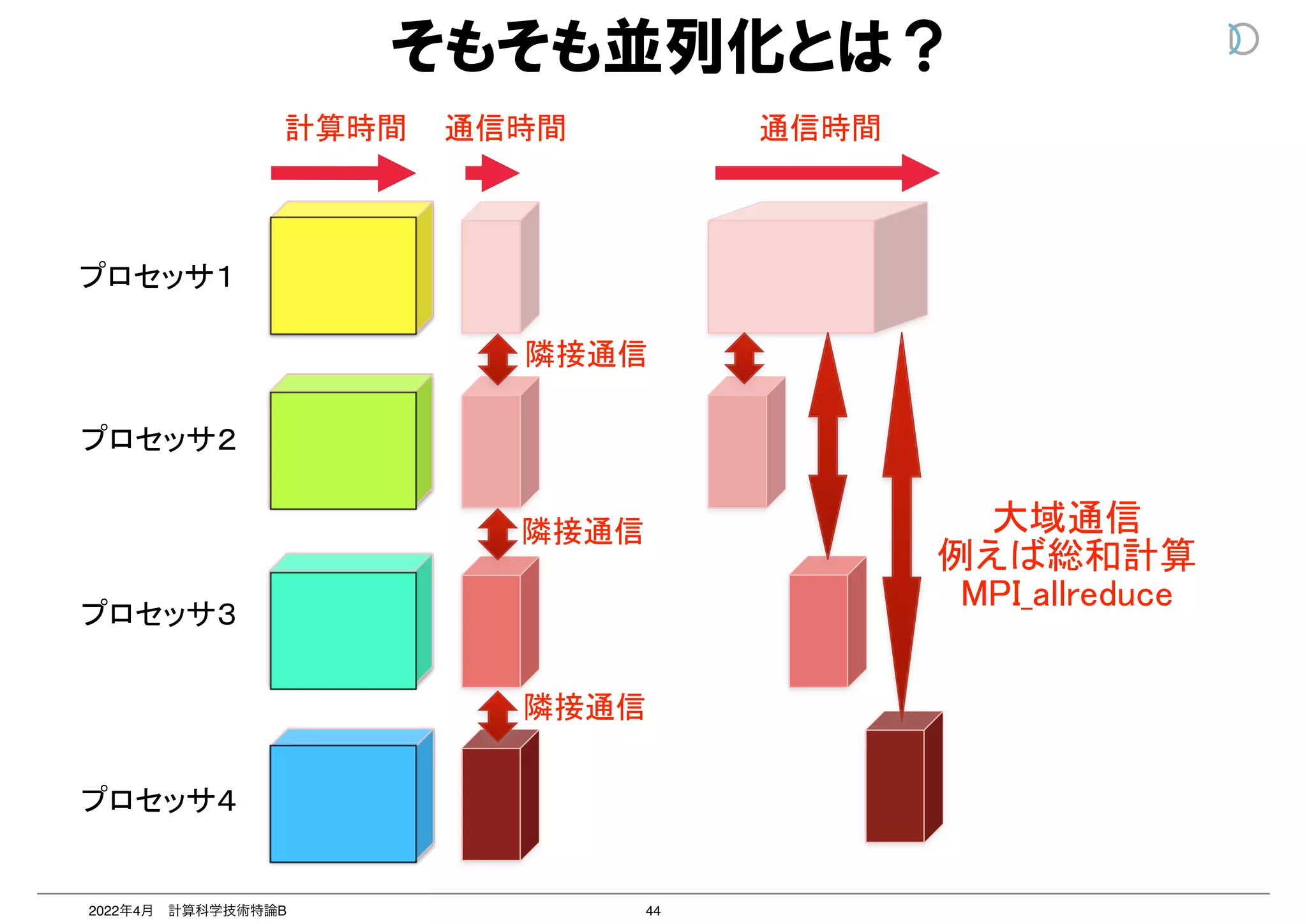
第1回で述べたようなハードウェアの状況のもと、スーパーコンピュータ上で実行されるアプリケーションは、高度な並列化と個々のノード内のハードウェア性能を使い切るための性能最適化、いわゆるチューニングを実施しない限り、ハードウェアのパフォーマンスを十分に活用することはできない。
つまり「並列を意識したプログラミング」と「単体CPU実行性能を意識したプログラミング」という2つのポイントは、何万ものプロセッサを搭載し、さまざまな新機能・強化された機能を備えた現在のスーパーコンピュータを使用するユーザー、研究者、およびプログラマーにとって不可欠のテクニックである。
第2回は、2つのポイントのうち「並列を意識したプログラミング」いわゆる「高並列性能最適化」について抗議する。








![12
2022年4月 計算科学技術特論B
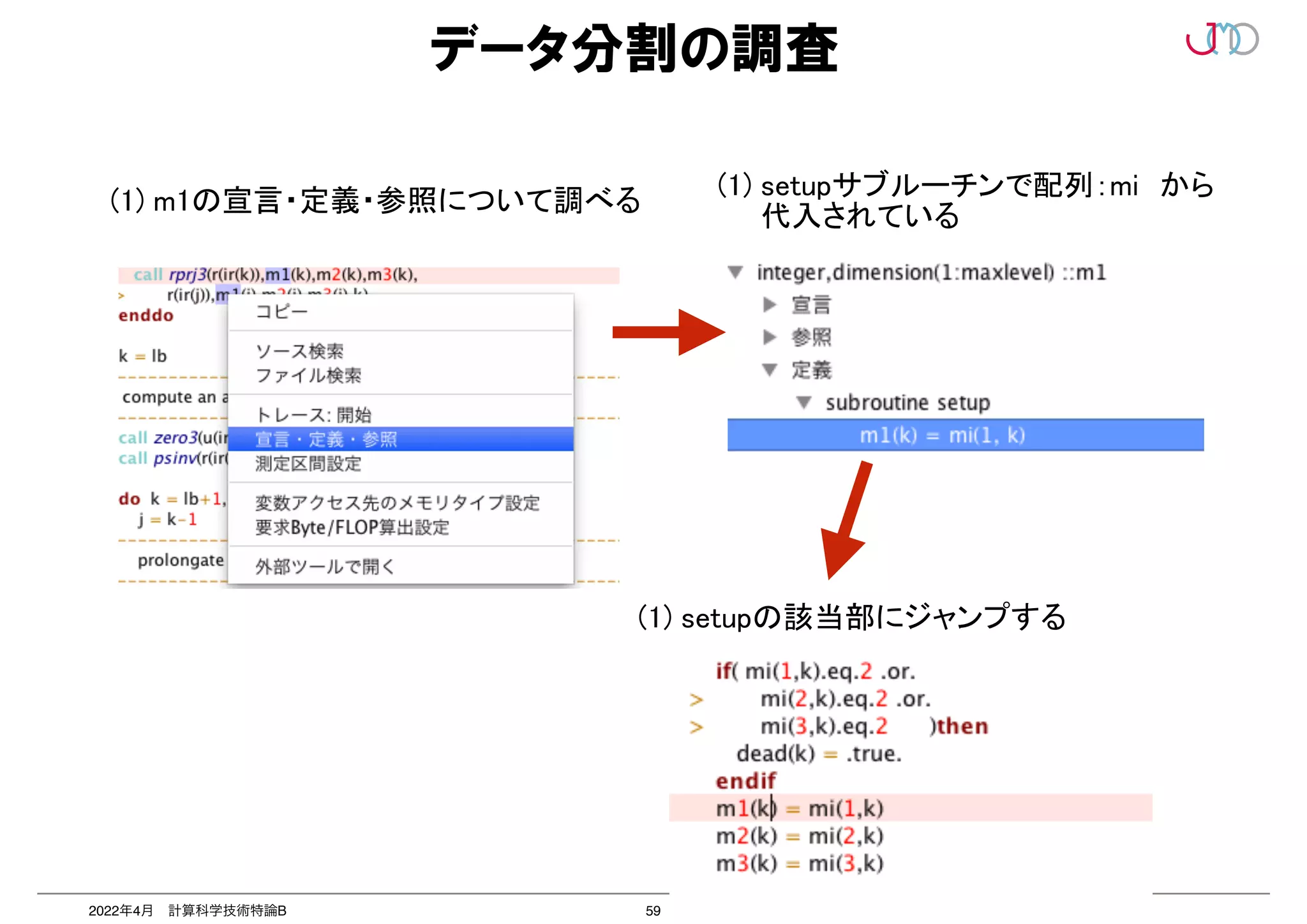
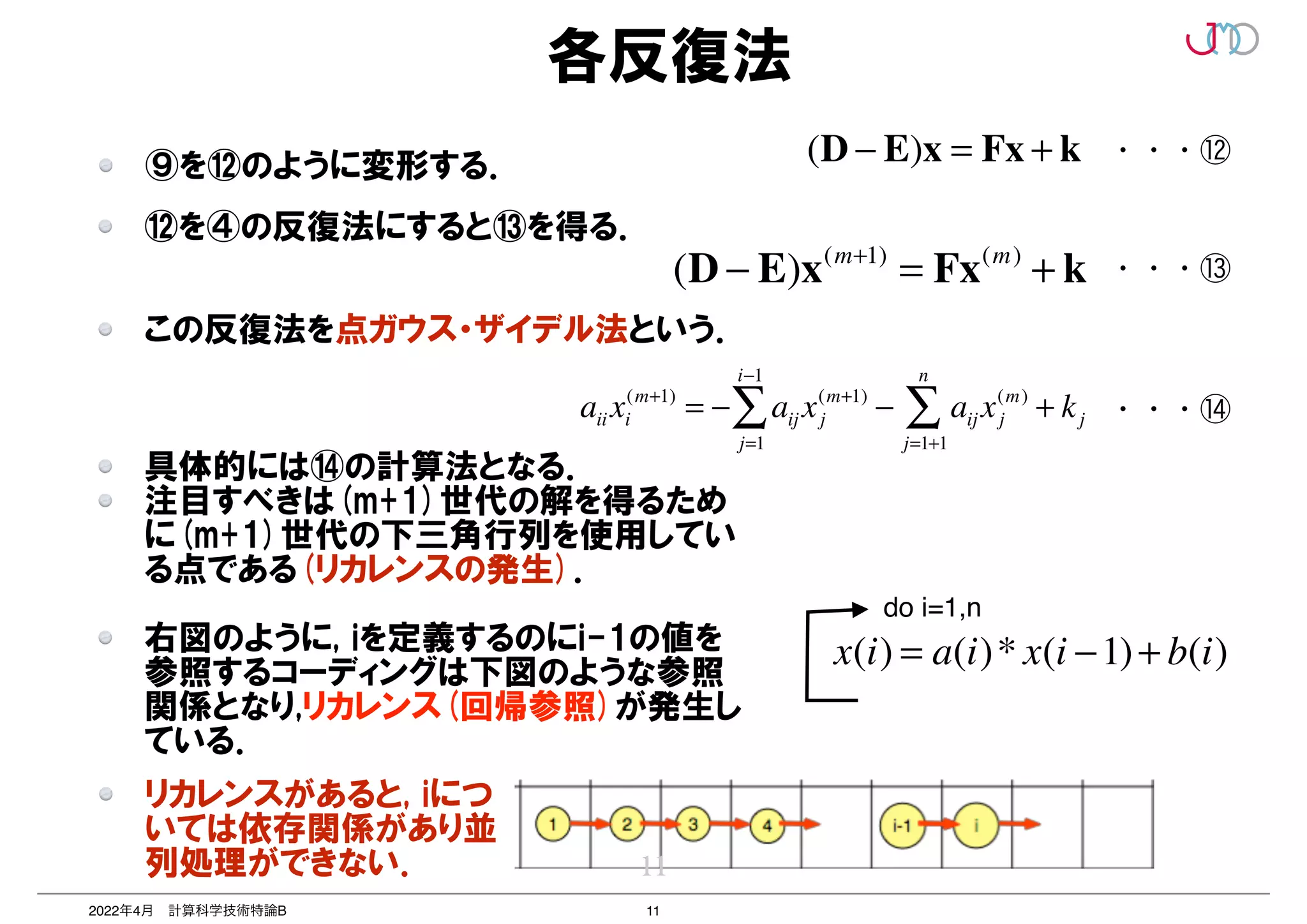
リカレンスがあると...
大昔の計算機
演算3
演算器
演算器に逐次に入力し逐次実行
演算2
演算1
性能向上
(1)そのまま実行すると6clock
演算1 演算2
(2)演算を3つのス
テージに分割する
演算i
(3)並列に計算できるようスケジューリング
(4)2個の演算資源を使い並列に実行
(5)4clockで実行可
(6)演算を細かく分割し複数の演算資源を
並列に動作し性能アップ
演算[i+1]
演算[i]
処理のリカレンスをなくすチューニングは
現代のコンピュータを使う上で必須事項!](https://image.slidesharecdn.com/2022-220411235350/75/2-B-2022-12-2048.jpg)















![35
2022年4月 計算科学技術特論B
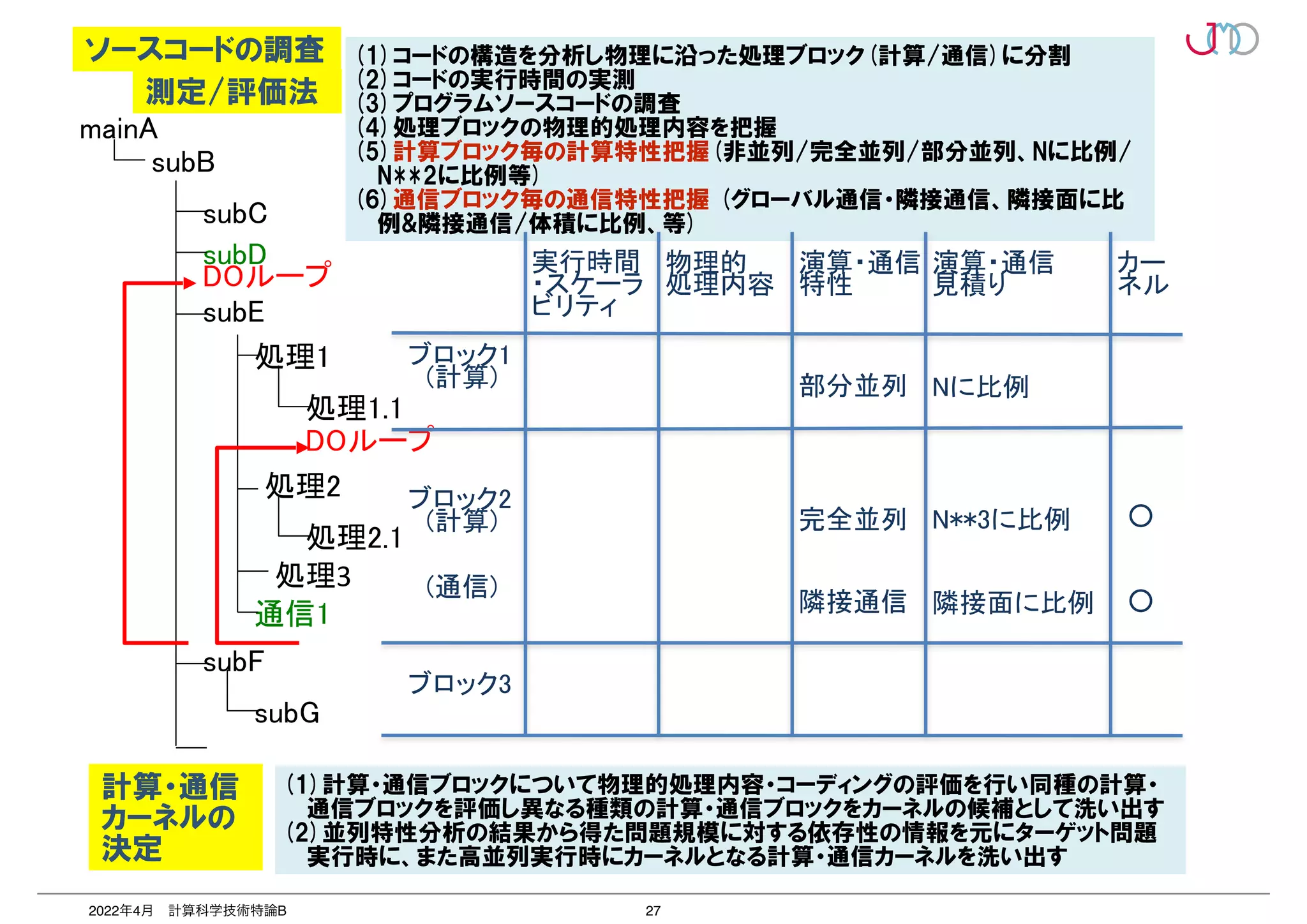
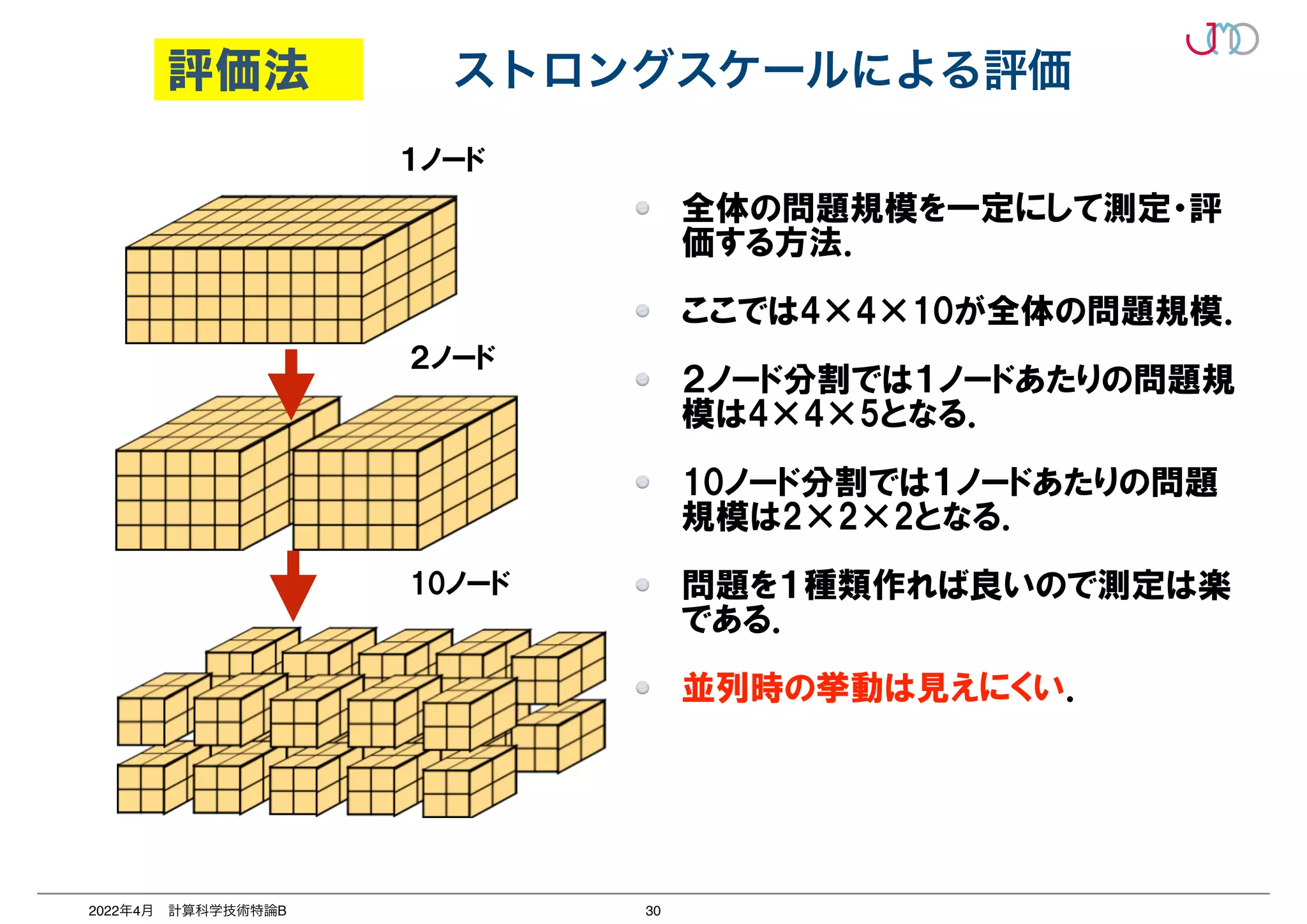
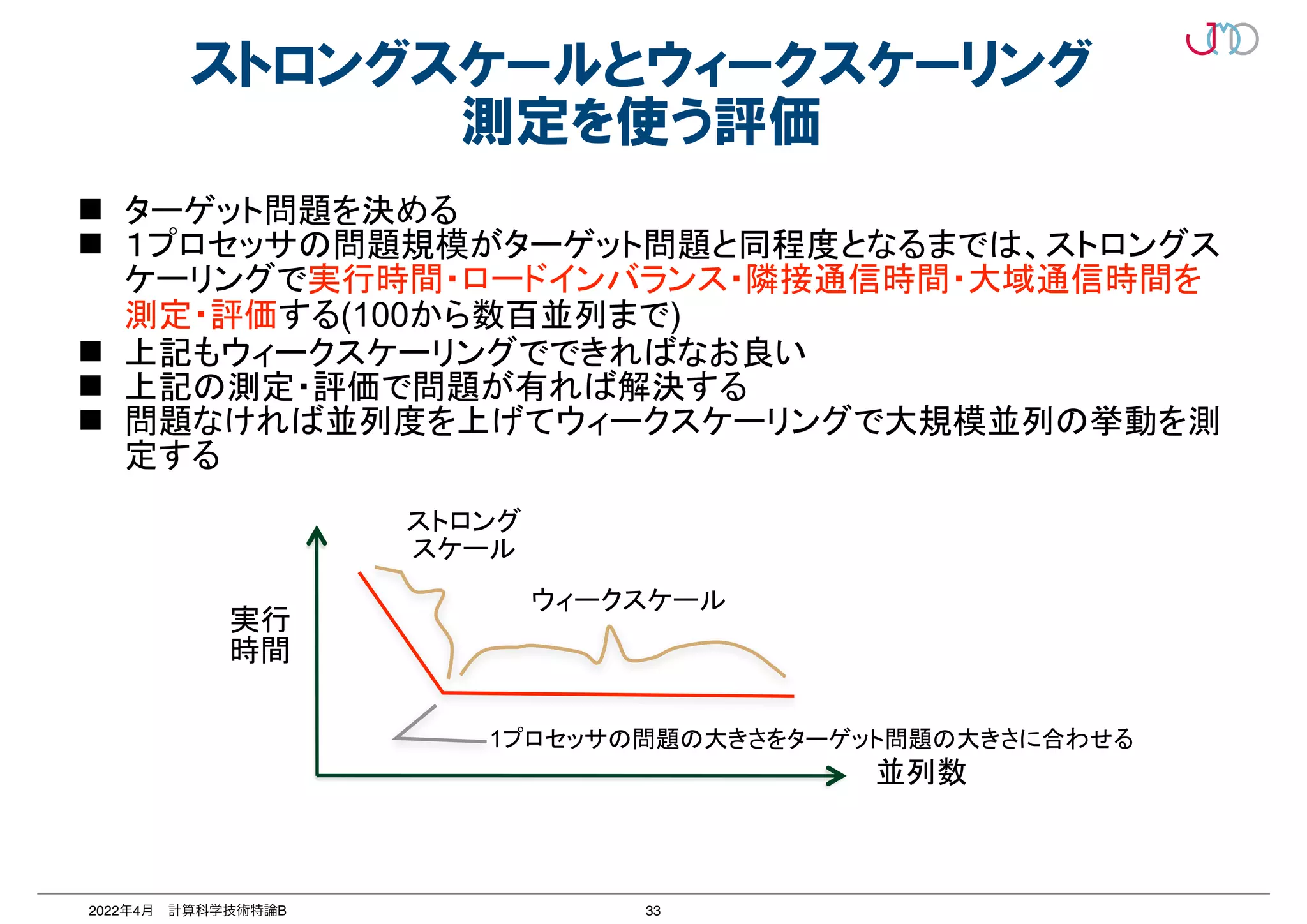
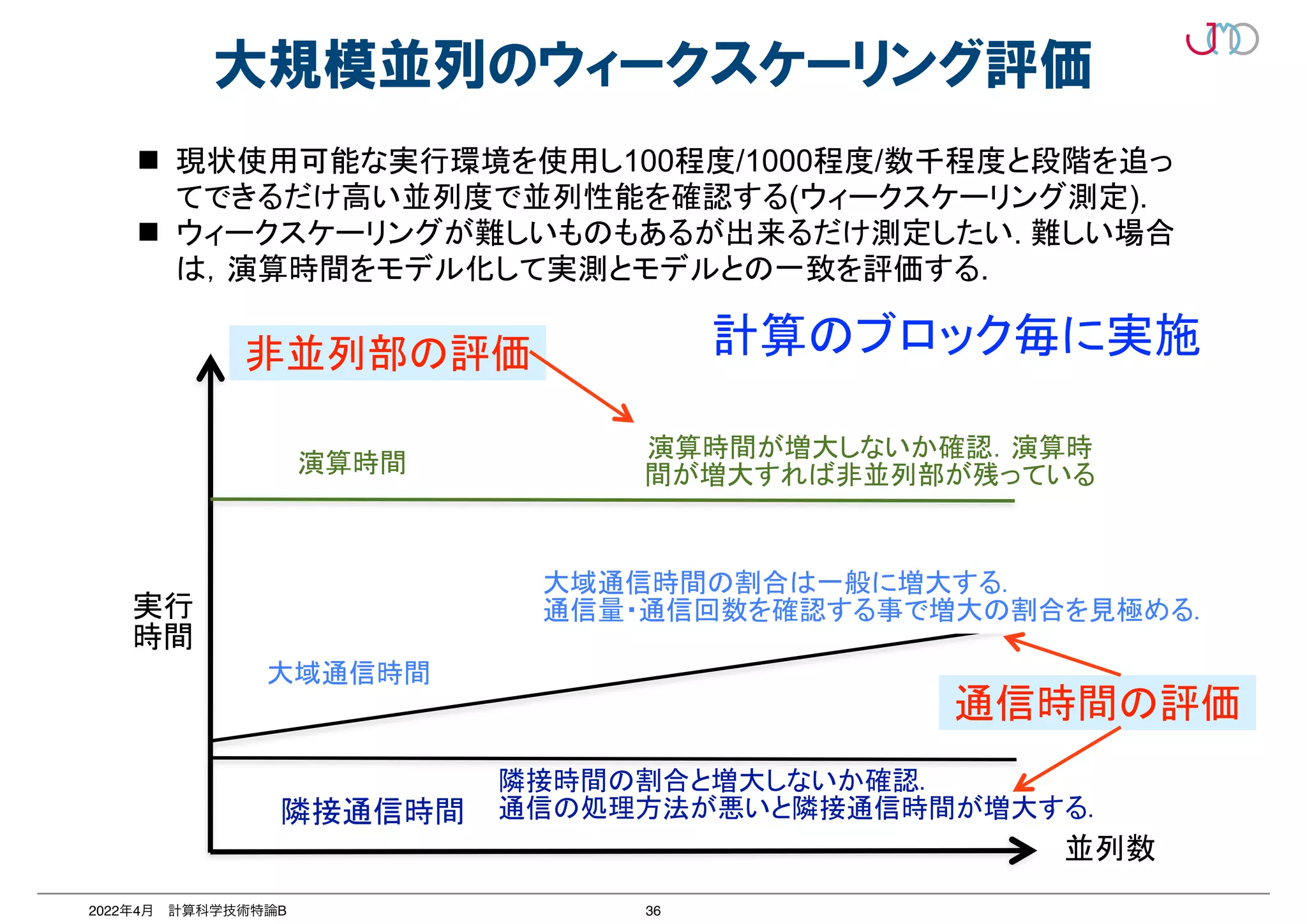
大規模並列のウィークスケーリング評価
場合が出てくる。これが、アプリケーションとハードウェアの並列度のミスマッ
アプリケーションの並列度の限界に近づいてくると、演算時間が著しく小さくな
し通信時間の割合が増大する状態となり、並列効率の悪化を招く。
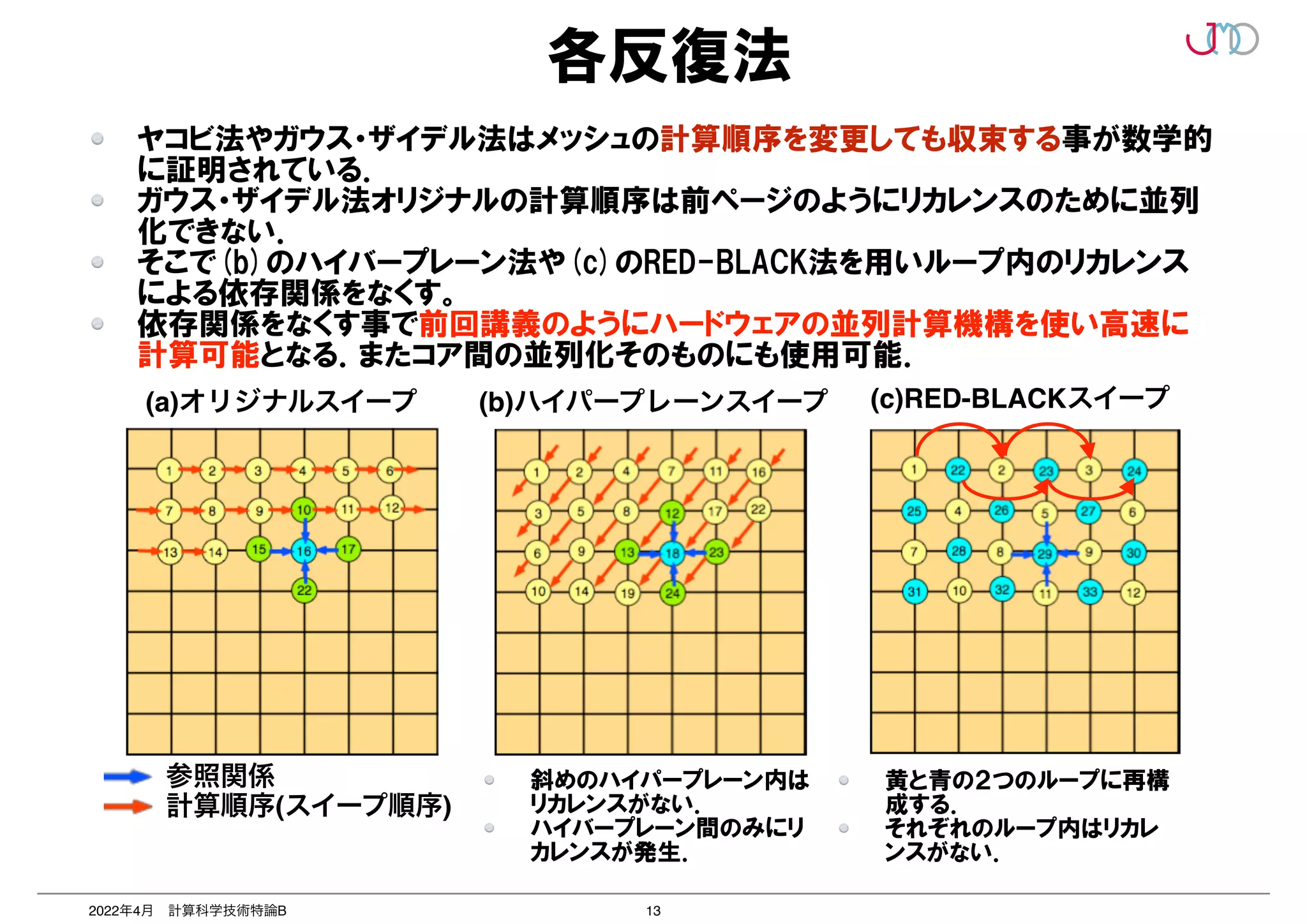
2 点目は、非並列部の残存である。本節の冒頭に述べたように、演算部分に非
残っているとアムダールの法則により、並列性能の悪化を招く。ここで、あるア
ションの逐次実行時の実行時間を Ts であるとし、そのアプリケーションの並列
であるとすると、アプリケーションの非並列化率は 1 − α となる。このアプリケ
を並列度 n で実行すると、n 並列での実行時間 Tn は、Tn = Ts(α
n + (1 − α)
る。仮に n = 10000 の時に並列化効率 50%を達成するための α を求めると、並
は 99.99%を要求されることになる。非並列部の残存を発見しやすいのは、前述
ウィークスケーリング測定による、演算部の実行時間の増大である。
3 点目は、大域通信における大きな通信サイズ、通信回数の発生である。通信
に大域通信は、並列性能に大きな影響を与える。n ノード間で m[Byte] の allr
を実施する例を考える。2 分木のアルゴリズムにより allreduce 通信を実施し通
Pt[B/sec] と仮定すると、全ノードが通信を終わり m[Byte] の総和量を取得する
信時間 T は、T = m×log 2n
Pt
で計算される。大域通信と隣接通信と比較するため
ドが隣のランクに m[Byte] の隣接通信を実施する例を考える。通信性能を上記の
m
度しか使えない、という
列度のミスマッチである。
著しく小さくなるのに対
。
、演算部分に非並列部が
ここで、あるアプリケー
ーションの並列化率を α
。このアプリケーション
(α
n + (1 − α)) で表され
を求めると、並列化率 α
すいのは、前述した通り
る。
生である。通信時間、特
[Byte] の allreduce 通信
通信を実施し通信性能が
和量を取得するための通
比較するために、n ノー
ョンの並列化の限界から、数千の並列度しか使えない、という
アプリケーションとハードウェアの並列度のミスマッチである。
の限界に近づいてくると、演算時間が著しく小さくなるのに対
る状態となり、並列効率の悪化を招く。
存である。本節の冒頭に述べたように、演算部分に非並列部が
法則により、並列性能の悪化を招く。ここで、あるアプリケー
時間を Ts であるとし、そのアプリケーションの並列化率を α
ーションの非並列化率は 1 − α となる。このアプリケーション
n 並列での実行時間 Tn は、Tn = Ts(α
n + (1 − α)) で表され
並列化効率 50%を達成するための α を求めると、並列化率 α
とになる。非並列部の残存を発見しやすいのは、前述した通り
による、演算部の実行時間の増大である。
ける大きな通信サイズ、通信回数の発生である。通信時間、特
大きな影響を与える。n ノード間で m[Byte] の allreduce 通信
分木のアルゴリズムにより allreduce 通信を実施し通信性能が
全ノードが通信を終わり m[Byte] の総和量を取得するための通
で計算される。大域通信と隣接通信と比較するために、n ノー
プリケーションの並列化の限界から、数千の並列度しか使えない、という
。これが、アプリケーションとハードウェアの並列度のミスマッチである。
ンの並列度の限界に近づいてくると、演算時間が著しく小さくなるのに対
合が増大する状態となり、並列効率の悪化を招く。
列部の残存である。本節の冒頭に述べたように、演算部分に非並列部が
ムダールの法則により、並列性能の悪化を招く。ここで、あるアプリケー
行時の実行時間を Ts であるとし、そのアプリケーションの並列化率を α
、アプリケーションの非並列化率は 1 − α となる。このアプリケーション
行すると、n 並列での実行時間 Tn は、Tn = Ts(α
n + (1 − α)) で表され
000 の時に並列化効率 50%を達成するための α を求めると、並列化率 α
されることになる。非並列部の残存を発見しやすいのは、前述した通り
リング測定による、演算部の実行時間の増大である。
通信における大きな通信サイズ、通信回数の発生である。通信時間、特
並列性能に大きな影響を与える。n ノード間で m[Byte] の allreduce 通信
考える。2 分木のアルゴリズムにより allreduce 通信を実施し通信性能が
すると、全ノードが通信を終わり m[Byte] の総和量を取得するための通
ケーションの並列化の限界から、数千の並列度しか使えない、という
れが、アプリケーションとハードウェアの並列度のミスマッチである。
並列度の限界に近づいてくると、演算時間が著しく小さくなるのに対
が増大する状態となり、並列効率の悪化を招く。
部の残存である。本節の冒頭に述べたように、演算部分に非並列部が
ダールの法則により、並列性能の悪化を招く。ここで、あるアプリケー
時の実行時間を Ts であるとし、そのアプリケーションの並列化率を α
アプリケーションの非並列化率は 1 − α となる。このアプリケーション
すると、n 並列での実行時間 Tn は、Tn = Ts(α
n + (1 − α)) で表され
0 の時に並列化効率 50%を達成するための α を求めると、並列化率 α
れることになる。非並列部の残存を発見しやすいのは、前述した通り
ング測定による、演算部の実行時間の増大である。
信における大きな通信サイズ、通信回数の発生である。通信時間、特
列性能に大きな影響を与える。n ノード間で m[Byte] の allreduce 通信
える。2 分木のアルゴリズムにより allreduce 通信を実施し通信性能が
ると、全ノードが通信を終わり m[Byte] の総和量を取得するための通
非並列部の評価
Tn = Ts
α
n
+Ts (1−α)
T2n = 2Ts
α
2n
+ 2Ts (1−α) = Ts
α
n
+ 2Ts (1−α)
並列度を上げると,ここが
どんどん大きくなる](https://image.slidesharecdn.com/2022-220411235350/75/2-B-2022-35-2048.jpg)




![42
2022年4月 計算科学技術特論B
非並列部の残存
第一原理アプリケーションの処理ブロック:ノンローカル項の計算部分を例に示す.
低並列でストロングスケールで測定.
すでにこの並列度でスケールしていない.原因は次ページに示す.
!
BLAS Level3 ( 2)
(
!
BLAS Level3 ( 2)
(
0
2
4
6
8
10
12
14
16
[s]](https://image.slidesharecdn.com/2022-220411235350/75/2-B-2022-42-2048.jpg)