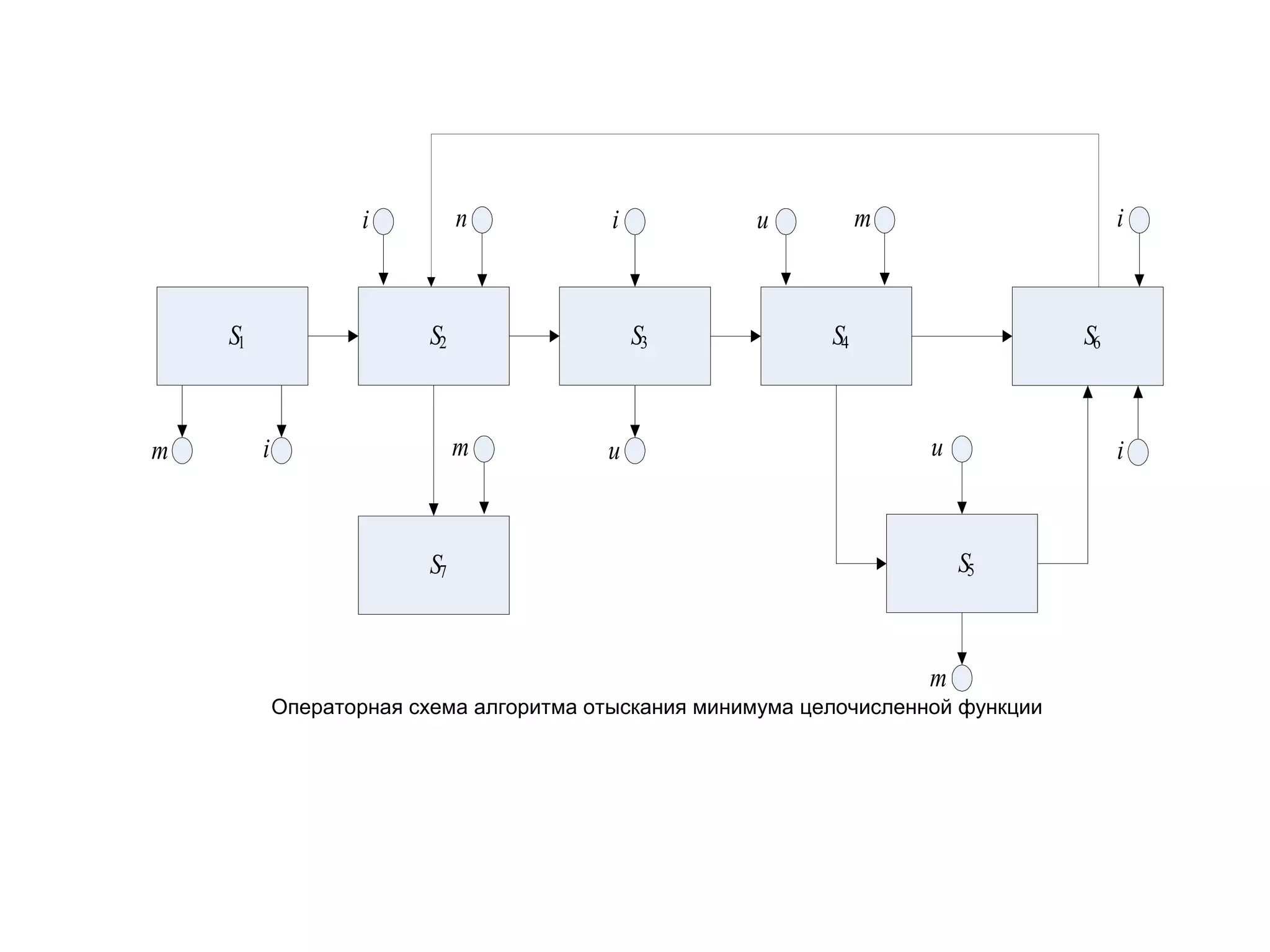
Документ описывает методы доказательства корректности алгоритмов через операторные схемы, рассматривая их структуру, свойства и спецификации. Основное внимание уделяется ряду теорем, обеспечивающих корректность выполнения операторов и установление связи между состояниями переменных и предикатами. Также обсуждаются проблемы оценки трудоемкости и экономии памяти в алгоритмах.