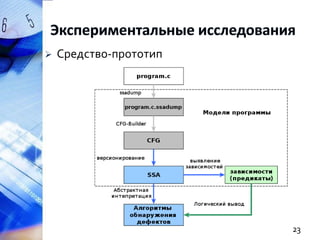
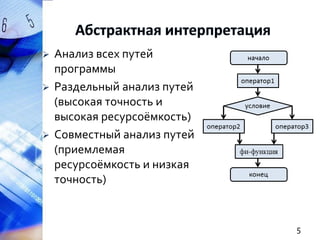
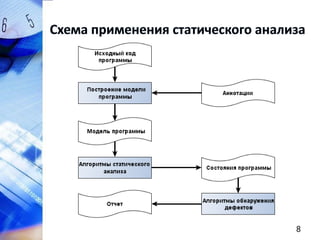
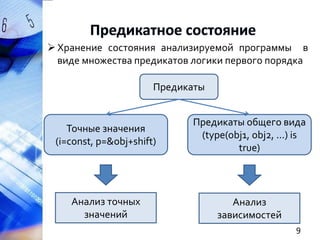
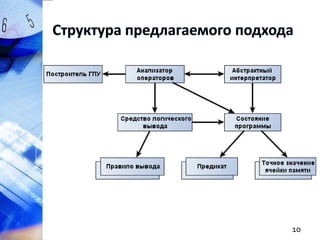
Документ описывает методы статического анализа программ на C/C++, сосредоточенные на обнаружении дефектов, связанных с указателями, и использовании логического вывода. Рассматриваются такие аспекты, как полнота и точность анализа, извлечение предикатов, и предложены алгоритмы и правила для улучшения качества статического анализа. В заключение упоминается реализация предложенных методов в исследовательском прототипе на базе анализатора aegis и SMT-решателя Microsoft Z3.

1. Обнаружение дефектов работы с
указателями в программах на языках
C/C++ с использованием статического
анализа и логического вывода
Татьяна Верт, Татьяна Крикун (Санкт-Петербургский
государственный политехнический университет)
Михаил Глухих (Технический университет Клаусталя)

2. 

Программное обеспечение содержит ошибки
Функциональные ошибки
o Программа не соответствует спецификации

Нефункциональные ошибки (программные
дефекты)
o Использование неинициализированных
переменных
o Некорректное использование указателей
o Выходы за границы массивов
2

3. 

Полнота – доля истинных обнаруженных дефектов
среди всех дефектов, имеющихся в программе
Точность – доля истинных обнаруженных дефектов
среди всех обнаруженных дефектов
Два из Трех
Высокая
полнота
Низкая
ресурсоемкость
Высокая
точность
3

4. 4

5. 


Анализ всех путей
программы
Раздельный анализ путей
(высокая точность и
высокая ресурсоёмкость)
Совместный анализ путей
(приемлемая
ресурсоёмкость и низкая
точность)
5

6. 


Зависимость – произвольная связь между
значениями двух и более переменных
программы
Математически, зависимость может быть
представлена в виде предиката
Анализ
зависимостей
позволяет
компенсировать погрешность, вызванную
слиянием путей в ходе статического анализа
6

7. 
Использование средств логического вывода
для доказательства различных утверждений
в ходе статического анализа, в частности,
утверждений о наличии либо отсутствии
дефектов
в
отдельных
операторах
программы
7

8. 8

9.  Хранение состояния анализируемой программы в
виде множества предикатов логики первого порядка
Предикаты
Точные значения
(i=const, p=&obj+shift)
Предикаты общего вида
(type(obj1, obj2, ...) is
true)
Анализ точных
значений
Анализ
зависимостей
9

10. 10

11. 


Извлечение предикатов при интерпретации
операторов
Типы предикатов:
– арифметические (A=B+C, A=B*C, A=B%C, и т. д.)
– логические (A=￢B, A=B∨D, A=B∧D, A→B)
– сравнения (A>B, A<B, A≥B, A≤B, A≠B)
– работа с указателями(A=&B+C, A=*B)
– обращение к составному объекту(A=B[C], A=B.C)
– размер объекта(A = sizeof B, A ≤ sizeof B)
–…
Представление: 𝑝(𝑣1 , 𝑣2 , … , 𝑣 𝑛 ), где 𝑝 функциональный символ, 𝑣 𝑖 , 𝑖 = 1 … 𝑛 – предикатные
переменные
11

12. 

Переменными предикатов являются другие
предикаты
Примеры:
– 𝑜𝑛𝑒𝑜𝑓 𝑝1 , 𝑝2 – истинен хотя бы один из двух
предикатов 𝑝1 , 𝑝2
– 𝑜𝑝𝑝𝑜𝑠(𝑝) – предикат 𝑝 ложен
– 𝑒𝑞𝑢𝑖𝑣 𝑝1 , 𝑝2 – предикаты 𝑝1 и 𝑝2 одновременно
истинны или одновременно ложны
 Сложные предикаты также могут быть описаны в
терминах логики первого порядка
12

13. 
Представление переменных на основе статического
однократного присваивания (SSA):
– Каждой переменной значение присваивается
только один раз;
– В случае присвоения нескольких значений
используется версионирование переменных.
x = a + b;
x.1 = a.1 + b.1;
y = x * x;
y.1 = x.1 * x.1;
x = c + d;
x.2 = c.1 + d.1;
𝑠𝑢𝑚 𝑥1 , 𝑎1 , 𝑏1
mult 𝑦1 , 𝑥1 , 𝑥1
s𝑢𝑚 𝑥2 , 𝑐1 , 𝑑1
13

14. 
Выявление зависимостей при интерпретации:
– операторов определения переменной
– операторов прямого присваивания lvar=…
•
•
•
•
•
Присваивания lvar=rvar
Присваивания lvar=binary(arg1, arg2)
Присваивания lvar=unary(rvar)
Присваивания адреса lvar=&rvar
Присваивания
через
косвенную
lvar=*rvar
адресацию
– операторов косвенного присваивания *lvar=rvalue
– операторов ветвления if (cond)
– операторов выделения/освобождения памяти
14

15. 


Объединение состояний программы в точках слияния
путей
Любое условие сохраняется на выходе фи-функции
только в том случае, если оно имелось на всех её
входах
Если
некоторой
переменной
программы
𝑣 соответствуют разные предикатные переменные
𝑣1 и 𝑣2 во входных состояниях, то для неё создается
новая предикатная переменная 𝑣3 , при этом в
выходное
состояние
добавляется
предикат
𝑜𝑛𝑒𝑜𝑓(𝑒𝑞𝑢𝑎𝑙𝑠(𝑣3 , 𝑣1 ), 𝑒𝑞𝑢𝑎𝑙𝑠(𝑣3 , 𝑣2 ))
15

16. 
Если объект имеет разные версии в разных ветвях
условного оператора, предикат, описывающий его
значение, следует привязать к условию оператора if

Пример:
if (size > 0)
q = malloc(size);
else
q = 0;
Предикатное состояние
Истинная ветвь
Ложная ветвь
𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑠𝑖𝑧𝑒1 , 0
𝑙𝑒𝑠𝑠_𝑒𝑞𝑢𝑎𝑙𝑠 𝑠𝑖𝑧𝑒1 , 0
𝑠𝑖𝑧𝑒𝑜𝑓 𝑑𝑦𝑛, 𝑠𝑖𝑧𝑒1
𝑒𝑞𝑢𝑎𝑙𝑠 𝑞2 , 0
𝑝𝑡𝑟 𝑑𝑦𝑛, 𝑞1 , 0
Выходное состояние
𝑜𝑛𝑒𝑜𝑓(𝑒𝑞𝑢𝑎𝑙𝑠(𝑞3 , 𝑞1 ), 𝑒𝑞𝑢𝑎𝑙𝑠(𝑞3 , 𝑞2 ))
𝑒𝑞𝑢𝑖𝑣(𝑙𝑒𝑠𝑠_𝑒𝑞𝑢𝑎𝑙𝑠 𝑠𝑖𝑧𝑒1 , 0 , 𝑒𝑞𝑢𝑎𝑙𝑠 𝑞3 , 0 )
16

17. 
Обнаружение дефектов при анализе операции
разадресации *ptr и операции обращения по индексу
ptr[i]
• Некорректное использование указателей:
int* ptr = 0;
if (array[0]>0)
ptr=array;
int val=*ptr; //разадресация нулевого указателя
• Выход за границу объекта
int
int
i =
a =
a, i;
array[9];
10;
array[i]; //выход за границу массива
17

18. 
Корректность указателя
p = (void*)(&t)+s; v = sizeof(t);
𝑝𝑡𝑟 𝑡, 𝑝, 𝑠 , 𝑠𝑖𝑧𝑒𝑜𝑓 𝑡, 𝑣 , 𝑔𝑟𝑒𝑎𝑡𝑒𝑟_𝑒𝑞𝑢𝑎𝑙𝑠(𝑠, 0), 𝑙𝑒𝑠𝑠(𝑠, 𝑣)
𝑐𝑜𝑟𝑟𝑒𝑐𝑡_𝑝𝑡𝑟(𝑝)
 Разадресация указателя v = *p;
1) Указатель на простую переменную
p = (void*)(&t);
𝑝𝑡𝑟 𝑡,𝑝,0 ,𝑑𝑒𝑟𝑒𝑓(𝑝,𝑣)
𝑒𝑞𝑢𝑎𝑙𝑠(𝑡,𝑣)
2) Указатель на элемент составного объекта
p = (void*)(&a)+s; t = *(&a +s);
𝑝𝑡𝑟 𝑎, 𝑝, 𝑠 , 𝑎𝑟𝑟 𝑎, 𝑡, 𝑠 , 𝑑𝑒𝑟𝑒𝑓(𝑝, 𝑣)
𝑒𝑞𝑢𝑎𝑙𝑠(𝑡, 𝑣)
18

19. 
Сложение указателя с целочисленной
константой
p = (void*)(&a)+s; t=s+b; q = p+b;
𝑝𝑡𝑟 𝑎, 𝑝, 𝑠 , 𝑠𝑢𝑚 𝑡, 𝑠, 𝑏 , 𝑠𝑢𝑚(𝑞, 𝑝, 𝑏)
𝑝𝑡𝑟(𝑎, 𝑞, 𝑡)
19

20. 

Присутствие дефекта – доказательство
разрешимости предикатов:
– нулевой указатель:𝑒𝑞𝑢𝑎𝑙𝑠(𝑝𝑡𝑟, 0)
– некорректный
указатель: 𝑜𝑝𝑝𝑜𝑠(𝑐𝑜𝑟𝑟𝑒𝑐𝑡_𝑝𝑡𝑟(𝑝𝑡𝑟))
Отсутствие дефекта – неразрешимость
предикатов
20

21. …
int x,b;
std::cin >> x;
int arr[5]={0,1,2,3,4};
if (x>0){
b = arr[x];
}
…
Предикаты
sizeof(arr, 20),
equals(arr[0]_0, 0),
equals(arr[1]_0, 1),
equals(arr[2]_0, 2),
equals(arr[3]_0, 3),
equals(arr[4]_0, 4),
greater(x_0, 0),
ptr(arr, tmp1_0, 0)),
mult(tmp2_0, x_0, 4),
sum(tmp3_0, tmp1_0,tmp2_0)
ptr(arr, tmp3, tmp2), sizeof(arr, 20), or(less(tmp2, 0),
greater_equals(tmp2, 20)) = > oppos(correct_ptr(tmp3))
21

22. 
Доказатели теорем
– HOL Theorem Prover

Языки логического программирования
– Bprolog

SMT-решатели
– Z3
22

23. 
Средство-прототип
23

24. Пример Истинных
дефектов
1
2
3
4
5
6
7
8
1
2
1
2
0
2
0
2
Полнота
Точность
Среднее время
Разработанная
Aegis
система
(Digitek Labs)
дефектов ложных дефектов ложных
найдено дефектов найдено дефектов
найдено
найдено
1
0
1
0
2
0
0
0
1
0
1
0
2
0
3
1
0
0
1
1
2
0
3
1
0
0
2
2
1
0
1
0
…
95%
75%
95%
68%
53 сек.
5 сек.
FlexeLint
(Gimpel Software)
дефектов ложных
найдено дефектов
найдено
1
0
0
0
0
0
3
1
1
1
1
1
1
1
1
0
45%
60%
4 сек.
24

25. 



Применение алгоритмов сборки мусора
Применение
алгоритмов
упрощения
состояния программы
Разработка
механизма
выделения
инвариантов цикла
Обнаружение более широкого класса
программных дефектов
25

26. 




Рассмотрен подход к статическому анализу с
использованием средств логического вывода.
Приведены правила извлечения предикатов из
различных операторов анализируемой программы.
Разработаны логические правила вывода для анализа
указателей и обнаружения дефектов работы с
указателями.
Приведённые алгоритмы анализа реализованы в
исследовательском прототипе на базе анализатора
Aegis и SMT-решателя Microsoft Z3.
Показано значительное повышение точности по
сравнению с базовым анализатором.
26

27. 27

28. 



Предикат – логическое утверждение, которое
может быть как истинно, так и ложно, зависящее от
ряда предикатных объектов.
Зависимость – связь между значениями двух и
более программных объектов.
Фи-функция – точка слияния двух и более потоков
выполнения программы.
Абстрактная интерпретация – общая теория,
которая задает способ аппроксимации семантики
динамических дискретных систем, в том числе компьютерных программ.
28

29. 

Логика первого порядка (исчисление предикатов) –
формальное исчисление, допускающее высказывания
относительно переменных, фиксированных функций и
предикатов.
Граф потока управления – модель программы,
представляющая в виде ориентированного графа
потоки управления программы. Дуги графа
отображают возможный ход вычислительного
процесса, вершины графа соответствуют инструкциям
программы.
29