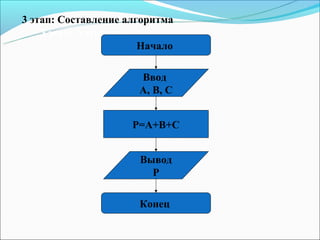
Документ содержит информацию о Черняковой Ганне Валентиновне, в том числе ее данные о рождении, образовании и профессиональной деятельности в области математики и информатики. Также представлены ее достижения, педагогический стаж и примеры алгоритмов, таких как алгоритм Евклида и решето Эратосфена, а также задачи, связанные с целочисленной оптимизацией. Включены описания методов и примеры использования, что подчеркивает ее опыт в обучении и разработке образовательных материалов.

1. Чернякова
Ганна
Валентинівна

2.  Дата народження: 10 грудня 1950 року.
 Кредо: “ Понимать , что справедливо ,чувствовать.”
 Освіта: вища. Дніпропетровський державний університет. 1973 рік
випуску.
 Спеціальність: математик,математик-обчислювач.
 Посада:вчитель інформатики, вища категорія, старший вчитель.
 Педагогічний стаж:20 років.
 Нагороди:знак -” Відмінник освіти України ”,ПОЧЕСНА ГРАМОТА-
управління освіти та науки Дніпропетровської міської ради 2002рік,
ПОДЯКА - Самарська района у м. Дніпропетровську Рада-№61 від
26.06.2006р.,ГРАМОТА-головне управління освіти і науки
Дніпропетровської обласної державної адміністрації-жовтень 2008року.
 Сертифікат №38/Д4РТ . Курс-Intel навчання для майбутнбого
 Кваліфікаційне посвідчення: №2502 від 21.06.2003 р.

3. Тема самоосвіти:”Розвиток та формування логічного мислення
учнів, розкриття творчого потенціалу учнів.”
Використання сучасних методик та технологій навчання:метод
проектів, інтерактивні методи,
диференційовано-індивідуальну
систему завдань, пошукові.
Результативність роботи: Хащин Андрій - 2008 р. переможець в
олімпіаді з програмування.
Форми узагальнення досвіду роботи:розробки практичних робіт
для 10класів, розробки лекцій та
практичних робіт для 11 класів

5. Классификация алгоритмов по
структуре:
Линейный (следование)
Разветвленный (ветвление, выбор,
альтернатива)
Циклический (повтор)
Вспомогательный
Комбинированный

6. Алгоритм – это строго
определенная последовательность
действий при решении задачи.
Алгоритм содержит несколько
шагов.
Шаг алгоритма – это каждое
отдельное действие алгоритма.

7. Исполнитель – это объект, умеющий
выполнять определенный набор
действий. Исполнителем может быть
человек, робот, животное, компьютер.
Система команд исполнителя (СКИ) –
это все команды, которые исполнитель
умеет выполнять.
Среда исполнителя – обстановка, в
которой функционирует исполнитель.

8. Задание: Назови исполнителей
следующих видов работы:
Уборка мусора во дворе
Обучение детей в школе
Вождение автомобиля
Ответ у доски
Приготовление пищи
Печатание документа на принтере

9. Результативность – получение Свойства алгоритма
Результативность
результата за конечное
количество шагов
Дискретность (прерывность,
Дискретность
раздельность) – разбиение
алгоритма на шаги
Детерминированность
АЛГОРИТМ Детерминированность
(определенность, точность) –
каждое действие должно строго и
недвусмысленно определено
Конечность – каждое действие в
отдельности и алгоритм в целом
Конечность
Массовость – использование должны иметь возможность
алгоритма для решения однотипных завершения
Массовость
задач

10. Классификация алгоритмов по
форме представления:
Словесные
Табличные
Графические (блок-схемы)
Программные

11. Таблица основных условных обозначений
в блок-схемах
Условное Назначение блока
обозначение
Начало или конец алгоритма
Ввод или вывод данных.
Внутри блока перечисляются
данные через запятую.
Процесс.
Внутри блока записываются
матем. формулы и операции для
обработки данных.
Проверка условия.
Внутри блока записываются
логические условия. Имеет два
выхода Да(+) и Нет(-).
Направление.

12. Линейный алгоритм – это алгоритм, шаги
которого выполняются последовательно
друг за другом. (Пример: алгоритм сбора
портфеля).

13. Задача
Вычислить периметр произвольного треугольника по
его трем сторонам.
Решение:
1 этап: Постановка задачи.
Исходные данные: А, B, C – стороны произвольного
треугольника
Выходные данные: P – периметр треугольника.
2 этап: Математическая модель.
P=A+B+С

14. 3 этап: Составление алгоритма
3 этап: Алгоритм.
Начало
Ввод
A, B, C
P=A+B+C
Вывод
P
Конец

15. Базовая структура линейного алгоритма:
Начало
Серия команд 1
Серия команд 2
Серия команд N
Конец

16. Задание:
Нарисовать в Приложении PAINT ракету
и описать алгоритм построения
(словесно).

17. Вспомните:
Что такое алгоритм?
Приведите примеры алгоритмов.
Что такое исполнитель?
Приведите примеры исполнителей.

18. Формы записи
алгоритмов

19. Будем рассматривать
алгоритмы, исполнителем
которых является человек.

20. Запись алгоритмов при решении
задачи
Нумерованный Блок -
Таблица
список схема

21. Блок - схема
Геометрические фигуры,
обозначающие шаги
алгоритма:

22. Овал
Обозначаемый
Изображение шаг алгоритма
Начало или
конец

23. Параллелограмм
Обозначаемый
Изображение шаг алгоритма
Ввод или
вывод

24. Ромб
Обозначаемый
Изображение шаг алгоритма
Нет Принятие
Да
решения

25. Прямоугольник
Обозначаемый
Изображение шаг алгоритма
Выполнение
действия

26. Стрелки
Связывают фигуры, задают порядок выполнения
соответствующих шагов

27. Пример алгоритма:
действия человека при переходе улицы
Начало
Подойти к
переходу
Дождаться
зеленого света
Перейти улицу
Конец

30. Правильный алгоритм:
1.Налить в чайник воду.
2. Зажечь спичку.
3. Открыть кран газовой горелки.
4. Поднести спичку к горелке.
5. Поставить чайник на плиту.
6. Ждать, пока вода закипит.
7. Выключить газ.

31. 1. Алгоритм Евклида
2. Решето Эратосфена
3. Длинные числа
4. Целочисленная оптимизация

32. Тема 1. Алгоритм Евклида

33. Вычисление НОД
НОД = наибольший общий делитель двух
натуральных чисел – это наибольшее
число, на которое оба исходных числа
делятся без остатка.
Перебор:
ИЛИ
k = a; // или k = b;
while ( a % k != 0 ||
b % k != 0 )
k --;
printf ("НОД(%d,%d)=%d", a, b, k);
много операций для больших чисел
33

34. Алгоритм Евклида
НОД(a,b)= НОД(a-b, b)
= НОД(a, b-a)
Заменяем большее из двух чисел разностью
большего и меньшего до тех пор, пока они не Евклид
станут равны. Это и есть НОД. (365-300 до. н. э.)
Пример:
НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7)
= НОД (7, 7) = 7
много шагов при большой разнице чисел:
НОД (1998, 2) = НОД (1996, 2) = … = 2
34

35. Модифицированный алгоритм Евклида
НОД(a,b)= НОД(a%b, b)
= НОД(a, b%a)
Заменяем большее из двух чисел остатком от деления
большего на меньшее до тех пор, пока меньшее не станет
равно нулю. Тогда большее — это НОД.
Пример:
НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7
Еще один вариант:
НОД(2·a,2·b)= 2·НОД(a, b)
НОД(2·a,b)= НОД(a, b) // при нечетном b
35

36. Реализация алгоритма Евклида
Рекурсивный вариант: Без рекурсии:
int NOD ( int a, int b ) int NOD ( int a, int b )
{ {
if ( a == b ) return a; while ( a != b )
if ( a < b ) if ( a > b ) a -= b;
return NOD ( a, b-a ); else b -= a;
else return NOD ( a-b, b ); return a;
} }
int NOD ( int a, int b ) int NOD ( int a, int b )
{ {
if ( a*b == 0 ) return a + b; while ( a*b != 0 )
if ( a < b ) if ( a > b ) a = a % b;
return NOD ( a, b%a ); else b = b % a;
else return NOD ( a%b, b ); return a + b;
} }
? Почему return a+b?
36

37. Тема 2. Решето Эратосфена

38. Поиск простых чисел
Простые числа – это числа, которые делятся только на себя и на 1.
Применение:
1) криптография;
2) генераторы псевдослучайных чисел.
Наибольшее известное (сентябрь 2006):
232582657 − 1 (содержит 9 808 358 цифр).
Задача. Найти все простые числа в интервале от 1 до заданного N.
Простое решение:
for ( i = 1; i <= N; i++ ) {
isPrime = 1;
? Как уменьшить число
шагов внутреннего цикла?
for ( k = 2; k*k < i i; k++ )
k <=
if ( i % k == 0 ) { k <= i k*k <= i
?
isPrime = 0;
break; Как оценить число
} операций?
if ( isPrime )
printf("%dn", i); O(N2) растет не быстрее N2
}
38

39. Решето Эратосфена
2 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Алгоритм:
1) начать с k = 2;
2) «выколоть» все числа через k, начиная с 2·k; Эратосфен Киренский
(Eratosthenes, Ερατοσθδνη)
3) перейти к следующему «невыколотому» k; (ок. 275-194 до н.э.)
4) если k·k <= N, то перейти к шагу 2;
5) напечатать все числа, оставшиеся «невыколотыми».
Новая версия – решето Аткина .
высокая скорость, количество операций
O((N·log N)·log log N )
нужно хранить в памяти все числа от 1 до N
39

40. Реализация
Массив A[N+1], где
A[i]=1, если число i не «выколото»,
A[i]=0, если число i «выколото».
// сначала все числа не выколоты
for ( i = 1; i <= N; i ++ )
A[i] = 1;
// основной цикл
for ( k = 2; k*k <= N; k ++ )
if ( A[k] != 0 )
for ( i = k+k; i <= N; i += k ) A[i] = 0;
// выводим оставшиеся числа
for ( i = 1; i <= N; i ++ )
if ( A[i] == 1 )
printf ( "%dn", i );
40

41. Тема 3. Длинные числа

42. Что такое длинные числа?
Задача. Вычислить (точно)
100! = 1·2·3·...·99·100
Проблема:
это число содержит более 100 цифр…
? Сколько нулей в конце этого числа?
? Какая последняя ненулевая цифра?
Решение:
хранить цифры в виде массива, по группам (например, 6
цифр в ячейке).
? Сколько ячеек нужно? 100! < 100100
201 цифра
201/6 ≈ 34 ячейки
42

43. Хранение длинных чисел
1234 568901 734567 =
= 1234·10000002 +
568901·10000001 +
? На что это
похоже?
734567·10000000
Хранить число по группам из 6 цифр – это значит
представить его в системе счисления с основанием
d = 1000000.
Алгоритм: {A} – длинное число,
хранящееся как массив
{A} = 1;
for ( k = 2; k <= 100; k ++ )
{ A} = {A} * k; умножение
длинного числа на
... // вывести { A} «короткое»
43

44. Умножение длинного числа на короткое
a2 a1 a0
1234 568901 734567
× 3 k
3703 706705 203701
c2 c1 c0
734567·3 = 2 203701 c0 = ( a0·k + 0) % d
r1 = ( a0·k + 0) / d
перенос, r1 c0
c1 = ( a1·k + r1) % d
568901·3 + 2 = 1 706705 r2 = ( a1·k + r1) / d
r2 c1
c2 = ( a2·k + r2) % d
1234·3 + 1 = 3703 r3 = ( a2·k + r2) / d
c2
...
44

45. Вычисление 100!
const long d = 1000000L; // основание системы
long A[40] = {1}, // A[0]=1, остальные A[i]=0
s, r; // произведение, остаток
int i, k, len = 1; // len – длина числа
пока не кончились
for ( k = 2; k <= 100; k ++ ) {
цифры числа {A} или
i = 0; есть перенос
r = 0;
while ( i < len || r > 0 ) {
s = A[i]*k + r;
A[i] = s % d; // остается в этом разряде
r = s / d; // перенос
i ++;
}
len = i; // новая длина числа
}
? Где результат?
? Можно ли брать другое d?
45

46. Как вывести длинное число?
«Первая мысль»:
for ( i = len-1; i >= 0; i -- )
printf ( "%ld", A[i] );
? Что плохо?
Проблема:
как не потерять первые нули при выводе чисел, длина
которых менее 6 знаков?
Решение:
1) составить свою процедуру;
2) использовать формат "%.6ld"!
for ( i = len-1; i >= 0; i -- )
if ( i == len-1 ) printf ( "%ld", A[i] );
else printf ( "%.6ld", A[i] );
46

47. Задания
"4": Составить программу для вычисления
99!! = 1·3·...·97·99
"5": То же самое, но написать свою процедуру для вывода
(не использовать формат "%.6ld").
“6": Написать программу для умножения двух длинных
чисел (ввод из файла).
“7": Написать программу для извлечения квадратного
корня из длинного числа (ввод из файла).
47

48. Тема 4. Целочисленная
оптимизация

49. Задачи целочисленной оптимизации
Оптимизация:
f ( x) → min при заданных ограничениях
Целочисленная оптимизация:
x – вектор (массив) целых чисел
Комбинаторная оптимизация:
x – вектор (массив) целых чисел, причем все его
элементы принадлежат заданному набору чисел
при малом количестве вариантов можно решить
простым перебором
при большом количестве вариантов на решение
перебором может потребоваться огромное время
(для ряда задач другие алгоритмы неизвестны)
49

50. Задача коммивояжера
Задача коммивояжера. Коммивояжер (бродячий торговец) должен
выйти из первого города и, посетив по разу в неизвестном порядке
города 2,3,...N, вернуться обратно в первый город. В каком
порядке надо обходить города, чтобы замкнутый путь (тур)
коммивояжера был кратчайшим?
!! Это NP-полная задача, которая строго решается
Это NP-полная задача, которая строго решается
только перебором вариантов (пока)!!
только перебором вариантов (пока)
Точные методы:
1) простой перебор; большое время счета для
2) метод ветвей и границ; больших N O(N!)
3) метод Литтла;
4) …
Приближенные методы:
1) метод случайных перестановок (Matlab); не гарантируется
2) генетические алгоритмы; оптимальное
3) метод муравьиных колоний; решение
4) … 50

51. Метод случайных перестановок
Что представляет собой решение?
комбинаторна
перестановка чисел 2,3,...N. я задача
1
1 3 5 2 4 1
1
Алгоритм:
1) записать в массив x перестановку
2 3 … N
найти длину маршрута
1 2 3 … N 1
и записать ее в Lmin;
2) выбрать случайно два элемента массива x и поменять их
местами;
3) найти длину маршрута, соответствующего x и, если она меньше
Lmin, записать ее в Lmin и запомнить перестановку;
4) если число шагов меньше заданного, перейти к шагу 2.
51