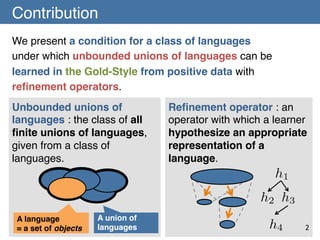
The document presents a condition under which unbounded unions of languages can be learned from positive data using refinement operators. Specifically, it introduces two theorems:
1) Theorem 1 states that a concept class (C,R,L) is learnable if it admits a refinement operator satisfying properties [A-1] to [A-3].
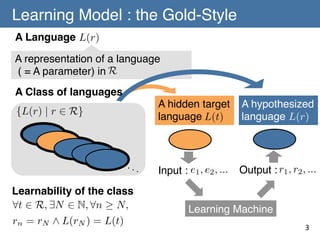
2) Theorem 2 (the contribution of the paper) states that the union concept class (C*,R*,L) is learnable if (C,R,L) admits a refinement operator satisfying [A-1] to [A-3] and additional properties [C-1] and [C-2]. This allows learning of unbounded unions of languages.


![Bounded and Unbounded Unions of
Languages
Learning bounded unions of languages!
A learner knows that data are given from finite number of
languages from the class, and also knows the upper bound
of the number of languages. (many positive results)!
eg [K. Wright 1989], [H. Arimura et al. 1995],
[T. Shinohara et al. 1995]!
!
Learning unbounded unions of languages!
A learner knows that data are given from finite number of
languages from the class. (few positive results)!
!
!
5](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-6-320.jpg)

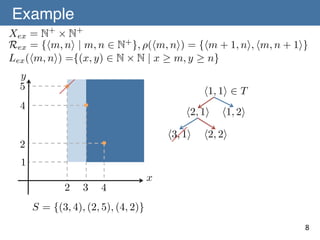
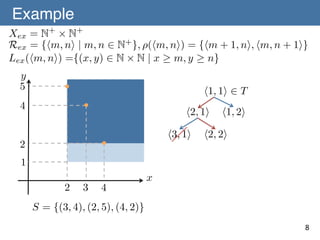
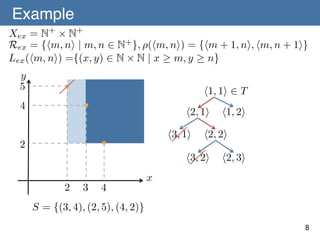
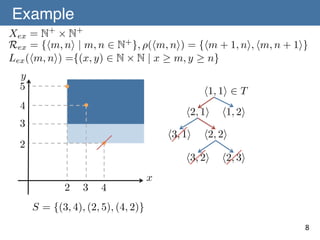
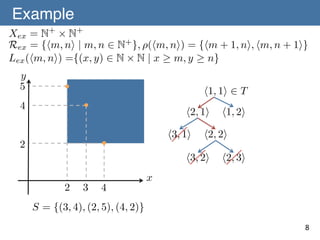
![Learnability of a Concept Space with
Refinement Operators
Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
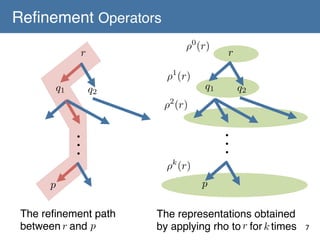
[A-1] For any p, r 2 R , if L(p) ( L(r) then there exists a
representation q 2 R such that q 2 ⇢+ (r) and L(p) = L(q)holds.!
[A-2] There is finite T ✓ R such that for any L(p) 2 C ,!
there exists t 2 T satisfying q 2 ⇢⇤ (t) and L(p) = L(q). !
[A-3] There is no infinite sequence of! L(t)
t2T
r1 , r2 , ... 2 R such that! ri+1 2 ⇢(ri )
and L(r1 ) = L(r! ) = · · ·
r
2
L(r)
for all i 2 N+.!
p
q
L(p) = L(q)
9
T : initial representation set](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-18-320.jpg)
![Learnability of a Concept Space with
Refinement Operators
Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
[A-1] For any p, r 2 R , if L(p) ( L(r) then there exists a
representation q 2 R such that q 2 ⇢+ (r) and L(p) = L(q)holds.!
[A-2] There is finite T ✓ R such that for any L(p) 2 C ,!
there exists t 2 T satisfying q 2 ⇢⇤ (t) and L(p) = L(q). !
[A-3] There is no infinite sequence of! L(t)
t2T
r1 , r2 , ... 2 R such that! ri+1 2 ⇢(ri )
and L(r1 ) = L(r! ) = · · ·
r
2
L(r)
for all i 2 N+.!
p
q
L(p) = L(q)
9
T : initial representation set](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-19-320.jpg)
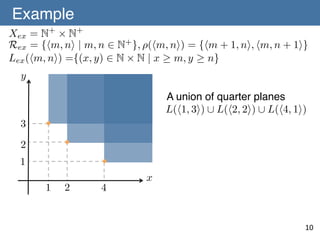

![Learnability of Unbounded Unions
Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
Theorem 2 (Our Contribution) (C ⇤ , R⇤ , L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3] and satisfies [C-1] and [C-2].!
[A-1] For any p, r 2 R , if L(p) ( L(r) then there exists a
representation q 2 R such that q 2 ⇢+ (r) and L(p) = L(q)holds.!
[A-2] There is finite T ✓ R such that for any L(p) 2 C ,!
there exists t 2 T satisfying q 2 ⇢⇤ (t) and L(p) = L(q). !
[A-3] There is no infinite sequence of L(r1 ) = L(r2 ) = · · · such
that r1 , r2 , ... 2 R and ri+1 2 ⇢(ri ) for all i 2 N+.!
12](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-22-320.jpg)
![Learnability of Unbounded Unions
Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
Theorem 2 (Our Contribution) (C ⇤ , R⇤ , L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3] and satisfies [C-1] and [C-2].!
[C-1] For any p, r 2 R , L(r) = L(p) ) r = p .!
[C-2] For any n 2 N+ , for any r0 , r1 , ..., rn 2 R ,!
L(r) ✓ L(r1 ) [ · · · [ L(rn ) , 9ri 2 {r1 , ..., rn }, L(r) ✓ L(ri )
!
L(r3 )
!
L(r3 )
L(r2 )
L(r1 )
!
L(r)
L(r)
,
!
12](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-23-320.jpg)
![Learnability of Unbounded Unions
Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
Theorem 2 (Our Contribution) (C ⇤ , R⇤ , L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3] and satisfies [C-1] and [C-2].!
˜
Lemma 4 (Our Contribution) ⇢ satisfies [A-1] to [A-3] if!
(C, R, L) admits a refinement operator ⇢ satisfying [A-1] to [A-3]
and satisfies [C-1] and [C-2].!
!
12](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-24-320.jpg)

![A Refinement Operator for Unions of
Languages
⇢(r) = {r1 , r2 , ..., rn } !
[
⇢(P ) =
˜
{P {r}} [
r2P
[
maximal r2P
Q 2 ⇢(P )
˜
(1) Q = P {r} for some r 2 P
!
!
{P [ ⇢(r) r}
!
(2) Q = P [ ⇢(r) {r} for some r 2 P !
such that L(r) 6( L(p) for any p 2 P ( r : maximal)
(2)
Lemma 3 (holds by [C-1] and [C-2] )
p1 p2 p3 p4
L(Q)
p
(
L(P )
13](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-26-320.jpg)
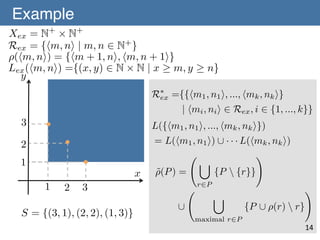
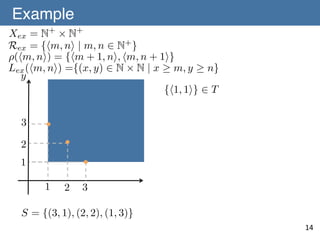
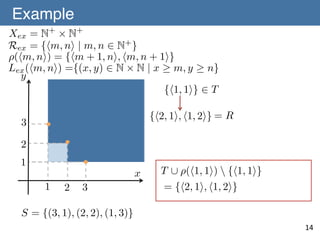
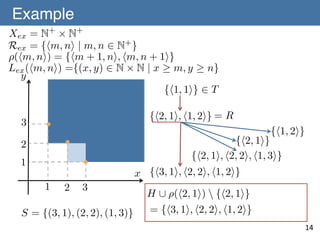
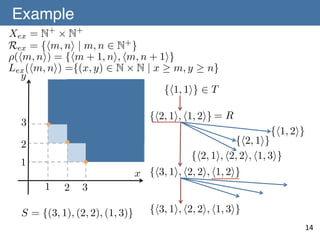
![˜
Lemma 4 (Our Contribution) ⇢ satisfies [A-1] to [A-3] if!
(C, R, L) admits a refinement operator ⇢ satisfying [A-1] to [A-3]
and satisfies [C-1] and [C-2].!
!
[A-1] For any P, Q 2 R⇤, if L(Q) ✓ L(P ) then there exists!
0
a set of hypotheses Q0 2 R⇤ such that L(Q) = L(Q ) and
Q0 2 ⇢⇤ (P ) holds.!
˜
[A-2] There is finite T ✓ R⇤such that for anyL(P ) 2 C ⇤
,!
˜
there exists S 2 T satisfying Q 2 ⇢⇤ (S) and L(P ) = L(Q).!
[A-3] There are no infinite sequence P1 , P2 , ... 2 R⇤ such that!
L(P1 ) = L(P2 ) = · · · and Pi+1 2 ⇢(Pi ) for all i 2 N+.
˜
!
15](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-32-320.jpg)
![Theorem 1 (Ouchi & Yamamoto) (C, R, L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3].!
˜
Lemma 4 (Our Contribution) ⇢ satisfies [A-1] to [A-3] if!
(C, R, L) admits a refinement operator ⇢ satisfying [A-1] to [A-3]
and satisfies [C-1] and [C-2].!
!
Theorem 2 (Our Contribution) (C ⇤ , R⇤ , L) is learnable from
positive data if (C, R, L) admits a refinement operator ⇢
satisfying [A-1] to [A-3] and satisfies [C-1] and [C-2].!
15](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-33-320.jpg)
![Concluding Remarks
Conclusion!
We have proposed a non-trivial sufficient condition ([A-1][A-3], and [C-1]-[C-2]) for learning union concept from
positive data.!
l Introducing a refinement operator for union class!
!
Future work !
There is base classes which are learnable with a refinement
operator. We check whether the union concept of this class is
also learnable from positive data using our result. !
16](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-34-320.jpg)


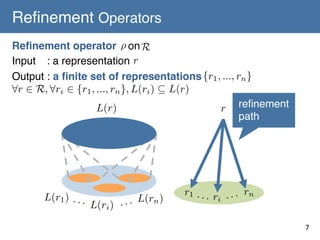
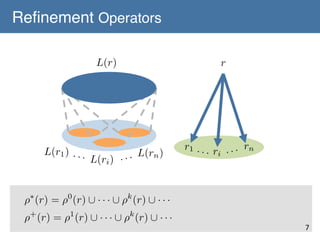
![Refinement Operators
Ouchi & Yamamoto(2010)!
Let (C, H, L) be a concept class. A mapping ρ : H → 2H is called a
refinement operator on the class if it satisfies the following three:
[R-1] For every h ∈ H, ρ(h) is recursively enumerable.
[R-2] For every h ∈ H, g ∈ ρ(h) ⇒ L(g) ⊆ L(h)
[R-3] There is no sequence h1, h2,…, hn of hypotheses such that
h1 = hn and hi+1 ∈ ρ(hi) (1 ≦ i ≦ n-1)
ρ(h)
h
g
L(g) ⊆ L(h)
No
loops](https://image.slidesharecdn.com/140106-isaim-okayama-140114193902-phpapp01/85/140106-isaim-okayama-37-320.jpg)





