This document discusses fundamentals of chemical engineering related to single-phase systems and ideal gases. It includes: 1) Descriptions of liquid and solid densities, and how they are relatively independent of temperature and pressure changes. 2) Derivation of the ideal gas equation of state from kinetic theory, and examples of using the equation to calculate properties like volume and molar flow rates. 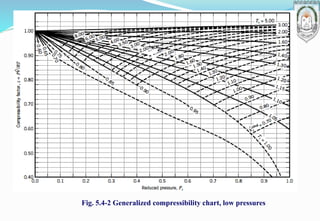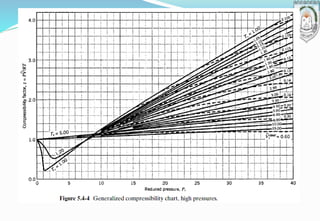3) Introduction of the compressibility factor and using generalized compressibility charts to estimate non-ideal gas behavior based on reduced temperature and pressure.

1. Fundamentals of Chemical
Engineering - II
CHPE204
PREREQUISITE: CHPE202

2. Chapter 1
Single-Phase Systems

3. LIQUID AND SOLID DENSITIES
When you heat a liquid or a solid it normally expands (i.e., its density decreases). In
most process applications, however, it can be assumed with little error that solid and
liquid densities are independent of temperature. Similarly, changes in pressure do not
cause significant changes in liquid or solid densities; these substances are therefore
termed incompressible.

4. LIQUID AND SOLID DENSITIES

5. EXAMPLE: Determination of a Solution Density

7. IDEAL GASES
The Ideal Gas Equation of State
The ideal gas equation of state can be derived from the kinetic theory of gases by
assuming that gas molecules have a negligible volume, exert no forces on one another,
and collide elastically with the walls of their container. The equation usually appears in
the form:

8. EXAMPLE: The Ideal Gas Equation of State
One hundred grams of nitrogen is stored in a container at 23.0 ºC and 3.00 psig.
1) Assuming ideal gas behavior, calculate the container volume in liters.
2) Verify that the ideal gas equation of state is a good approximation for the given conditions.
SOLUTION
The ideal gas equation of state relates absolute temperature, absolute pressure, and the quantity
of a gas in moles. We therefore first calculate:
IDEAL GASES

9. IDEAL GASES

10. Standard Temperature and Pressure
IDEAL GASES
Doing PVT calculations by substituting given values of variables into the ideal gas equation of
state is straightforward, but to use this method you must have on hand either a table of values
of R with different units or a good memory. A way to avoid these requirements is to use
conversion from standard conditions.
For an ideal gas at an arbitrary temperature and pressure ,

11. IDEAL GASES

12. EXAMPLE: Conversion from Standard Conditions
Butane (C4H10) at 360 ºC and 3.00 atm absolute flows into a reactor at a rate of 1100 kg/h.
Calculate the volumetric flow rate of this stream using conversion from standard conditions.
SOLUTION
As always, molar quantities and absolute temperature and pressure must be used.

13. EXAMPLE: Effect of T and P on Volumetric Flow Rates

14. EXAMPLE: Standard and True Volumetric Flow Rates
The flow rate of a methane stream at 285 ºF and 1.30 atm is measured with an orifice meter.
The calibration chart for the meter indicates that the flow rate is 3.95×10 SCFH (standard
cubic feet per hour [ft3 (STP)/h]). Calculate the molar flow rate and the true volumetric flow
rate of the stream.
SOLUTION

17. EXAMPLE: The Truncated Virial Equation
Two gram-moles of nitrogen is placed in a three-liter tank at –150 ºC. Estimate the tank
pressure using the ideal gas equation of state and then using the virial equation of state
truncated after the second term. Taking the second estimate to be correct, calculate the
percentage error that results from the use of the ideal gas equation at the system conditions.
SOLUTION

19. THE COMPRESSIBILITY FACTOR EQUATION OF STATE
The compressibility factor of a gaseous species is defined as the ratio

20. EXAMPLE: Tabulated Compressibility Factors
Fifty cubic meters per hour of methane flows through a pipeline at 40.0 bar absolute
and 300.0 K.
From the given reference, z = 0.934 at 40.0 bar and 300.0 K. Rearranging Equation 5.4-2c yields
SOLUTION

21. The Law of Corresponding States and Compressibility Charts
It would be convenient if the compressibility factor at a single temperature and pressure were the
same for all gases, so that a single chart or table of z( T, P) could be used for all PVT calculations.
An alternative approach is presented in this section. We will show that z can be estimated
for a species at a given temperature T and pressure P with this procedure:
1. Look up (e.g., in Table B.1) the critical temperature Tc, and critical pressure Pc, of the species.
2. Calculate the reduced temperature Tr= T/Tc, and reduced pressure Pr= P/Pc .
3. Look up the value of z on a generalized compressibility chart which plots z versus Pr for
specified values of Tr.

22. The basis for estimating in this manner is the empirical law of corresponding states, which
holds that the values of certain physical properties of a as—such as the compressibility factor
depend to great extent on the proximity of the as to its critical state. The reduced temperature
and pressure provide a measure of this proximity; the closer Tr and Pr are to 1, the closer the
gas is to its critical state. This observation suggests that a plot of z versus Tr and Pr should be
approximately the same for all substances.
The below Figure shows a generalized compressibility chart for those fluids having a critical
compressibility factor of 0.27

23. A generalized compressibility chart for those fluids

24. The procedure for using the generalized compressibility chart for PVT calculations is
as follows:

25. Fig. 5.4-2 Generalized compressibility chart, low pressures

28. EXAMPLE: The Generalized Compressibility Chart
One hundred gram-moles of nitrogen is contained in a 5-liter vessel at 20 6 C.
Estimate the pressure in the cylinder..
SOLUTION
From Table B.1, the critical temperature and pressure of nitrogen are

30. Nonideal Gas Mixtures
Whether an analytical or graphical correlation is used to describe nonideal gas behavior,
difficulties arise when the gas contains more than one species. Consider, for example, the SRK
equation of state (Equation 5.3-7)
We will illustrate PVT calculations for mixtures with a simple rule developed by Kay that utilizes
the generalized compressibility charts.

31. EXAMPLE: Kay’s Rule
A mixture of 75% H2 and 25% N2 (molar basis) is contained in a tank at 800 atm and – 70 C.
Estimate the specific volume of the mixture in L/mol using Kay’s rule.
SOLUTION