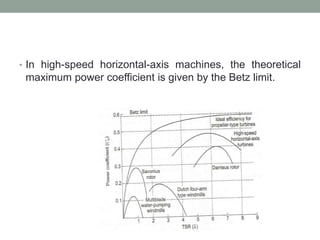
This document discusses key terms related to wind turbines such as solidity, tip speed ratio, and power coefficient. It also provides the solution to a sample problem calculating the thrust and power developed by a 3-blade wind turbine given its specifications like diameter, rotational speed, chord length, pitch angle, and wind speed. The total power produced is calculated to be 10 kW and the total thrust on the tower is calculated to be 1893.4 N. Key parameters like lift and drag coefficients are obtained from aerfoil characteristic curves and blade element theory is used to divide the blades into segments and calculate thrust and power contributions from each segment.

1. IMPORTANT TERMS
Dr. Ashwini Kumar Nayak
Asst. Professor,
School of Electrical Sciences
NIST, Berhampur

2. Solidity
• The solidity of a wind rotor is the ratio of the projected
blade area to the area of the wind intercepted.
• The projected blade area does not mean the actual blade
area.
• It is the blade area met by the wind or projected in the
direction of the wind.

3. • For Savonius rotor is naturally unity, as the wind sees no
free passage through it.
• For multiblade water-pumping windmill is around 0.7.
• For high-speed horizontal-axis machines, it lies between
0.01 and 0.1; it is same for Darrieus rotor.

4. • Solidity has a direct relationship with torque and speed.
• High-solidity rotors have high torque and low speed, and
are suitable for pumping water.
• Low-solidity rotors have high speed and low torque, and
are typically suited for electrical power generation.

5. Tip Speed Ratio
• The tip speed ratio (TSR) of a wind turbine is
where λ is the TSR (Non-dimensional), R is the radius of
the swept area (in meters), N is the rotational speed in
revolutions per second, and V∞ is the wind speed without
rotor interruption (in meters per second).
2 RN
V





6. • For the Savonius rotor and the multiblade water-pumping
windmills are generally low.
• In high-speed horizontal-axis rotors and Darrieus rotors,
the outer tip actually turns much faster than the wind
speed owing to the aerodynamic shape. Thus, the TSR
can be as high as 9.
• High-solidity rotors have low TSRs and vice versa.

7. Power Coefficient
• The power coefficient of a wind energy converter is
• Power coefficient differs from the efficiency of a wind
machine.
• Efficiency includes the losses in mechanical transmission,
electrical generation, etc.
• Power coefficient is the efficiency of conversion of wind
energy into mechanical energy to the shaft.
P
power output fromthe wind machine
C
power contained in wind


8. • In high-speed horizontal-axis machines, the theoretical
maximum power coefficient is given by the Betz limit.

9. Wind Turbine Ratings and Specifications
• Some manufacturers specify the power rating along with
the wind speed at which the power rating is obtained.
• There is no specific rule to define the rating.
• Specific rated capacity (SRC) is
• It varies between 0.2 for small rotors to 0.6 for large ones.
power rating of the genrator
SRC
rotor swept area


10. Problem
Calculate the total thrust and aerodynamic power
developed in a three-blade wind turbine at a wind velocity
(V∞) of 9 m/s. The machine specifications are as follows
Diameter=9 m, rotational speed=100 rpm, blade length= 4
m, TSR=5.23, Chord length= 0.45 m, uniform throughout
the blade, pitch angle α= 5o , no twist, distance from axis to
inner edge of blade= 0.5 m, aerofoil section= NACA 23018.

11. Solution: To apply blade theory, the length of the blade is
divided into small segments (four) of length 1m each. The
value related to the middle of each section are denoted by
the corresponding subscript.
Area of each section is 0.45×1.0=0.45m2
From Betz theory, maximum efficiency is obtained when
v=2V∞/3. Considering v=6 m/s. The rotational speed is
100/60= 1.66 rps.

12. As tan I=v/u, the values of I at each section are
1
1
1
2
1
3
1
4
6
tan 29.81
2 1.0 1.66
6
tan 15.98
2 2.0 1.66
6
tan 10.81
2 3.0 1.66
6
tan 8.15
2 4.0 1.66
o
o
o
o
I
I
I
I








 
  
 
  
 
  
 
  

13. As i=I-α, i1= 24.81o, i2= 10.98o, i3= 5.81o, and i4= 3.15o.
From the characteristic curves of the NACA 23018 aerofoil,
CL1=0.95, CD1=0.0105
CL2=1.20, CD2=0.0143
CL3=0.75, CD3=0.0092
CL4=0.46, CD4=0.0078

14. Similarly, dP2=886.14 W, dP3=1190.52 W, and
dP4=1213.38 W. So the total power=
3×(198.72+886.14+1190.52+1213.38)= 10,466 W=10 kW
The thrusts are calculated as
DFT1= 0.5×1.25×0.45 ×62 ×(1+cot2I) ×(0.95 cos I +0.0105
sin I)=33.98 N
3 2
1 0.5 1.25 0.45 6 cot 29.81(1 cot 29.81)
(0.95sin 29.81 0.0105cos29.81) 198.72
dP
W
     
  

15. • Similarly, dFT2=154.24 N, dFT3=212.94 N, and
dFT4=229.96 N. Therefore, the total thrust that tower has
to withstand at rated wind speed is 3 ×
(33.98+154.24+212.94+229.96)=1893.4 N