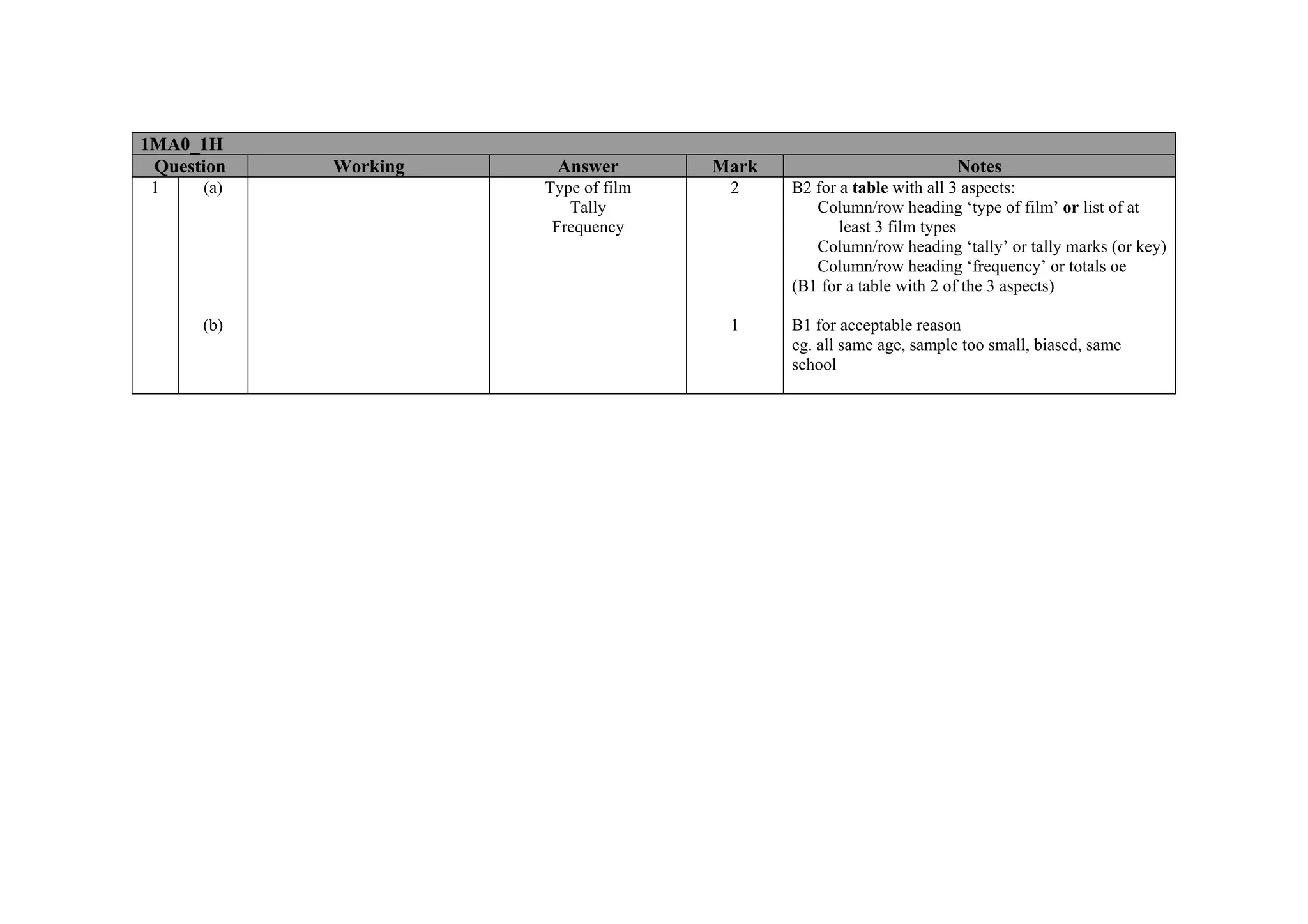
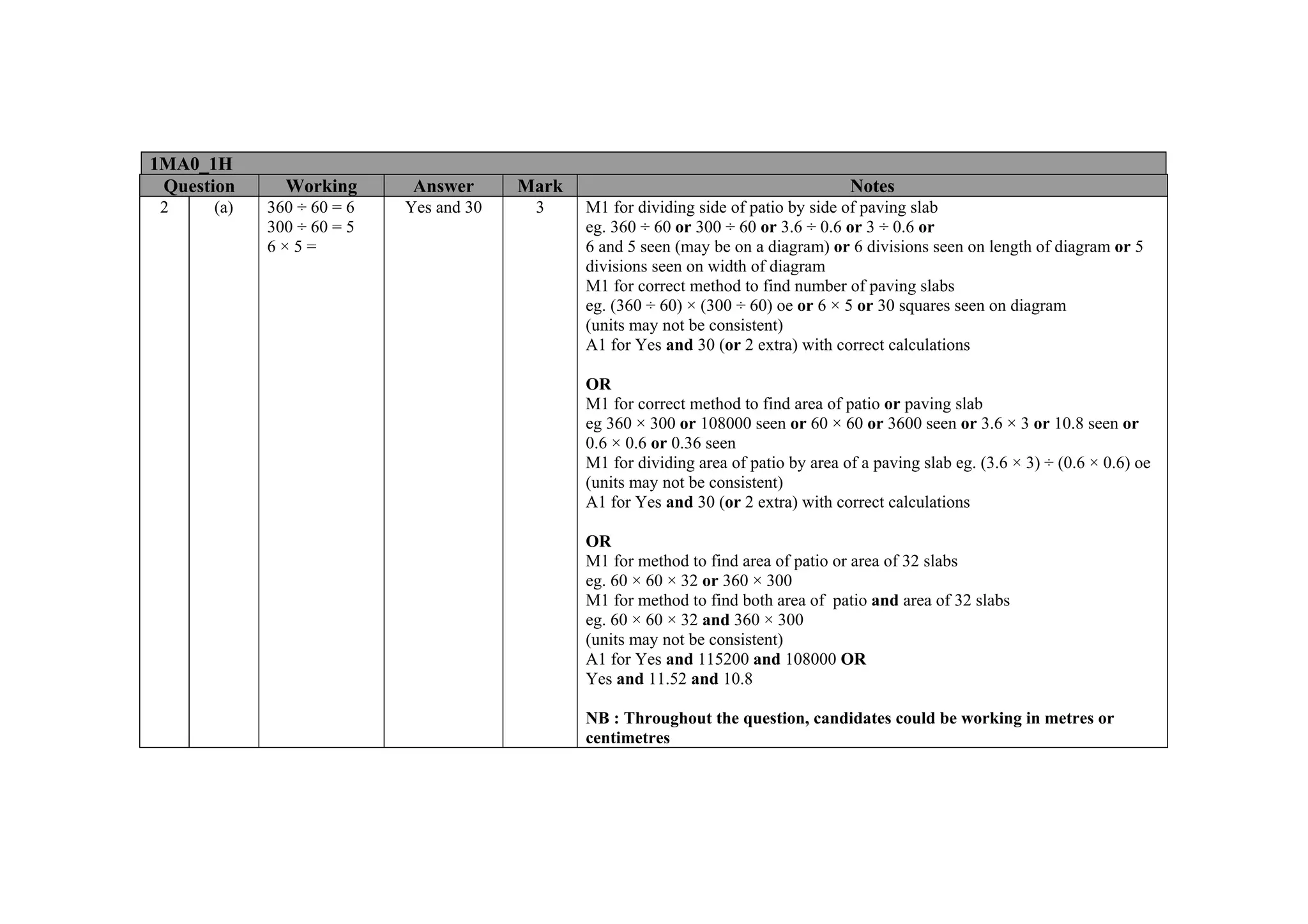
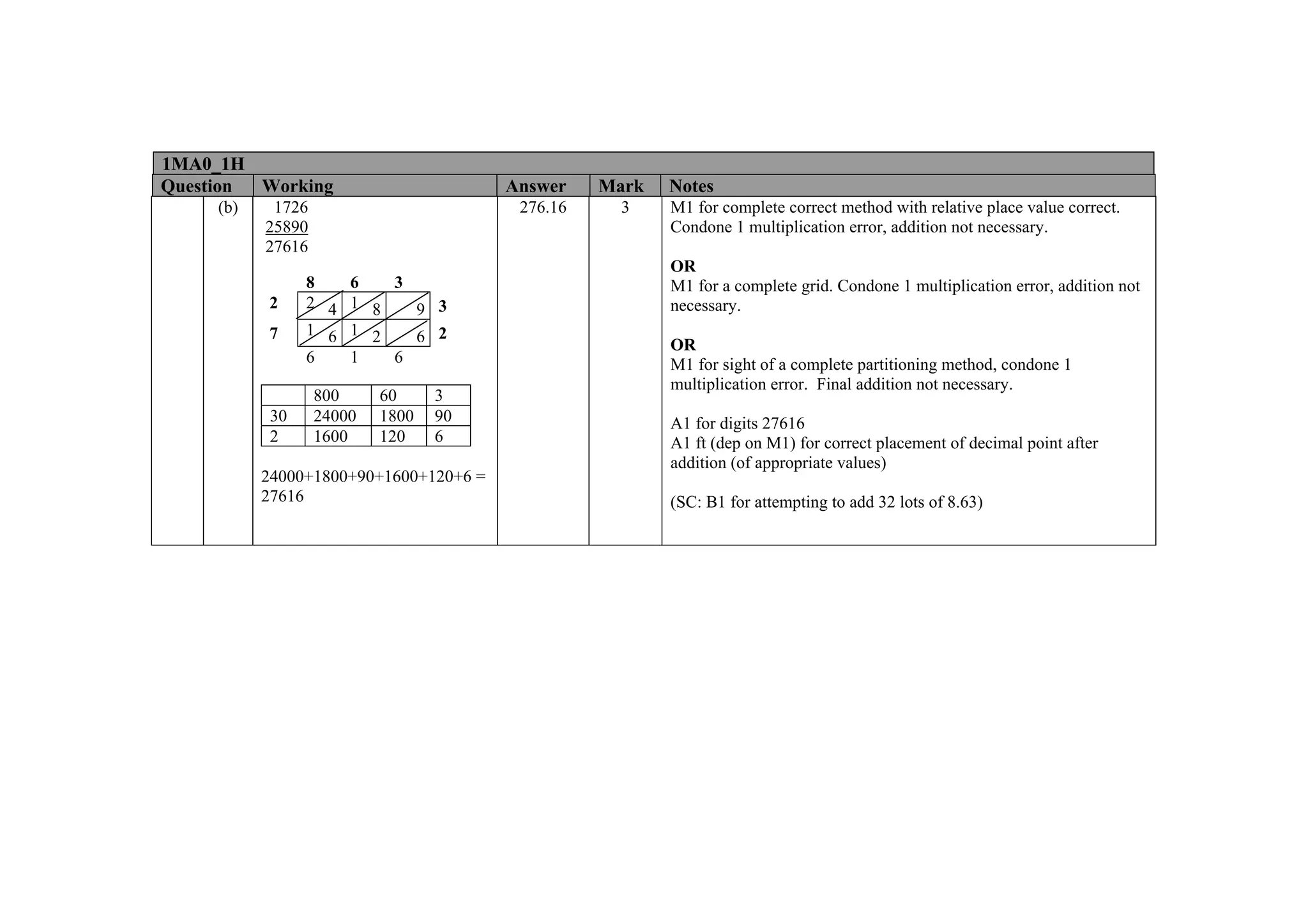
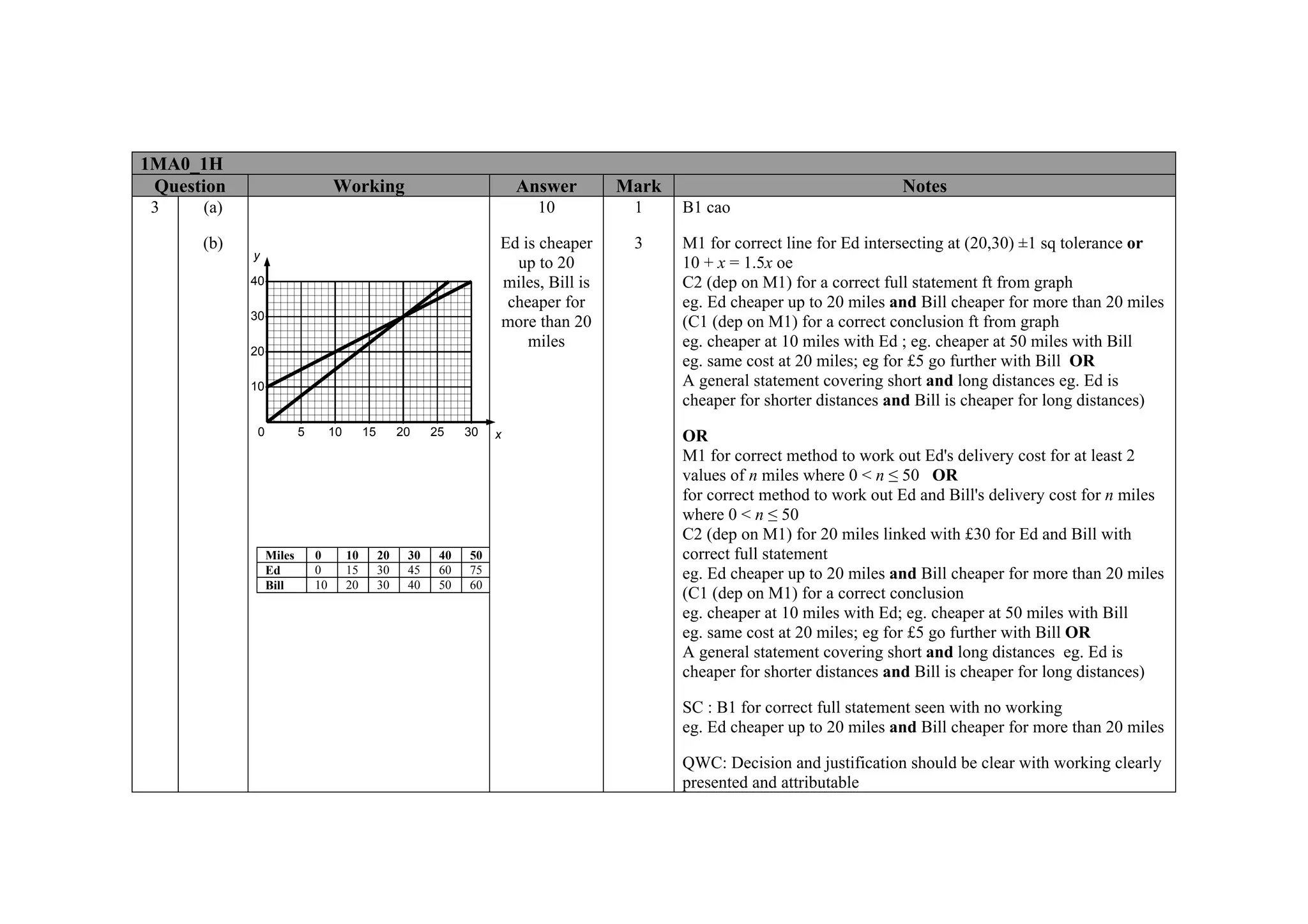
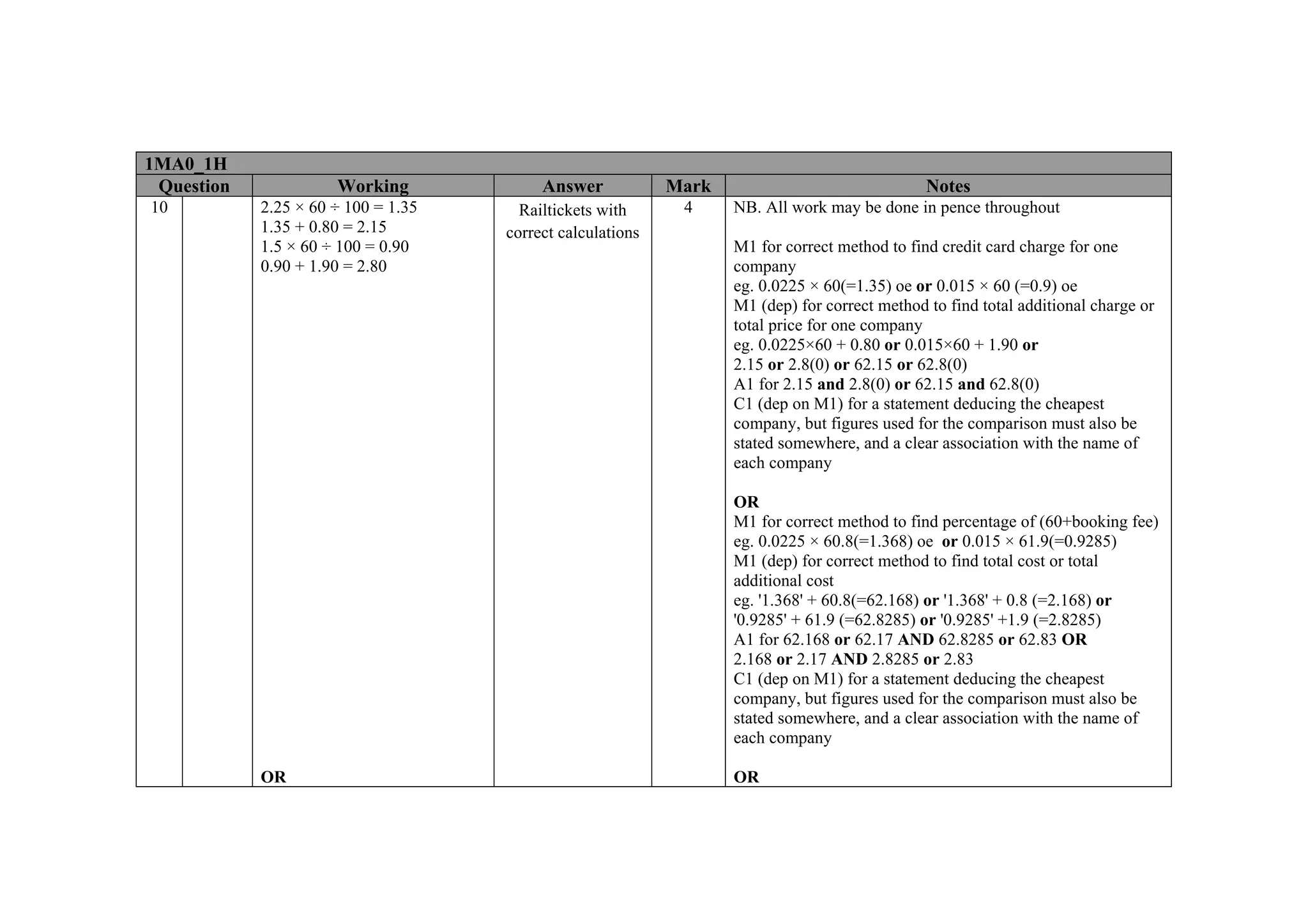
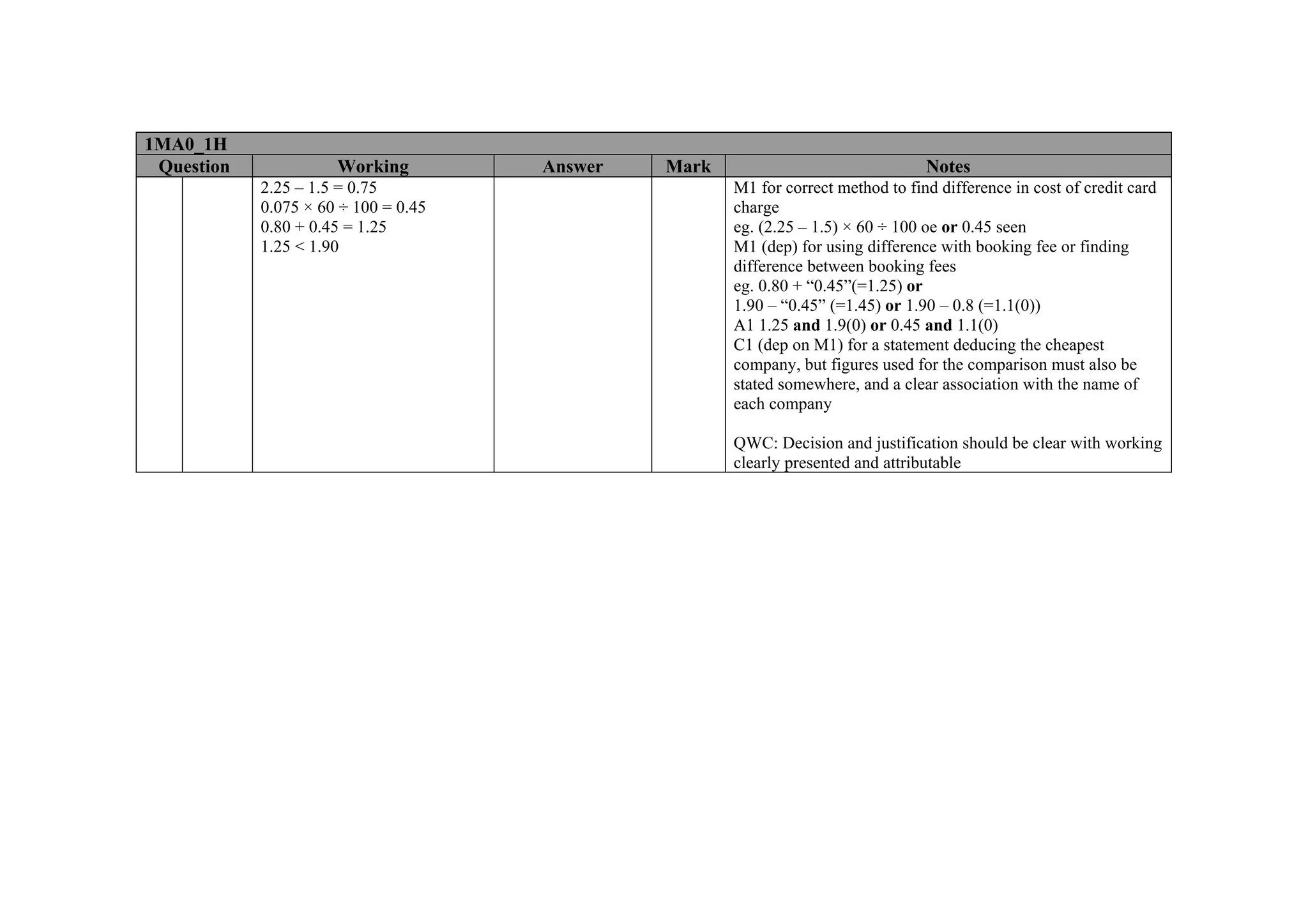
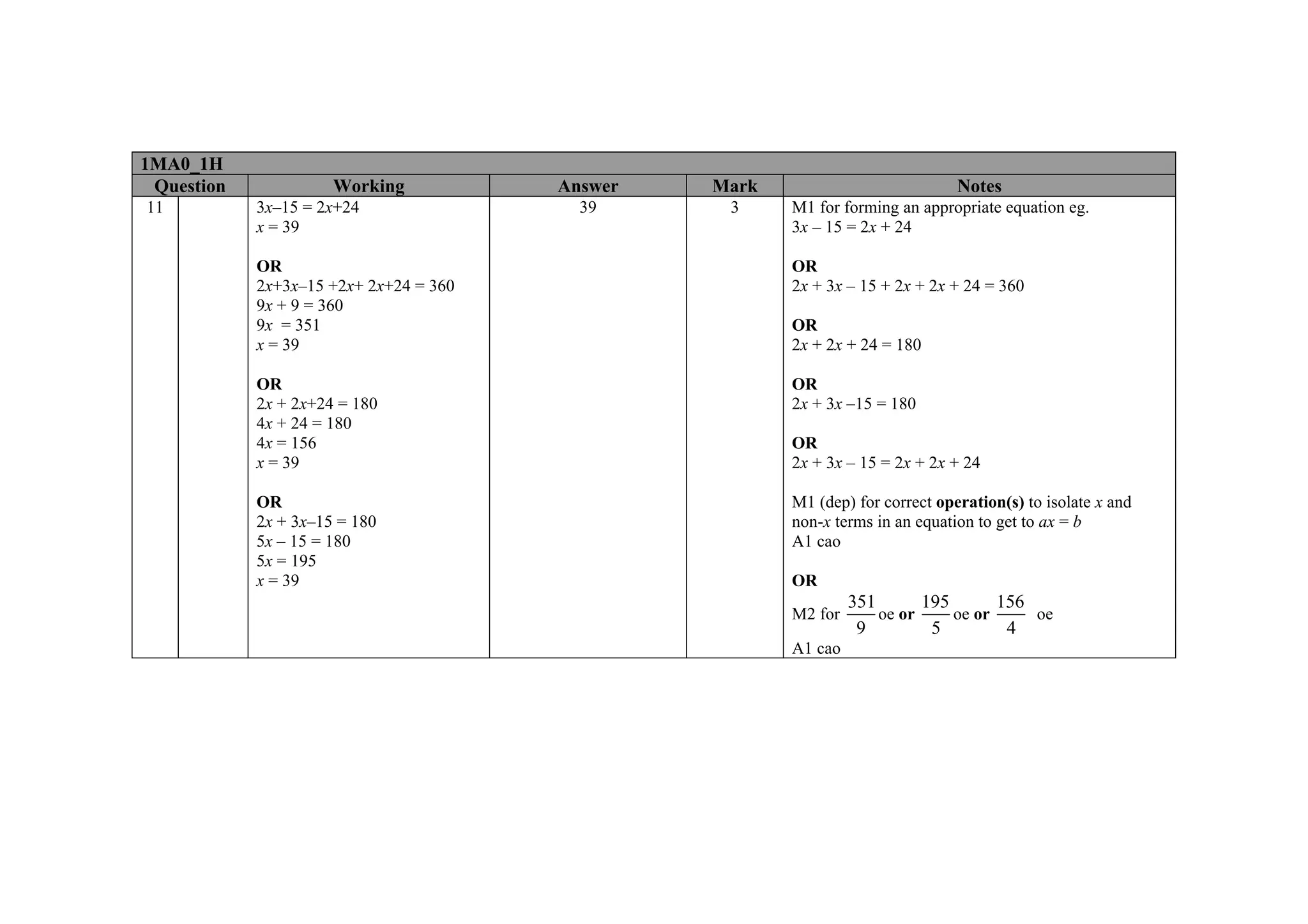
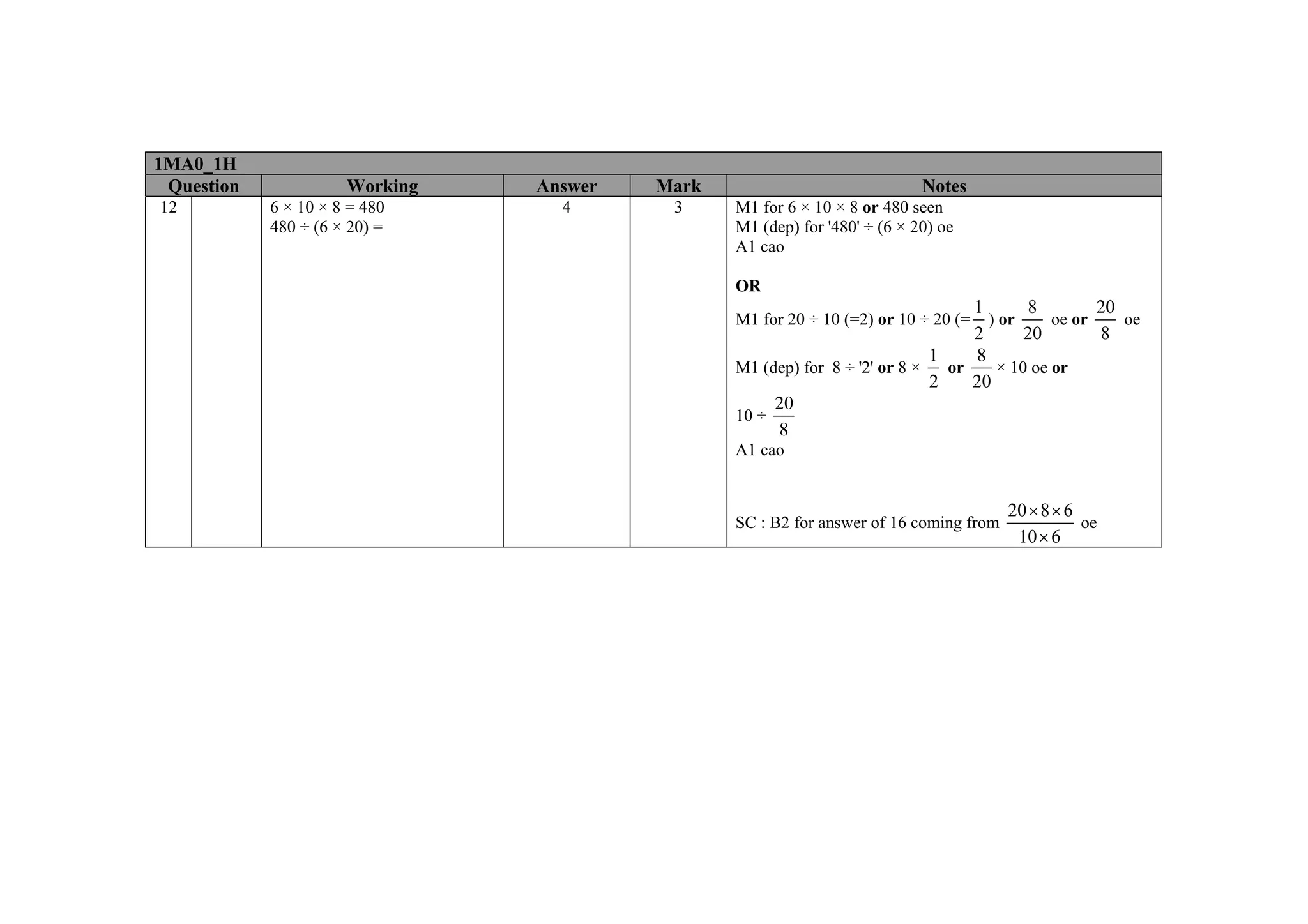
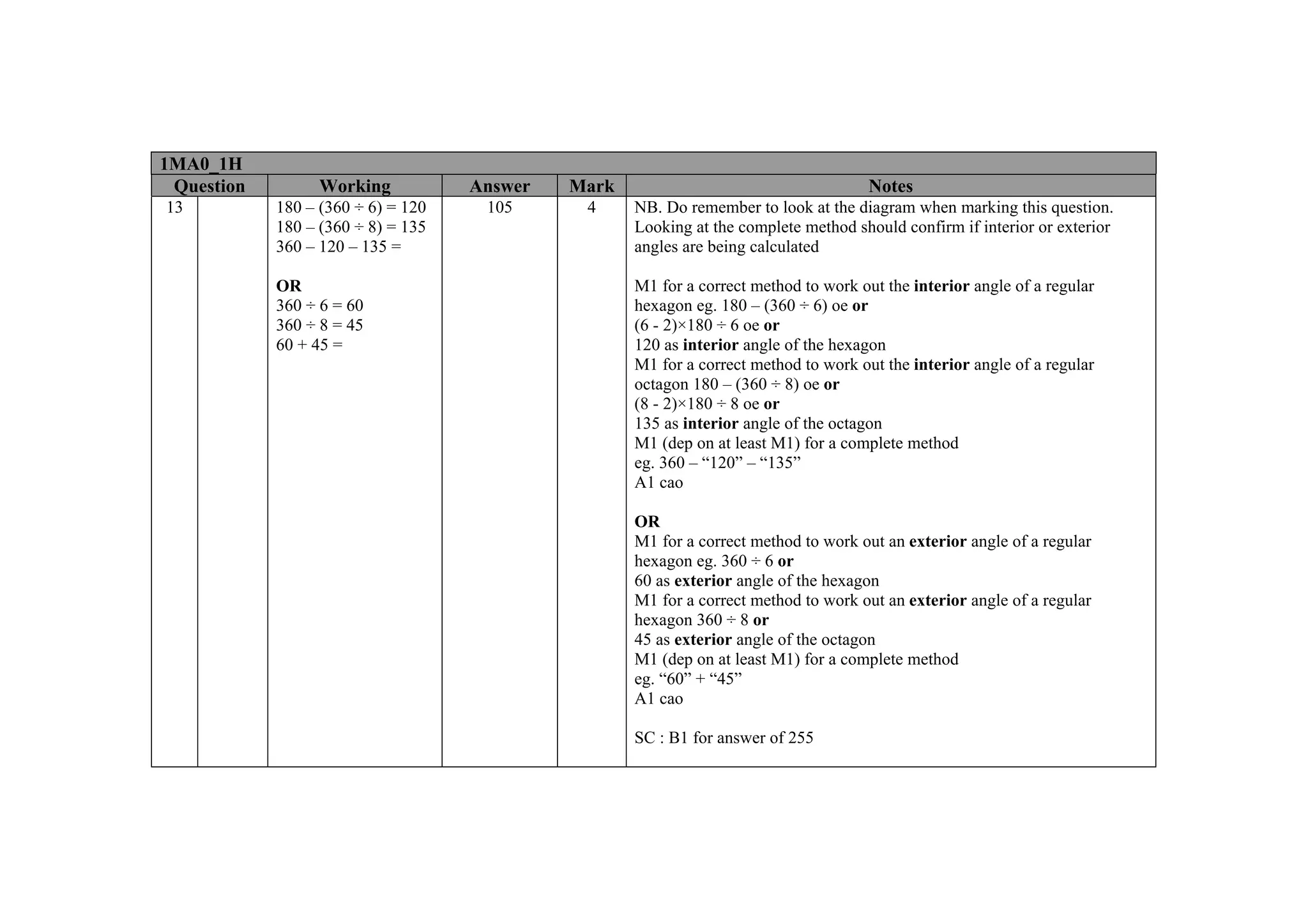
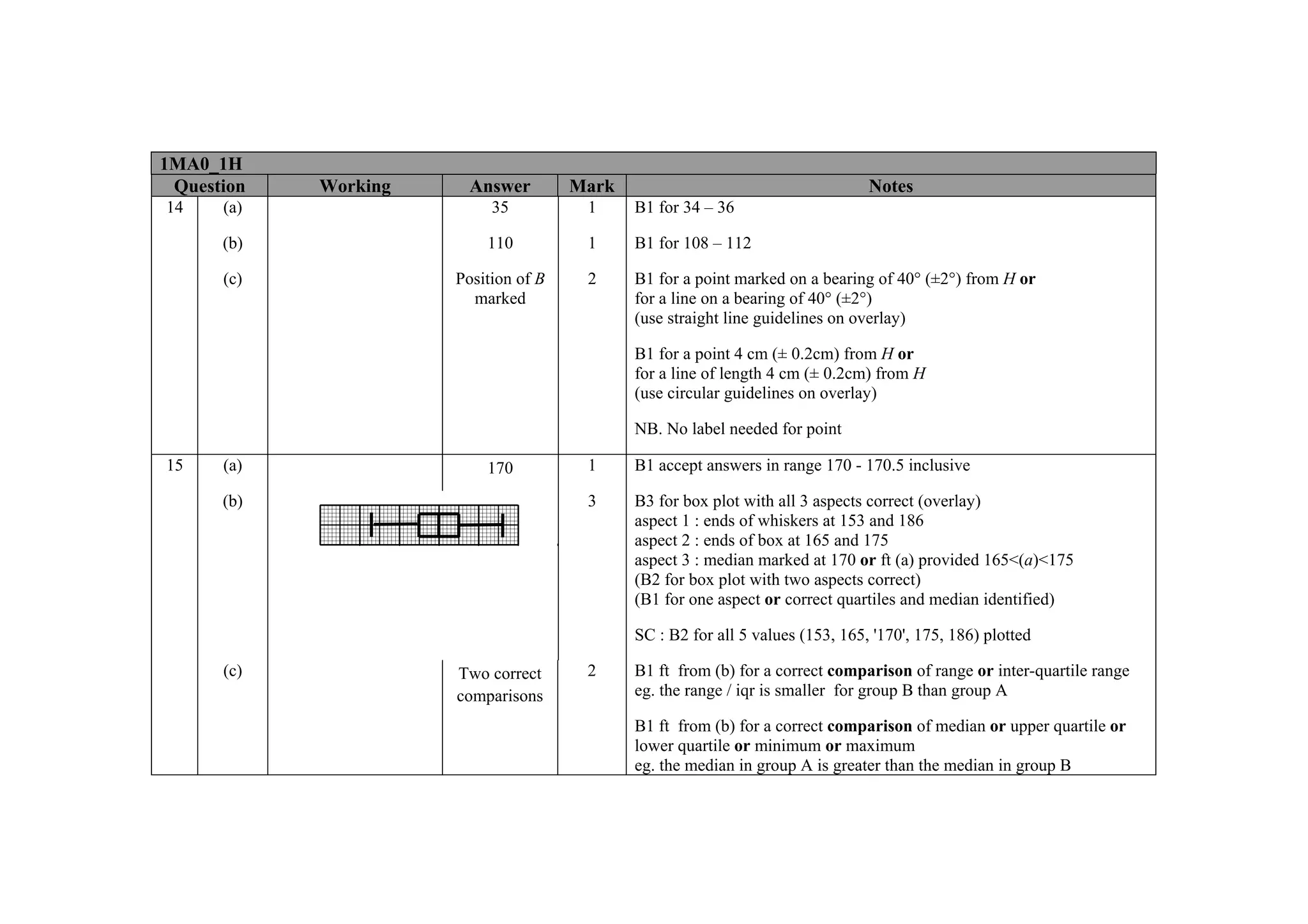
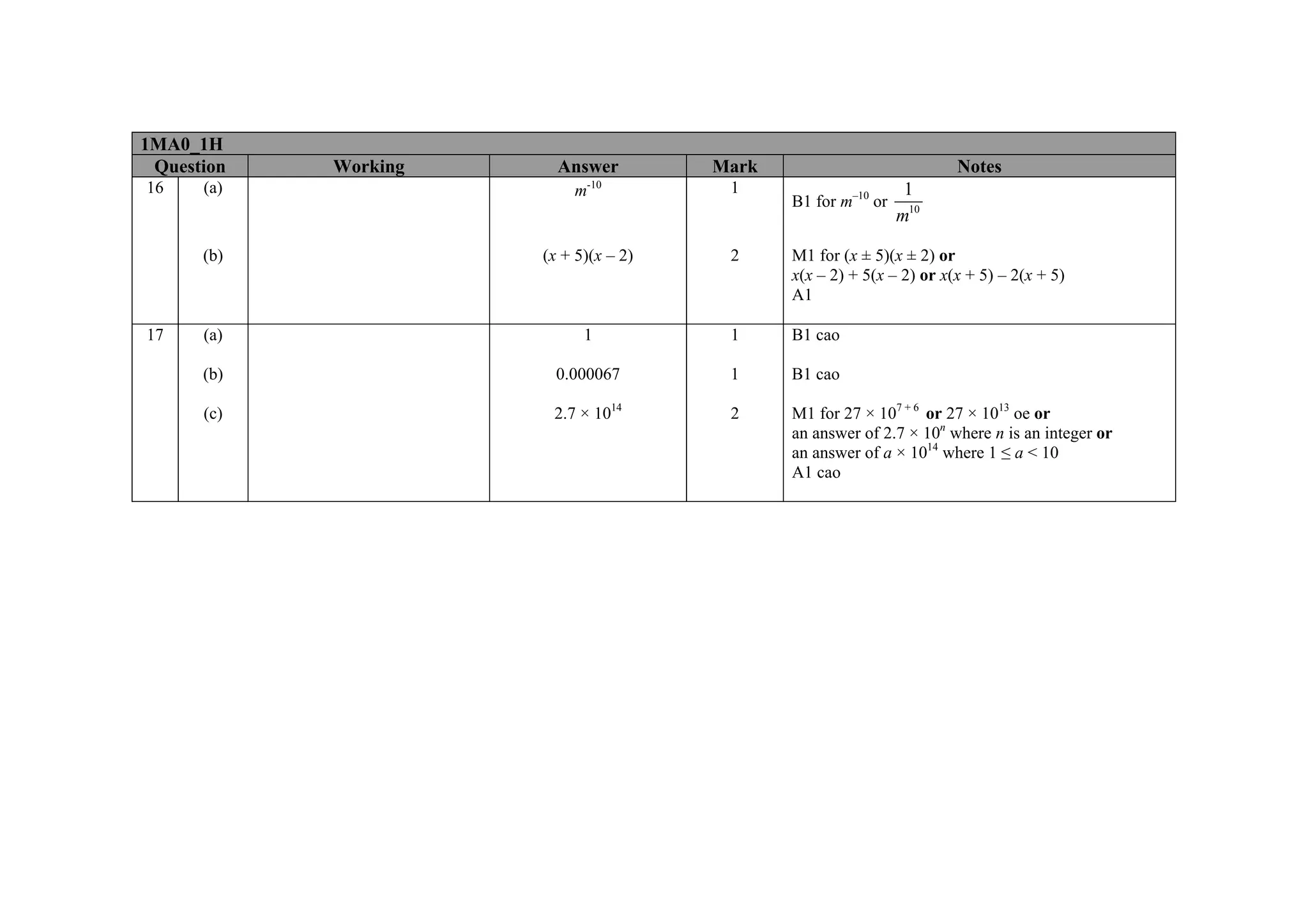
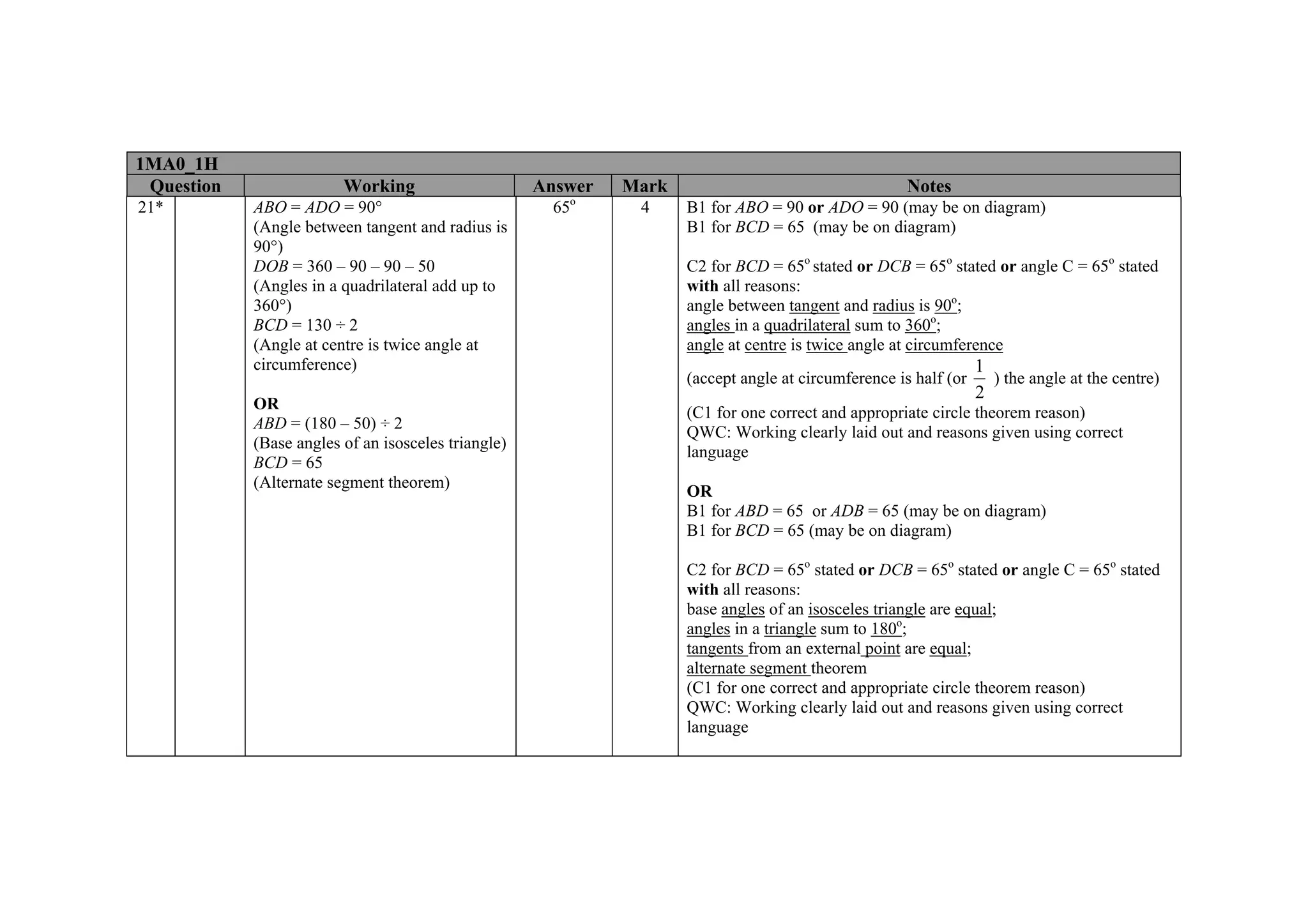
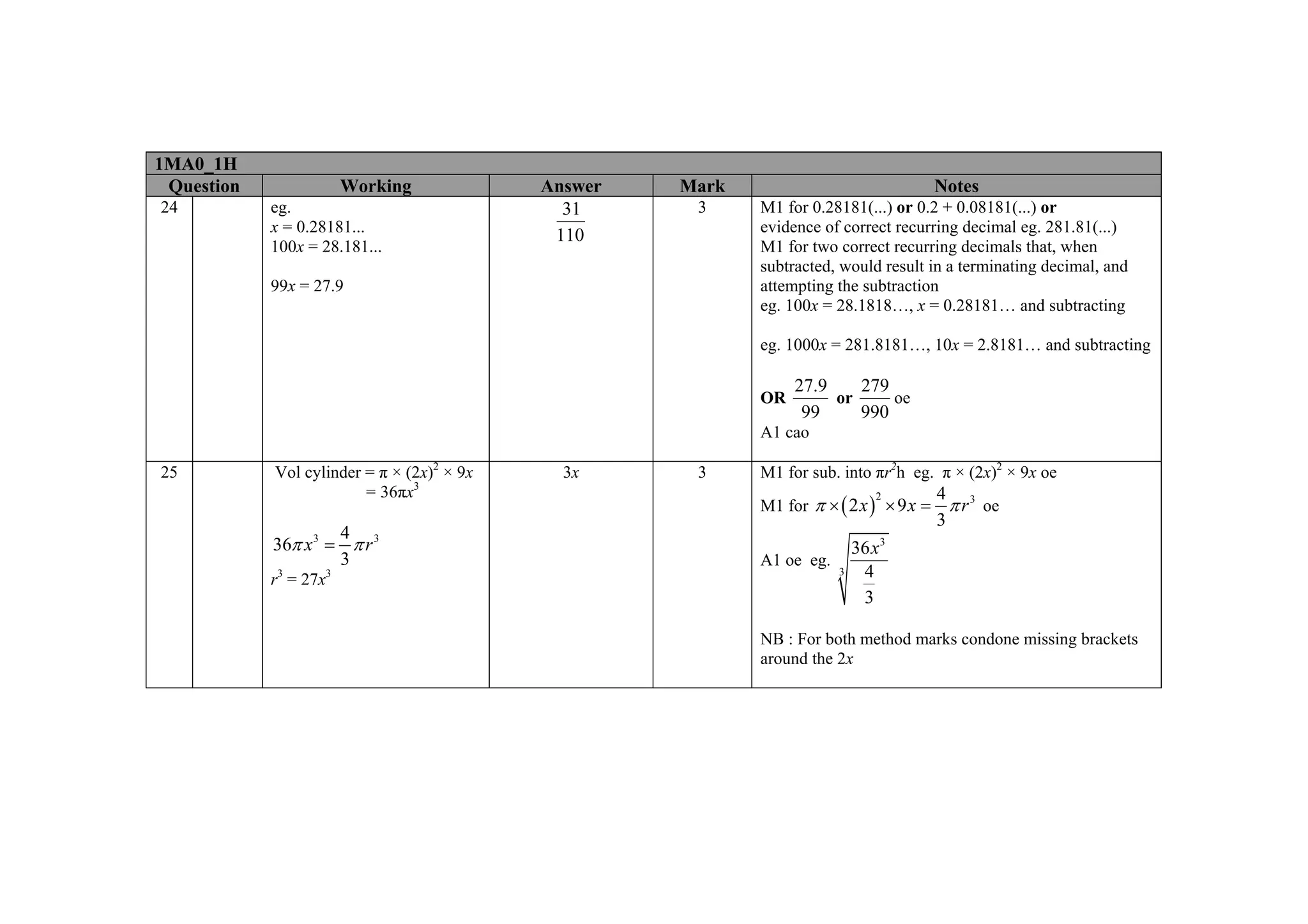
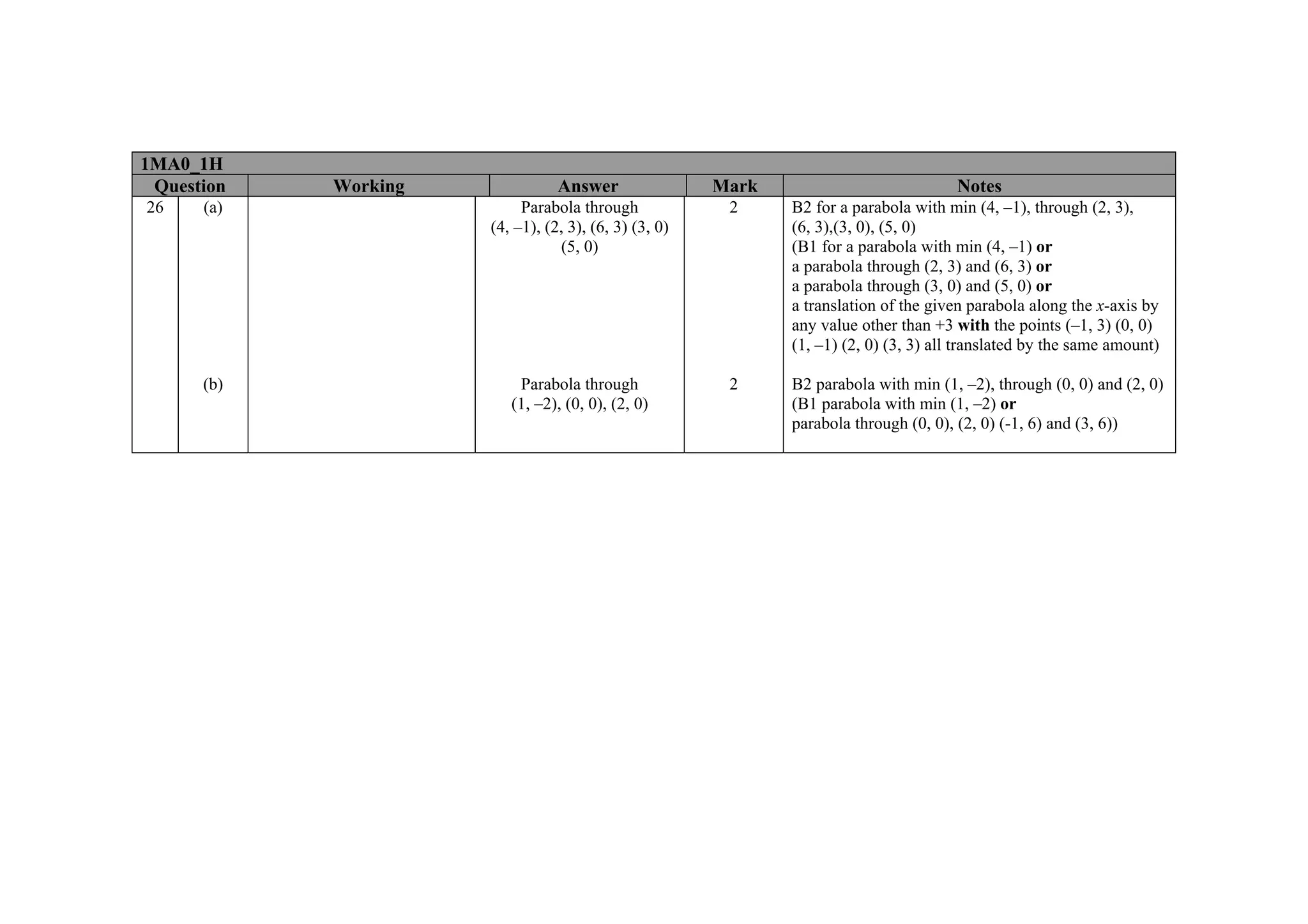
This document contains a mark scheme for a GCSE mathematics exam. It provides guidance for examiners on how to apply marks for different parts of student responses. Some key points include:
1) Examiners must mark all students equally and reward students for what they show they can do rather than penalize for omissions.
2) Full marks should be awarded if the answer matches the mark scheme.
3) Working should be considered, even if the final answer is incorrect, to award method marks where appropriate.
4) Follow through marks can be awarded if subsequent working is based on a previous correct response.
5) Marks cannot be awarded for one part of a question in another part