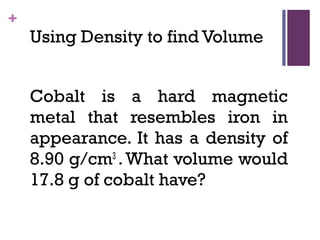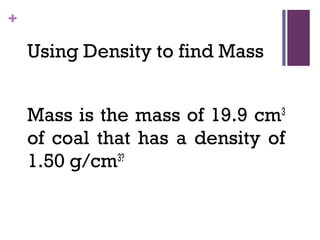This document provides an introduction to physical science. It begins by defining science and listing the main branches - biological science, physical science, and social science. Biological science deals with living things, social science deals with human behavior and societies. Physical science deals with non-living things, their composition, nature, characteristics, and changes. The main branches of physical science are then defined: chemistry studies matter and its properties/structure/changes, physics studies matter and energy/their interactions, astronomy studies the universe/heavenly bodies, geology studies Earth materials/structures/processes, and meteorology studies the atmosphere/weather/climate. 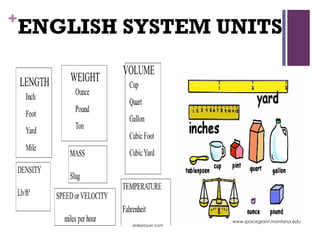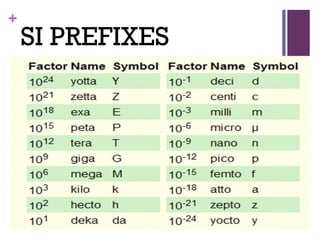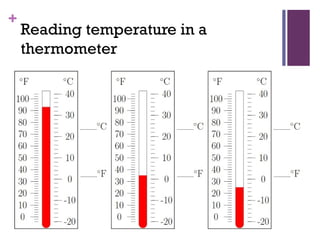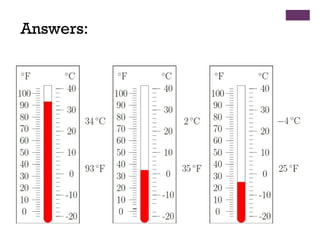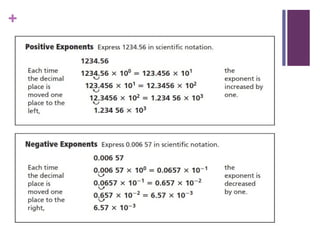The document then moves to a chapter about measurement, defining it as collecting quantitative data by

1. +
CHAPTER 1
INTRODUCTION
TO
PHYSICAL SCIENCE

2. +
SCIENCE
systematized or organized body of
knowledge based on observation,
experimentation and study.
comes from the Latin word Scientia
- knowledge or knowing

3. +
BRANCHES OF
SCIENCE
Biological Science
Physical Science
Social Science

4. +
BIOLOGICAL
SCIENCE
deals with the study
of living things
ex. Biology, Botany,
Zoology,
Ornithology

5. +
SOCIAL
SCIENCE
Study of human
behaviour and
societies
Ex. History, Economics,
Political Science

6. +
PHYSICAL
SCIENCE
deals with the study of
non-living things, their
composition, nature,
characteristics, the
changes they have
undergone and the
factors affecting these
changes

7. +
BRANCHES OF
PHYSICAL SCIENCE
 Chemistry- the
study of “matter”-
its composition,
properties,
structure and the
changes it
undergoes.

8. +
BRANCHES OF
PHYSICAL SCIENCE
 Physics- the science of matter and
energy and their interaction with each
other.

9. +
BRANCHES OF
PHYSICAL SCIENCE
 Astronomy-
study of the
universe and the
heavenly bodies.

10. +
BRANCHES OF
PHYSICAL SCIENCE
Geology- deals with
the composition of
Earth materials, Earth
structures, and Earth
processes

11. +
BRANCHES OF
PHYSICAL SCIENCE
Meteorology- study
of the atmosphere
and how processes in
the atmosphere
determines Earth’s
weather and climate

12. +
CHAPTER 2
MEASUREMENT

13. +
MEASUREMENT
Collection of quantitative
data
Made by comparing an
unknown quantity with a
standard unit
Example:The length of a
piece of string can be
measured by comparing the
string against a meter stick.
www.endlesslift.com

14. +
Every measurement is
composed of a number and
a unit.
sakai.ithaca.edu

15. + SYSTEMS OF
MEASUREMENT
ENGLISH SYSTEM- most commonly used
in the US.
Disadvantage: units are not systematically
related to each other and require
memorization.
METRIC (SI)- used by the scientist around
the world. Adopted from the French name
Le Systeme Internationale d’ Unites

16. +
ENGLISH SYSTEM UNITS
www.spacegrant.montana.edu
slideplayer.com

17. +
SI PREFIXES

18. +
www.boundless.com

19. + LENGTH
 Measurement of anything from end to end
 How long an objects is
 The basis of length units for the metric system is
the meter.
1 inch = 2.54 centimeters = 25.4 millimeters
1 foot = 30.48 centimeters
1 yard = 0.91 meters
1 mile = 1.6 kilometers
1 millimeter = 0.04 inches
1 centimeter = .39 inches = 0.0325 feet
1 meter = 3.28 feet
1 kilometer = 0.62 miles

20. + MASS ANDWEIGHT
 Mass and weight are not the same thing. Although we often
use the interchangeably, each one has a specific definition
and usage.
 Mass- measure of the amount of matter in an object.The
mass of an object is independent of its location.The basic
unit form mass is kilogram (kg) .
 Weight- force of attraction between the object and the
earth’s gravity.The weight of an object can vary from place
to place and changes with its location on the Earth.

21. +
DEVICES USED IN
MEASURING
UNITS CONVERSION

22. +
TIME
Interval between two occurrences.The
basic unit for time is second.
• 1 minute (60 seconds)
• 1 hour (60 minutes, or 3,600 seconds)
• 1 day (24 hours, or 86,400 seconds)
• 1 week (7 days, or 604,800 seconds)
• 1 month (28-31 days, or 2,419,200-
2,678.400 seconds)
• 1 year (about 365.25 days, or about
31,557,600 seconds)

23. + TEMPERATURE
 Measure of how hot or cold an object is.The basic unit for
temperature is Kelvin.

24. +
 To convert from Celsius to Fahrenheit
 To convert from Fahrenheit to Celsius
o
C= o
F – 32/ 1.8
 To convert from Celsius to Kelvin
K= o
C + 273
 To convert from Kelvin to Celsius
o
C= K - 273
o
F= 1.8 (o
C) + 32

25. +
Reading temperature in a
thermometer

26. Answers:

27. +
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
An easy way to move within the metric system is
by moving the decimal point one place for each
“step” desired
Example: change meters to centimeters
1 meter = 10 decimeters = 100 centimeters
or
1.00 meter = 10.0 decimeters = 100. centimeters
CONVERTING UNITS: METRIC TO
METRIC

28. +
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
Now let’s try this example from meters to
kilometers:
16093 meters = 1609.3 decameters = 160.93 hectometers = 16.093
kilometers
So for every “step” from the base unit to
kilo, we moved the decimal 1 place to the
left
(the same direction as in the diagram
below)

29. +
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
If you move to the left in the diagram,
move the decimal to the left
If you move to the right in the
diagram, move the decimal to the
right

30. +
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
Now let’s start from centimeters
and convert to kilometers
400000 centimeters = ______kilometers

31. +
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
Kilo
(1000)
Hecto
(100)
Deca
(10)
Base Units
meter
gram
liter
deci
(1/10)
centi
(1/100)
milli
(1/1000)
 Now let’s start from meters and convert to centimeters
5 meters = _____ centimeters
• Now let’s start from kilometers and convert to meters
.3 kilometers = ______ meters

32. +
 A conversion factor is a term that
converts a quantity in one unit to a
quantity in another unit.
 Factor-label method is the
process of using conversion factors
to convert a quantity in one unit to
a quantity in another unit.
CONVERTING UNITS: USING
THE FACTOR-LABEL METHOD

33. +
 The conversion factor
must relate the two
quantities in questions.
The conversion factor
must cancel out the
unwanted unit.

34. +
Let’s say we want to convert 130 lb to
kilograms.
130 lb X conversion factor= ____ kg
Two possible conversion factors:
2.21 lb or 1 kg__
1 kg 2.21 lb

35. +
130 lb x 1 kg__ = 59 kg
2.21 lb
Pound (lb) must be the denominator
to cancel the unwanted unit (lb) in the
original quantity.

36. +
TRY…
a. 32 inches to centimeter
b. 6250 ft to km
c. 25 L to dL

37. +
DERIVED UNITS

38. +
AREA
amount of two-dimensional space taken up
by an object
the size of a surface
Area of rectangle(A) = length(l) x width(w)
Area of circle (A)= π × r2

39. + This table lists different area units, and
values that will help you change units of
area measurements:

40. + VOLUME
1 L = 10 dL
1 L = 1000 mL
1 000 L = 1 m3
1 dL = 100 mL
1 mL = 1 cm3
= 1 cc
1 cc = .001 L
1 L= 1 000 cc

41. + DENSITY
 Mass per unit volume
 Units: g/cc , g/cm3
, g/mL
 Formula:

42. +
Sample Problem: Calculating
Density
A piece of beeswax with a
volume of 8.50 cm3
is found to
have a mass of 8.06 g. What is the
density of the beeswax?

43. +
Using Density to find Volume
Cobalt is a hard magnetic
metal that resembles iron in
appearance. It has a density of
8.90 g/cm3
.What volume would
17.8 g of cobalt have?

44. +
Using Density to find Mass
Mass is the mass of 19.9 cm3
of coal that has a density of
1.50 g/cm3?

45. + SCIENTIFIC NOTATION
 Scientific notation is a way of expressingScientific notation is a way of expressing
really big numbers or really smallreally big numbers or really small
numbers.numbers.
Scientific Notation always has two parts:
 N is the coefficient ( A number between 1 andN is the coefficient ( A number between 1 and
9.9999…)9.9999…)
 X is an exponent, which can be any positive orX is an exponent, which can be any positive or
negative whole number.negative whole number.
N x 10N x 10xx

46. +
Writing Scientific Notation
 Place the decimal point so that there isPlace the decimal point so that there is oneone
non-zero digit to the left of the decimalnon-zero digit to the left of the decimal
point.point.
 Count the number of decimal places theCount the number of decimal places the
decimal point has “moved” from thedecimal point has “moved” from the
original number. This will be the exponentoriginal number. This will be the exponent
on the 10.on the 10.
 If the original number was less than 1, thenIf the original number was less than 1, then
the exponent is negative. If the originalthe exponent is negative. If the original
number was greater than 1, then thenumber was greater than 1, then the
exponent is positive.exponent is positive.

47. +

48. +
TRY…
Express in Scientific Notation
1. 230
2. 14 100 000
3. 0.00026
4. 0.000000698
5. 0.089

49. +
Change Scientific Notation back to
Standard Form
 Simply move the decimal point to the right for positiveSimply move the decimal point to the right for positive
exponent 10.exponent 10.
 Move the decimal point to the left for negative exponent 10.Move the decimal point to the left for negative exponent 10.
(Use zeros to fill in places.)(Use zeros to fill in places.)
 Example:Example:
 Given: 5.093 x 10Given: 5.093 x 1066
 Move: 6 places to the right (positive)Move: 6 places to the right (positive)
 Answer: 5,093,000Answer: 5,093,000

50. +
TRY…
Express in Standard Notation
1. 1.5 x 103
2. 3.4 x 108
3. 6.86 x 10-6
4. 5.822 x 10-5
5. 4.02 x 1010

51. +
OPERATIONS WITH SCIENTIFIC
NOTATION

52. +
TRY…

53. +
OPERATIONS WITH SCIENTIFIC
NOTATION

54. +
OPERATIONS WITH SCIENTIFIC
NOTATION

55. +
TRY…

56. +
SIGNIFICANT FIGURES
Number of significant digits that
implies the accuracy of
measurement

57. +
Determining the number of
significant figures
Rules:
1.All nonzero digits are significant.
25 L – 2 significant figures
65.2 kg – 3 significant figures

58. 2. Zeros between two nonzero digits
are significant.
29.05 g – 4 significant figures
1.0087 mL – 5 significant figures

59. 3. Leading zeros are not
significant.
0.000000872 miles – 3
significant figures
0.03 mg – 1 significant figure

60. 4. Trailing zeros in a number containing a
decimal point are significant
25.70 lbs – 4 significant figures
708.00 km – 5 significant figures

61. 5. The trailing zeros in which decimal point
is not given/placed indicated that zero/s
is/are not significant.
1, 245, 500 m – 5 significant figures
5280 ft – 3 significant figures

62. +
TRY…
How many significant figures do each
number contain?
1.34.08 L
2.0.0054 mm
3.260.00 g
4.550 miles
5.0.008 mL

63. 6. 3.7500 cm
7. 1,200,000
miles
8. 23.45 lbs
9. 1, 000, 0034 ft
10. 0.001003 mm

64. +
RULES FOR USING SIGNIFICANT
FIGURES IN CALCULATIONS
When adding or subtracting
significant figures, the answer
should have the same number of
decimal places as the original
number with the fewest decimal
places.

65. + Example:
Baby Zayn weighed 3.6 kg at birth and
10.11 kg on his first birthday. How much
weight did he gain in his first year of life.
10.11 kg
- 3.6 kg
6. 51 kg
•The answer can have only one digit after
the decimal point.
•Round 6.51 to 6.5
•Baby Zayn gained 6.5 kg during his first
year of life.

66. +
RULES FOR USING SIGNIFICANT
FIGURES IN CALCULATIONS
When multiplying or dividing
significant figures, the answer
should have the same number of
significant figures as the original
number with the fewest significant
figures.

67. +
TRY…
Solve the following and write you
answer in correct significant
figure.
1. 8.937 + 8.930=
2. 0.00015 x 54.6=
3. 847.89 - 847.73=
4. 3.2 / 1.60 =
5. 7.1 x 10=